Non-implication réciproque
En logique, la non-implication réciproque[1] est un connecteur logique qui est la négation de la réciproque de l'implication.
Définition
, qui est la même que
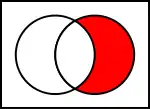
Diagramme de Venn
Le diagramme de Venn de « Il n'est pas vrai que B implique A » (la zone rouge est vraie).
Toujours en rapport avec le complémentaire, où le complémentaire de A dans B est notée B ∖ A.
Propriétés
Préservation du faux: L'interprétation sous laquelle toutes les variables sont affectées de la valeur de vérité «faux» produit une valeur de vérité de «faux» à la suite de l'application de la non-implication réciproque.
Symbole
Les alternatives de sont
- : combine la flèche gauche de l'implication réciproque () avec le tilde de la négation ().
- : utilise la lettre majuscule M préfixé.
- : combine la flèche gauche de l'implication réciproque () nié au moyen d'une barre ().
Langage naturel
Rhétorique
« non A mais B »
Algèbre de Boole
La non-implication réciproque dans une algèbre booléenne générale est définie comme .
Exemple d'une algèbre booléenne à 2 éléments: les 2 éléments {0,1}, les opérateurs comme opérateur complémentaire, comme opérateur de jointure et en tant qu'opérateur de rencontre, construisent l'algèbre de Boole de la logique propositionnelle.
|
|
et |
|
et |
|
alors signifie |
| |||||||||||||||||||||||||||||||||||||||
| (Négation) | (Ou Inclusif) | (Et) | (Non-implication réciproque) |
Exemple d'une algèbre booléenne à 4 éléments: les 4 diviseurs {1,2,3,6} de 6 avec 1 nul et 6 en tant qu'élément d'unité, les opérateurs (co-diviseur de 6) comme opérateur complémentaire, (plus grand diviseur commun) construisent une algèbre de Boole.
|
|
et |
|
et |
|
alors signifie |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (Co-diviseur de 6) | (Plus Petit Diviseur Commun) | (Plus Grand Diviseur Commun) | (Plus grand diviseur x premier avec y) |
Informatique
Un exemple pour de non-implication réciproque en informatique peut être trouvé lors d'une jointure externe droite sur un ensemble de tables d'une base de données, si les enregistrements ne correspondant pas au-condition de jointure de la table « gauche » sont exclus[3].
Notes
- Lehtonen, Eero, and Poikonen, J.H.
- Knuth 2011, p. 49
- Jeff Atwood, « A Visual Explanation of SQL Joins », sur codinghorror.com, (consulté le ).
Références
- (en) Donald E. Knuth, The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1, Addison-Wesley Professional, (ISBN 0-201-03804-8)


























