Accueil🇫🇷Chercher

Nombre de Thue

Dans le domaine mathématique de la théorie des graphes, le nombre de Thue d'un graphe est une variante de l'indice chromatique, définie par Alon et ses coauteurs en 2002[1], et appelée du nom du mathématicien Axel Thue, qui a étudié les mots sans carrés utilisés pour définir ce nombre.

Le nombre de Thue du cycle de longueur 5 est quatre.

Définition

Une coloration non répétitive d'un graphe est une affectation de couleurs aux arêtes du graphe telle qu'il n'existe pas de chaîne longueur paire dans laquelle les couleurs des arêtes dans la première moitié de la chaîne forment la même suite que les couleurs des arêtes de la seconde moitié de la chaîne. Le nombre de Thue d'un graphe est le nombre minimum de couleurs nécessaires dans une coloration non répétitive.

Au lieu de la coloration des arêtes, on peut considérer la coloration des sommets d'un graphe, par des couleurs ou des listes de couleurs. On appelle nombre chromatique non répétitif le plus petit nombre de couleurs nécessaires pour colorer les sommets d'un graphe de sorte que les couleurs des sommets de toute chaîne sont sans facteur carré. Fiorenzi, Ochem et al.[2] étudient des listes de couleurs pour les arbres.

Des variations de ces notions ont été étudiées dans plusieurs articles, notamment de Barát et Varjú[3] (2008), Barát et Wood[4] (2005), Brešar et Klavžar[5] (2004), et Kündgen et Pelsmajer[6] (2008). Un article de synthèse des premiers résultats a été publié par Jaroslaw Grytczuk en 2007[7]. Une autre bibliographie détaillée est donnée par Dujmović, Esperet et al. [8].

Exemple

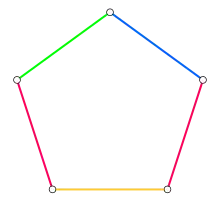
Un pentagone est un cycle de cinq sommets noté C 5. Si on colorie ses arêtes avec deux couleurs, il y a deux arêtes adjacentes avec la même couleur x ; le chemin formé par ces deux arêtes est la suite de couleurs répétitive xx. Si on utilise trois couleurs, l'une des trois couleurs n'est utilisée qu'une seule fois ; le chemin de quatre arêtes formé par les arêtes des deux autres couleurs a soit deux arêtes consécutives de même couleur, soit donne la séquence de couleurs répétées xyxy. Cependant, avec quatre couleurs, il n'est pas difficile d'éviter toute répétition. Par conséquent le nombre de Thue de C 5 est quatre.

Résultats

Alon et al.[1] utilisent le lemme local de Lovász pour prouver que le nombre de Thue de tout graphe est majoré par le carré de son degré maximum ; ils fournissent un exemple montrant que pour certains graphes, cette majoration quadratique est atteinte. De plus, ils montrent que le nombre de Thue de toute chaîne de longueur au moins quatre est exactement trois, que le nombre de Thue de tout cycle est au plus quatre, et que le nombre de Thue du graphe de Petersen est exactement cinq.

Cycles

Les cycles dont on sait que le nombre de Thue est quatre sont C 5, C 7, C 9, C 10, C 14 et C 17 . Alon et al.[1] ont conjecturé que le nombre de Thue de tout cycle plus long est trois. Currie a résolu cette conjecture en 2002[9] en montrant que tous les cycles avec 18 sommets ou plus ont le nombre de Thue 3.

Graphes planaires

La recherche d'une majoration du nombre de Thue des graphes planaires a abouti en 2020 à un article de Dujmović, Esperet et al. [8] ; ils résolvent une conjecture déjà formulée par Grytczuk[7] et montrent que le nombre de Thue des graphes planaires est borné ; plus précisément, ils montrent que le nombre de Thue de tout graphe planaire est au plus 768. Ils donnent aussi des majorations pour d'autres classes plus générales, les graphes de genre borné, les graphes excluant un mineur excluant un mineur fixe, et les graphes excluant un mineur topologique fixe. Ainso, ils montrent que tout graphe de genre g a un nombre de Thue majoré par 256 max(2g,3), et que pour tout graphe X, il existe un entier k tel que tout graphe à mineur X exclua un nombre de Thue majoré par k.

Coloration des sommets

Plusieurs classes de graphes ont un nombre chromatique non répétitif bornés[8]. En particulier, les cycles sont non répétitivement 3-colorables (sauf pour un nombre fini d'exceptions[9]) , les arbres sont non répétitivement 4-colorables[10] - [6], les graphes planaires extérieurs sont non répétitivement 12-colorables[3] - [6], et plus généralement, tout graphe de largeur arborescente est non répétitivement -colorable[3]. Les graphes de degré maximal ∆ sont non répétitivement -colorables[1] - [11] - [12] - [7] - [13] ; les graphes qui excluent une immersion fixe ont un nombre chromatique non répétitif borné[14].

Complexité de calcul

Tester si une coloration possède un chemin répétitif est dans la classe NP, donc tester si une coloration est non répétitive est en co-NP, et Fedor Manin[15] a montré que le problème est co-NP-complet. Le problème de trouver une telle coloration appartient à dans la hiérarchie polynomiale, et à nouveau Manin a montré qu'il est complet pour ce niveau[16].

Notes et références
  1. Noga Alon, Jaroslaw Grytczuk, Mariusz Hałuszczak et Oliver Riordan, « Nonrepetitive colorings of graphs », Random Structures and Algorithms, vol. 21, nos 3-4,‎ , p. 336-346 (DOI 10.1002/rsa.10057, MR 1945373, lire en ligne).
  2. Francesca Fiorenzi, Pascal Ochem, Patrice Ossona de Mendez et Xuding Zhu, « Thue choosability of trees », Discrete Applied Mathematics, vol. 159, no 17,‎ , p. 2045–2049 (ISSN 0166-218X, DOI 10.1016/j.dam.2011.07.017).
  3. János Barát et Péter P. Varjú, « On square-free edge colorings of graphs », Ars Combinatoria, vol. 87,‎ , p. 377–383 (MR 2414029, lire en ligne).
  4. János Barát et David Wood, « Notes on nonrepetitive graph colouring », Electronic Journal of Combinatorics, vol. 15, no 1,‎ (MR 2426162, arXiv math.CO/0509608).
  5. Boštjan Brešar et Sandi Klavžar, « Square-free coloring of graphs », Ars Combinatoria, vol. 70,‎ , p. 3–13 (MR 2023057).
  6. André Kündgen et Michael J. Pelsmajer, « Nonrepetitive colorings of graphs of bounded tree-width », Discrete Mathematics, vol. 308, no 19,‎ , p. 4473–4478 (DOI 10.1016/j.disc.2007.08.043, MR 2433774).
  7. Jarosław Grytczuk, « Nonrepetitive colorings of graphs — a survey », International Journal of Mathematics and Mathematical Sciences,‎ , article no 74639 (MR 2272338, lire en ligne).
  8. Vida Dujmović, Louis Esperet, Gwenaël Joret, Bartosz Walczak et David Wood, « Planar graphs have bounded nonrepetitive chromatic number », Advances in Combinatorics,‎ (ISSN 2517-5599, DOI 10.19086/aic.12100, arXiv 1904.05269).
  9. James D. Currie, « There are ternary circular square-free words of length n for n ≥ 18 », Electronic Journal of Combinatorics, vol. 9, no 1,‎ (MR 1936865, lire en ligne).
  10. B. Brešar, J. Grytczuk, S. Klavžar, S. Niwczyk et I. Peterin, « Nonrepetitive colorings of trees », Discrete Mathematics, vol. 307, no 2,‎ , p. 163–172 (DOI 10.1016/j.disc.2006.06.017)
  11. Vida Dujmović, Gwenaël Joret, Jakub Kozik et David R. Wood, « Nonrepetitive colouring via entropy compression », Combinatorica, vol. 36, no 6,‎ , p. 661–686 (ISSN 0209-9683, DOI 10.1007/s00493-015-3070-6)
  12. Martin Grohe et Dániel Marx, « Structure Theorem and Isomorphism Test for Graphs with Excluded Topological Subgraphs », SIAM Journal on Computing, vol. 44, no 1,‎ , p. 114–159 (ISSN 0097-5397, DOI 10.1137/120892234)
  13. Jochen Harant et Stanislav Jendrol’, « Nonrepetitive vertex colorings of graphs », Discrete Mathematics, vol. 312, no 2,‎ , p. 374–380 (ISSN 0012-365X, DOI 10.1016/j.disc.2011.09.027).
  14. Paul Wollan et David R. Wood, « Nonrepetitive colorings of graphs excluding a fixed immersion or topological minor », Journal of Graph Theory, vol. 91, no 3,‎ , p. 259–266 (ISSN 0364-9024, DOI 10.1002/jgt.22430).
  15. Fedor Manin, « The complexity of nonrepetitive edge coloring of graphs », Arxiv,‎ (arXiv 0709.4497).
  16. Marcus Schaefer et Christopher Umans, « Completeness in the polynomial-time hierarchy: a compendium », Preprint,‎ (lire en ligne).

Liens externes
    Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.