Moyenne logarithmique
En mathématiques, la moyenne logarithmique est un type de moyenne.
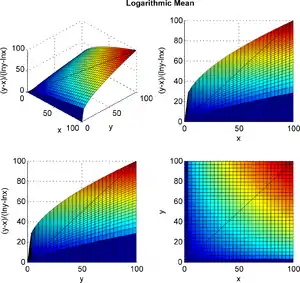
Pour deux réels strictement positifs, elle est égale à leur différence, divisée par le logarithme de leur quotient. Cette moyenne est utilisée lors de problèmes d'ingénierie concernant le transfert de chaleur et de masse.
Définition
La moyenne logarithmique de deux réels strictement positifs est définie par :
- .
Ainsi, par exemple, la moyenne logarithmique de 1 et 2 est , voir la suite A007525 de l'OEIS.
Propriétés
La moyenne logarithmique est bien une moyenne, car comprise entre a et b (ce résultat est connu sous le nom d'« inégalité de Napier[1]»). Elle est de plus homogène : .
Inégalités
La moyenne logarithmique de deux nombres est inférieure ou égale à leur moyenne arithmétique et à leur moyenne d'ordre 1/2 , mais supérieure ou égale à leur moyenne géométrique et à leur moyenne harmonique ; plus précisément :
Les deux inégalités extrêmes viennent de la croissance avec de la moyenne d'ordre et les deux inégalités centrales de la croissance avec de la moyenne de Stolarsky .
Ces deux dernières inégalités se démontrent élémentairement comme suit.
Pour , on pose ; les inégalités s'écrivent alors .
En remplaçant par , la première inégalité s'écrit , inégalité classique.
La deuxième s'écrit aussi ; en remplaçant par , elle s'écrit , inégalité également classique.
Diverses obtentions de cette moyenne
Par le théorème des accroissements finis
D'après le théorème des accroissements finis, il existe un réel entre a et b où la dérivée d'une fonction f est égale à la pente de la sécante :
La moyenne logarithmique est le nombre lorsque l'on prend :
soit :
Par intégration
La moyenne logarithmique peut également être interprétée comme l'aire sous une courbe définie par des fonctions exponentielle :
Carlson donne d'autres expressions intégrales[5]:
D'après le théorème des sommes de Riemann, est la limite de la suite décroissante , formée de moyennes arithmétiques de moyennes géométriques pondérées.
Généralisation
Par le théorème des accroissements finis généralisé à l'ordre n
On peut généraliser la moyenne logarithmique à n + 1 variables en considérant le théorème des accroissements finis généralisé à l'ordre n faisant intervenir les différences divisées d'ordre n du logarithme.
On obtient
où désigne la différence divisée d'ordre n du logarithme.
Pour n = 2, cela donne par exemple :
- .
Par intégration
L'interprétation intégrale peut aussi être généralisée à plusieurs variables, mais elle conduit à un résultat différent. Étant donné le simplexe où et une mesure appropriée qui assigne au simplexe un volume égal à 1, on obtient
Cela peut être simplifié en utilisant les différences divisées de la fonction exponentielle pour
- .
Exemple pour
- .
Voir également
- La moyenne géométrique, autre moyenne liée aux logarithmes
- La moyenne de Stolarsky dont la moyenne logarithmique est un cas particulier
- Différence de température moyenne logarithmique (en)
Références
- Notes
- (en) Eric W. Weisstein, « Napier's Inéquality », sur MathWorld
- (en) B. C. Carlson, « Some inequalities for hypergeometric functions », Proc. Amer. Math. Soc., vol. 17, , p. 32–39 (DOI 10.1090/s0002-9939-1966-0188497-6)
- (en) B. Ostle et H. L. Terwilliger, « A comparison of two means », Proc. Montana Acad. Sci., vol. 17, , p. 69–70
- (en) Tung-Po Lin, « The Power Mean and the Logarithmic Mean », The American Mathematical Monthly, vol. 81, (DOI 10.1080/00029890.1974.11993684)
- (en) Billie C. Carlson, « The Logarithmic Mean », The American Mathematical Monthly, vol. 79, no 6, , p. 615– (DOI 10.2307/2317088)
- Bibliographie
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Logarithmic mean » (voir la liste des auteurs).

![{\displaystyle {\begin{aligned}M_{\text{ln}}(a,b)&=\lim _{(x,y)\to (a,b)}{\frac {x-y}{\ln x-\ln y}}\\[6pt]&={\begin{cases}a&{\text{si }}a=b,\\{\frac {b-a}{\ln b-\ln a}}&{\text{sinon}}\end{cases}}\end{aligned}}}](https://img.franco.wiki/i/2221c15d7c805eaebb1f58839a9bd9075a69740c.svg)
















![{\displaystyle \exists c\in ]a,b[:\ f'(c)={\frac {f(b)-f(a)}{b-a}}}](https://img.franco.wiki/i/5d0e6b7939f33c9612b5c8f9dd66666dea391c02.svg)




![{\displaystyle \int _{0}^{1}a^{1-t}b^{t}\ \mathrm {d} t=a\int _{0}^{1}\left({\frac {b}{a}}\right)^{t}\mathrm {d} t=a\left[{\frac {1}{\ln \left({\frac {b}{a}}\right)}}\left({\frac {b}{a}}\right)^{t}\right]_{t=0}^{t=1}={\frac {b-a}{\ln \left({\frac {b}{a}}\right)}}={\frac {b-a}{\ln b-\ln a}}}](https://img.franco.wiki/i/4b5e84556dd3437883233b7dc4eb567b897ef6c3.svg)


![{\displaystyle \int _{0}^{\infty }{\operatorname {d} \!t \over (t+a)\,(t+b)}={1 \over b-a}\int _{0}^{\infty }\left({1 \over (t+a)}-{1 \over (t+b)}\right)\operatorname {d} \!t={1 \over b-a}\left[\ln \left({{t+a} \over t+b}\right)\right]_{0}^{\infty }={\frac {-\ln(a/b)}{b-a}}}](https://img.franco.wiki/i/a79c57246e391d5a8c43e569380e30c961a81154.svg)

![{\displaystyle \left({\frac {1}{n+1}}\displaystyle \sum _{k=0}^{n}{\sqrt[{n}]{a^{n-k}b^{k}}}\right)_{n\geqslant 0}}](https://img.franco.wiki/i/4b582ca24961e483c5420582564f9a4cfcccf745.svg)
![{\displaystyle L_{\text{MV}}(x_{0},\,\dots ,\,x_{n})={\sqrt[{-n}]{(-1)^{(n+1)}n\ln \left(\left[x_{0},\,\dots ,\,x_{n}\right]\right)}}}](https://img.franco.wiki/i/a3f768d4332d13acc1ed2bef32032c7fd92c84bc.svg)
![{\displaystyle \ln \left(\left[x_{0},\,\dots ,\,x_{n}\right]\right)}](https://img.franco.wiki/i/7456e6367275d5f13829e0150ea009b5b093bb38.svg)
![{\displaystyle L_{\text{MV}}(x,y,z)={\sqrt {\frac {(x-y)\left(y-z\right)\left(z-x\right)}{2\left[\left(y-z\right)\ln x+\left(z-x\right)\ln y+\left(x-y\right)\ln z\right]}}}}](https://img.franco.wiki/i/db8cfd5f60e635198611cab3630da306f1bbadd0.svg)




![{\displaystyle L_{\text{I}}\left(x_{0},\,\dots ,\,x_{n}\right)=n!\exp \left[\ln \left(x_{0}\right),\,\dots ,\,\ln \left(x_{n}\right)\right]}](https://img.franco.wiki/i/a0beb3a5bfda4ba6e6185d83ddf13c718d7a590c.svg)




