En mathématiques, la moyenne de Lehmer d'une famille  de nombres réels strictement positifs, portant le nom de Derrick Henry Lehmer, est une moyenne définie par [2]:
de nombres réels strictement positifs, portant le nom de Derrick Henry Lehmer, est une moyenne définie par [2]:

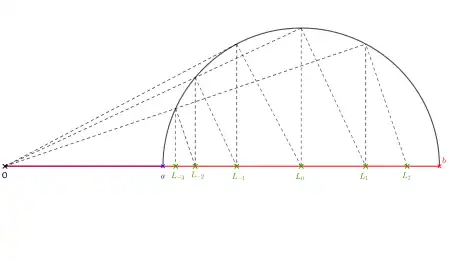
Construction géométrique des moyennes de Lehmer de deux nombres réels, selon un résultat de Farnsworth et Orr
[1].
où p est un réel quelconque.
La moyenne de Lehmer pondérée par une famille  de poids positifs est définie par :
de poids positifs est définie par :

Elle n'est autre que la moyenne de  pondérée par la famille
pondérée par la famille  .
.
La moyenne de Lehmer propose une alternative à la moyenne de Hölder habituelle pour relier le minimum et le maximum en passant par la moyenne harmonique et la moyenne arithmétique.
Propriétés
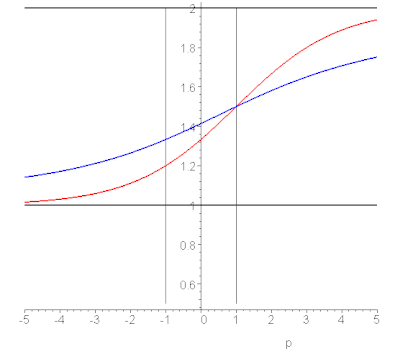
Comparaison entre la moyenne de Lehmer

de 1 et 2 (en rouge), avec leur moyenne de Hölder

(en bleu).
La moyenne de Lehmer d'ordre p + 1 d'un n-uplet de nombres positifs est supérieure ou égale à la moyenne (de Hölder) d'ordre p si et seulement si p est supérieur ou égal à 1, et inversement [3]:

La moyenne de Lehmer ne respecte pas l'inégalité de Minkowski pour tout ordre[3]:

La dérivée de 
![{\displaystyle {\frac {\partial }{\partial p}}L_{p}(x_{1},\cdots ,x_{n})={\frac {\left(\sum _{j=1}^{n}\sum _{k=j+1}^{n}\left[x_{j}-x_{k}\right]\cdot \left[\ln(x_{j})-\ln(x_{k})\right]\cdot \left[x_{j}\cdot x_{k}\right]^{p-1}\right)}{\left(\sum _{k=1}^{n}x_{k}^{p-1}\right)^{2}}},}](https://img.franco.wiki/i/bfd35a2c378f6ee65fa8c5e92f087ef0b15f40d9.svg)
étant positive, cette fonction est croissante ; on a donc l’implication

La dérivée de la moyenne pondérée de Lehmer est :













![{\displaystyle {\frac {\partial }{\partial p}}L_{p}(x_{1},\cdots ,x_{n})={\frac {\left(\sum _{j=1}^{n}\sum _{k=j+1}^{n}\left[x_{j}-x_{k}\right]\cdot \left[\ln(x_{j})-\ln(x_{k})\right]\cdot \left[x_{j}\cdot x_{k}\right]^{p-1}\right)}{\left(\sum _{k=1}^{n}x_{k}^{p-1}\right)^{2}}},}](https://img.franco.wiki/i/bfd35a2c378f6ee65fa8c5e92f087ef0b15f40d9.svg)










