Moitié bipartie

En théorie des graphes, la moitié bipartie ou le demi-carré d'un graphe biparti ${\displaystyle G=(U,V,E)}$ est un graphe ${\displaystyle H=(U,F)}$ dont l'ensemble des sommets est l'ensemble ${\displaystyle U}$ (l'un des deux ensembles des sommets de la bipartition) et dans lequel il y a une arête ${\displaystyle (u,u')}$ entre ${\displaystyle u}$ et ${\displaystyle u'}$ s'ils sont à distance deux dans ${\displaystyle G}$[1], en d'autres termes, s'il existe un sommet ${\displaystyle v\in V}$ tel qu'il existe une arête entre ${\displaystyle u}$ et ${\displaystyle v}$ et entre ${\displaystyle u'}$ et ${\displaystyle v}$ dans le graphe ${\displaystyle G}$. Dans une notation plus compacte, la moitié bipartie est ${\displaystyle H=G^{2}(U)}$, où l'exposant dénote le carré du graphe et l'ensemble entre crochets dénote le sous-graphe induit par ${\displaystyle U}$.

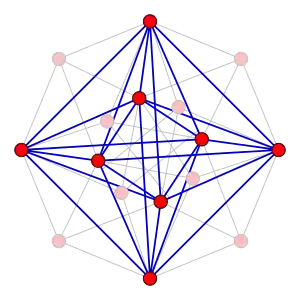
Par exemple, le demi-carré du graphe biparti complet ${\displaystyle K_{n,n}}$ est le graphe complet ${\displaystyle K_{n}}$K_n et la moité biparti de l'hypercube est le demi-hypercube. Quand ${\displaystyle G}$ est un graphe distance-régulier, ses deux moitiés biparties sont des graphes distance-réguliers[2].

Par exemple, la moitié bipartie du graphe de Foster est l'un des graphes de la famille finie des graphes distance-réguliers localement linéaires (en) de degré 6[3].

Les « Map graphs » qui sont les graphes d'intersection de régions simplement connexes du plan d'intérieurs disjoints, sont exactement les moitiés biparties de graphes planaires[4]

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.