Modulateur acousto-optique
Un modulateur acousto-optique (MAO, ou AOM en anglais, pour acousto-optic modulator), également appelé cellule de Bragg, utilise l’effet acousto-optique pour diffracter et changer la fréquence de la lumière par ondes sonores (généralement proche des fréquences radio). Il est utilisé dans les lasers pour la commutation-Q, en télécommunication pour effectuer de la modulation du signal, et en spectroscopie pour du contrôle de fréquence.
Historique
La possibilité d'interaction entre ondes acoustiques et lumière est prédite par Léon Brillouin en 1922[1]
Principe de fonctionnement
La propagation de l'onde acoustique dans le milieu se traduit par des variations de pression dans le milieu et donc par des variations d'indice (optique) du milieu[2].
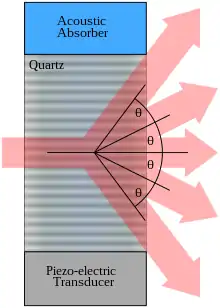
Un oscillateur piézo-électrique est relié à un matériau, par exemple du verre. Un signal électrique oscillant force la cellule piézo-électrique à vibrer, ce qui crée des ondes sonores dans le verre. Ceci peut être imaginé comme des plans de dilatation et de compression, se déplaçant périodiquement, et venant changer l’indice de réfraction. La lumière entrante est dispersée (voir dispersion de Brillouin) en dehors de la modulation périodique de l’indice résultante, et une interférence a lieu, similaire à celle créée lors d’une diffraction de Bragg. L’interaction peut être pensée comme le mélange de quatre ondes entre phonons et photons.
Propriétés
La totalité des informations reportées ci-après sont valables pour un fonctionnement optimal du modulateur. Le fonctionnement optimal du MAO est effectif dans le cas où l'angle entre l'axe de passage du modulateur et l'axe du faisceau entrant est égal à l'angle de Bragg. Cet angle est caractéristique de chaque modulateur acousto-optique, habituellement de l'ordre de quelques milliradians. Dans ce cas, les propriétés de la lumière sortant du MAO peuvent être contrôlées suivant cinq paramètres :
Déflexion
- Un rayon diffracté ressort avec un angle θ qui dépend du rapport entre la longueur d’onde de la lumière λ et la longueur d’onde du son Λ.
- Avec m = …-2,-1,0,1,2,… l’ordre de diffraction. La diffraction à modulation sinusoïdale dans un petit cristal entraîne les ordres de diffraction m = -1,0,1. Des diffractions en cascade à travers des cristaux d’épaisseur moyenne créent des ordres de diffraction supérieurs. Dans des cristaux épais, à faible modulation, seuls les ordres de fréquence correspondante sont diffractés : on l’appelle alors diffraction de Bragg. La déflexion angulaire varie de 1 à 5000 fois la largeur du rayon (le nombre de points de résolution). Par conséquent, la déflexion est généralement limitée à quelques dixièmes de milliradians.
- On a habituellement un angle de déflexion sur l'ordre 1 deux fois plus élevé que l'angle de Bragg s'il est appliqué en entrée du modulateur.
Intensité
- La quantité de lumière diffractée par l’onde sonore dépend de l’intensité du son. Par conséquent, l’intensité du son peut être utilisée pour moduler l’intensité de la lumière dans le rayon diffracté. Typiquement, l’intensité qui est diffractée pour un ordre m = 0 peut varier entre 15 et 99 % de l’intensité lumineuse d’entrée. De même, l’intensité pour un ordre m = 1 peut varier entre 0 et 90 %.
Fréquence
- À la différence de la diffraction de Bragg, la lumière est diffusée à partir de plans mobiles. Par conséquent, la fréquence d’un rayon diffractée f à l’ordre m doit être corrigée par une quantité proportionnelle à la fréquence de l’onde sonore F (effet Doppler).
- Ce changement de fréquence est nécessaire comme l’exige la loi de la conservation de l’énergie et de la quantité de mouvement (pour les photons et les phonons) pendant le processus. Les valeurs traditionnelles de changement de fréquence peuvent varier entre la dizaine de MHz et 1,5 GHz. Dans certains MAO, deux ondes acoustiques voyagent dans des directions opposées au sein du matériau, formant une onde stationnaire. La diffraction à partir de l’onde stationnaire ne change pas la fréquence de la lumière diffractée.
Phase
- La phase du rayon diffracté va être elle aussi modifiée par la phase de l’onde sonore. La phase peut être changée d'une valeur arbitraire.
Polarisation
- Les ondes acoustiques transversales colinéaires ou les ondes longitudinales perpendiculaires peuvent changer de polarisation. Les ondes acoustiques induisent un changement de phase biréfringent, de la même manière que dans une cellule de Pockels. Les filtres acousto-optiques variables, en particulier le « dazzler » qui peut générer des formes de pulsation variables, sont basés sur ce principe.
Les modulateurs acousto-optiques sont plus rapides que leurs homologues mécaniques, comme les miroirs basculants. Le temps que prend un MAO pour modifier le rayon sortant est limité par le temps de transit de l’onde sonore à travers le rayon (généralement compris entre 5 et 100 nanosecondes). C’est suffisamment rapide pour autoriser le verrouillage de mode actif dans un laser ultra-rapide. Quand un contrôle plus rapide est nécessaire, on utilise alors des modulateurs électro-optiques. Il faut cependant les alimenter avec des fortes tensions (de l’ordre de 10 kilovolts), alors que les MAO offrent une plage de déflexion plus grande, sont d’une conception simple, et consomment peu de puissance (inférieure à 3 watts).

