Misty1
Misty1 (pour «Mitsubishi Improved Security Technology») a été créé en 1995 par Mitsuru Matsui pour Mitsubishi Electric(en)_[https://web.archive.org/web/20000823133547/http://www.mitsubishi.com/ghp_japan/misty/misty_e_b.pdf_rapport_technique]_2-0">[2].
| Concepteur(s) | Mitsuru Matsui |
|---|---|
| Première publication | 1995 |
| Dérivé de | Aucun |
| Chiffrement(s) basé(s) sur cet algorithme | Camellia, MISTY2, KASUMI |
| Taille(s) du bloc | 64 bits |
|---|---|
| Longueur(s) de la clé | 128 bits |
| Structure | réseau de Feistel |
| Nombre de tours | 8 tours |
Meilleure cryptanalyse
Une attaque complète avec recouvrement total de la clef en 263,9999 chiffrés choisis et en temps 279 ou en 264 chiffrés choisis et en temps 269.5 opérations[1]
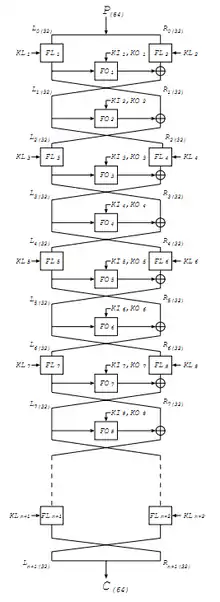
Misty1 est un algorithme de chiffrement symétrique par blocs de 64 bits avec une clé de 128 bits et un nombre variable de tours, basé sur un réseau de Feistel. Misty1 est conçu pour résister à la cryptanalyse différentielle et à la cryptanalyse linéaire, et pour être très rapide dans ses mises en œuvre matérielles et logicielles. Il est recommandé d'utiliser Misty1 avec huit tours pour un bon compromis vitesse/sécurité.
Description de l'algorithme
L'algorithme peut être divisé en deux parties, à savoir la gestion de la clé et le chiffrement/déchiffrement à proprement parler.
Terminologie
Les opérateurs suivants sont utilisés pour décrire l'algorithme :
- l'opérateur + pour l'addition en complément à deux
- l'opérateur * pour la multiplication
- l'opérateur / pour le quotient de la division euclidienne
- l'opérateur % pour le reste de la division euclidienne
- l'opérateur & pour le et binaire
- l'opérateur | pour le ou binaire
- l'opérateur ^ pour le ou exclusif ou XOR binaire
- l'opérateur << pour le décalage d'un bit vers la gauche
- l'opérateur >> pour le décalage d'un bit vers la droite
Gestion de la clé
L'expansion de la clé est réalisé par l'algorithme suivant :
pour i = 0, etc., 7 faire
EK[i] = K[i*2]*256 + K[i*2+1]
finpour pour i = 0, etc., 7 faire
EK[i+ 8] = FI(EK[i], EK[(i+1)%8])
EK[i+16] = EK[i+8] & 0x1ff
EK[i+24] = EK[i+8] >> 9 finpour
K est la clé secrète de 128 bits et chaque octet de K est noté K[i].
EK est la clé étendue et chaque élément de EK représente deux octets et est noté EK[i].
K[0 .. 15] est copié dans EK[0 .. 7] puis l'extension de la clé est produite à partir de EK[0 .. 7] en utilisant la fonction FI (décrite dans la section suivante) et est stocké dans EK[8 .. 15].
Le chiffrement
Cette partie décrit les deux fonctions utilisée pour le chiffrement : FO et FL.
La fonction FO utilise (comme l'expansion de la clé ci-dessus) la sous-routine FI. La sous-routine FI utilise deux boîtes-S (S-BOXES) à savoir S7 et S9.
La fonction FO
La fonction FO prend deux paramètres. Le premier est une entrée de 32 bits nommée FO_IN, l'autre est un index d'EK noté k. FO renvoie un buffer de 32 bits de données nommé FO_OUT (ceci est dû à sa structure de schéma de Feistel sur 64 bits).
fonction FO(FO_IN, k)
variables t0, t1 (entiers de 16 bits)
début
t0 = FO_IN >> 16
t1 = FO_IN & 0xffff
t0 = t0 ^ EK[k]
t0 = FI(t0, EK[(k+5)%8+8])
t0 = t0 ^ t1
t1 = t1 ^ EK[(k+2)%8]
t1 = FI(t1, EK[(k+1)%8+8])
t1 = t1 ^ t0
t0 = t0 ^ EK[(k+7)%8]
t0 = FI(t0, EK[(k+3)%8+8])
t0 = t0 ^ t1
t1 = t1 ^ EK[(k+4)%8]
FO_OUT = (t1<<16) | t0
retourner FO_OUT
fin
La fonction FI
La fonction FI prend deux paramètres. Le premier est une entrée de 16 bits nommée FI_IN, l'autre est une partie d'EK de 16 bits, à savoir FI_KEY. FI renvoie un buffer de 16 bits, FI_OUT. La fonction FI effectue une substitution d'octet non linéaire par boîte-S.
fonction FI(FI_IN, FI_KEY)
variable d9 (entier de 9 bits)
variable d7 (entier de 7 bits)
début
d9 = FI_IN >> 7
d7 = FI_IN & 0x7f
d9 = S9[d9] ^ d7
d7 = S7[d7] ^ d9
(d7 = d7 & 0x7f)
d7 = d7 ^ (FI_KEY >> 9)
d9 = d9 ^ (FI_KEY & 0x1ff)
d9 = S9[d9] ^ d7
FI_OUT = (d7<<9) | d9
retourner FI_OUT
fin
Voici la description des tables S7 et S9 en notation hexadécimale :
| S7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f |
| 00: | 1b | 32 | 33 | 5a | 3b | 10 | 17 | 54 | 5b | 1a | 72 | 73 | 6b | 2c | 66 | 49 |
| 10: | 1f | 24 | 13 | 6c | 37 | 2e | 3f | 4a | 5d | 0f | 40 | 56 | 25 | 51 | 1c | 04 |
| 20: | 0b | 46 | 20 | 0d | 7b | 35 | 44 | 42 | 2b | 1e | 41 | 14 | 4b | 79 | 15 | 6f |
| 30: | 0e | 55 | 09 | 36 | 74 | 0c | 67 | 53 | 28 | 0a | 7e | 38 | 02 | 07 | 60 | 29 |
| 40: | 19 | 12 | 65 | 2f | 30 | 39 | 08 | 68 | 5f | 78 | 2a | 4c | 64 | 45 | 75 | 3d |
| 50: | 59 | 48 | 03 | 57 | 7c | 4f | 62 | 3c | 1d | 21 | 5e | 27 | 6a | 70 | 4d | 3a |
| 60: | 01 | 6d | 6e | 63 | 18 | 77 | 23 | 05 | 26 | 76 | 00 | 31 | 2d | 7a | 7f | 61 |
| 70: | 50 | 22 | 11 | 06 | 47 | 16 | 52 | 4e | 71 | 3e | 69 | 43 | 34 | 5c | 58 | 7d |
| S9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f |
| 000: | 1c3 | 0cb | 153 | 19f | 1e3 | 0e9 | 0fb | 035 | 181 | 0b9 | 117 | 1eb | 133 | 009 | 02d | 0d3 |
| 010: | 0c7 | 14a | 037 | 07e | 0eb | 164 | 193 | 1d8 | 0a3 | 11e | 055 | 02c | 01d | 1a2 | 163 | 118 |
| 020: | 14b | 152 | 1d2 | 00f | 02b | 030 | 13a | 0e5 | 111 | 138 | 18e | 063 | 0e3 | 0c8 | 1f4 | 01b |
| 030: | 001 | 09d | 0f8 | 1a0 | 16d | 1f3 | 01c | 146 | 07d | 0d1 | 082 | 1ea | 183 | 12d | 0f4 | 19e |
| 040: | 1d3 | 0dd | 1e2 | 128 | 1e0 | 0ec | 059 | 091 | 011 | 12f | 026 | 0dc | 0b0 | 18c | 10f | 1f7 |
| 050: | 0e7 | 16c | 0b6 | 0f9 | 0d8 | 151 | 101 | 14c | 103 | 0b8 | 154 | 12b | 1ae | 017 | 071 | 00c |
| 060: | 047 | 058 | 07f | 1a4 | 134 | 129 | 084 | 15d | 19d | 1b2 | 1a3 | 048 | 07c | 051 | 1ca | 023 |
| 070: | 13d | 1a7 | 165 | 03b | 042 | 0da | 192 | 0ce | 0c1 | 06b | 09f | 1f1 | 12c | 184 | 0fa | 196 |
| 080: | 1e1 | 169 | 17d | 031 | 180 | 10a | 094 | 1da | 186 | 13e | 11c | 060 | 175 | 1cf | 067 | 119 |
| 090: | 065 | 068 | 099 | 150 | 008 | 007 | 17c | 0b7 | 024 | 019 | 0de | 127 | 0db | 0e4 | 1a9 | 052 |
| 0a0: | 109 | 090 | 19c | 1c1 | 028 | 1b3 | 135 | 16a | 176 | 0df | 1e5 | 188 | 0c5 | 16e | 1de | 1b1 |
| 0b0: | 0c3 | 1df | 036 | 0ee | 1ee | 0f0 | 093 | 049 | 09a | 1b6 | 069 | 081 | 125 | 00b | 05e | 0b4 |
| 0c0: | 149 | 1c7 | 174 | 03e | 13b | 1b7 | 08e | 1c6 | 0ae | 010 | 095 | 1ef | 04e | 0f2 | 1fd | 085 |
| 0d0: | 0fd | 0f6 | 0a0 | 16f | 083 | 08a | 156 | 09b | 13c | 107 | 167 | 098 | 1d0 | 1e9 | 003 | 1fe |
| 0e0: | 0bd | 122 | 089 | 0d2 | 18f | 012 | 033 | 06a | 142 | 0ed | 170 | 11b | 0e2 | 14f | 158 | 131 |
| 0f0: | 147 | 05d | 113 | 1 cd | 079 | 161 | 1a5 | 179 | 09e | 1b4 | 0cc | 022 | 132 | 01a | 0e8 | 004 |
| 100: | 187 | 1ed | 197 | 039 | 1bf | 1d7 | 027 | 18b | 0c6 | 09c | 0d0 | 14e | 06c | 034 | 1f2 | 06e |
| 110: | 0ca | 025 | 0ba | 191 | 0fe | 013 | 106 | 02f | 1ad | 172 | 1db | 0c0 | 10b | 1d6 | 0f5 | 1ec |
| 120: | 10d | 076 | 114 | 1ab | 075 | 10c | 1e4 | 159 | 054 | 11f | 04b | 0c4 | 1be | 0f7 | 029 | 0a4 |
| 130: | 00e | 1f0 | 077 | 04d | 17a | 086 | 08b | 0b3 | 171 | 0bf | 10e | 104 | 097 | 15b | 160 | 168 |
| 140: | 0d7 | 0bb | 066 | 1ce | 0fc | 092 | 1c5 | 06f | 016 | 04a | 0a1 | 139 | 0af | 0f1 | 190 | 00a |
| 150: | 1aa | 143 | 17b | 056 | 18d | 166 | 0d4 | 1fb | 14d | 194 | 19a | 087 | 1f8 | 123 | 0a7 | 1b8 |
| 160: | 141 | 03c | 1f9 | 140 | 02a | 155 | 11a | 1a1 | 198 | 0d5 | 126 | 1af | 061 | 12e | 157 | 1dc |
| 170: | 072 | 18a | 0aa | 096 | 115 | 0ef | 045 | 07b | 08d | 145 | 053 | 05f | 178 | 0b2 | 02e | 020 |
| 180: | 1d5 | 03f | 1c9 | 1e7 | 1ac | 044 | 038 | 014 | 0b1 | 16b | 0ab | 0b5 | 05a | 182 | 1c8 | 1d4 |
| 190: | 018 | 177 | 064 | 0cf | 06d | 100 | 199 | 130 | 15a | 005 | 120 | 1bb | 1bd | 0e0 | 04f | 0d6 |
| 1a0: | 13f | 1c4 | 12a | 015 | 006 | 0ff | 19b | 0a6 | 043 | 088 | 050 | 15f | 1e8 | 121 | 073 | 17e |
| 1b0: | 0bc | 0c2 | 0c9 | 173 | 189 | 1f5 | 074 | 1cc | 1e6 | 1a8 | 195 | 01f | 041 | 00d | 1ba | 032 |
| 1c0: | 03d | 1d1 | 080 | 0a8 | 057 | 1b9 | 162 | 148 | 0d9 | 105 | 062 | 07a | 021 | 1ff | 112 | 108 |
| 1d0: | 1c0 | 0a9 | 11d | 1b0 | 1a6 | 0 cd | 0f3 | 05c | 102 | 05b | 1d9 | 144 | 1f6 | 0ad | 0a5 | 03a |
| 1e0: | 1cb | 136 | 17f | 046 | 0e1 | 01e | 1dd | 0e6 | 137 | 1fa | 185 | 08c | 08f | 040 | 1b5 | 0be |
| 1f0: | 078 | 000 | 0ac | 110 | 15e | 124 | 002 | 1bc | 0a2 | 0ea | 070 | 1fc | 116 | 15c | 04c | 1c2 |
La fonction FL
La fonction FL prend deux paramètres. Le premier est une entrée de 32 bits nommée FL_IN, l'autre est un index d'EK noté k. FL renvoie un buffer de 32 bits de données nommé FL_OUT.
fonction FL(FL_IN, k)
variables d0, d1 (entiers de 16 bits)
début
d0 = FL_IN >> 16
d1 = FL_IN & 0xffff
si (k est pair) alors
d1 = d1 ^ (d0 & EK[k/2])
d0 = d0 ^ (d1 | EK[(k/2+6)%8+8])
sinon
d1 = d1 ^ (d0 & EK[((k-1)/2+2)%8+8])
d0 = d0 ^ (d1 | EK[((k-1)/2+4)%8])
finsi
FL_OUT = (d0<<16) | d1
retourner FL_OUT
fin
Quand l'algorithme est utilisé pour le déchiffrement, la fonction FLINV est utilisée à la place de FL.
fonction FLINV (FL_IN, k)
variables d0, d1 (entiers de 16 bits)
début
d0 = FL_IN >> 16
d1 = FL_IN & 0xffff
si (k est pair) alors
d0 = d0 ^ (d1 | EK[(k/2+6)%8+8])
d1 = d1 ^ (d0 & EK[k/2])
sinon
d0 = d0 ^ (d1 | EK[((k-1)/2+4)%8])
d1 = d1 ^ (d0 & EK[((k-1)/2+2)%8+8])
finsi
FL_OUT = (d0<<16) | d1
retourner FL_OUT
fin
Description du chiffrement/déchiffrement
On utilise en général un chiffrement/déchiffrement en 8 tours. Un tour consiste en un appel à la fonction FO, les tours paires incluent en plus un appel à FL ou FLINV. Après le tour final un appel à FL ou FLINV est effectué.
Voici les descriptions détaillées des tours pour le chiffrement :
Un texte clair P de 64 bits est divisé en D0 (les 32 bits de poids fort) et D1 (les 32 bits de poids faible).
début
// tour 0
D0 = FL(D0, 0);
D1 = FL(D1, 1);
D1 = D1 ^ FO(D0, 0);
// tour 1
D0 = D0 ^ FO(D1, 1);
// tour 2
D0 = FL(D0, 2);
D1 = FL(D1, 3);
D1 = D1 ^ FO(D0, 2);
// tour 3
D0 = D0 ^ FO(D1, 3);
// tour 4
D0 = FL(D0, 4);
D1 = FL(D1, 5);
D1 = D1 ^ FO(D0, 4);
// tour 5
D0 = D0 ^ FO(D1, 5);
// tour 6
D0 = FL(D0, 6);
D1 = FL(D1, 7);
D1 = D1 ^ FO(D0, 6);
// tour 7
D0 = D0 ^ FO(D1, 7);
// final
D0 = FL(D0, 8);
D1 = FL(D1, 9);
fin
Le texte chiffré C de 64 bits est construit à partir de D0 et D1 de la manière suivante :
C = (D1<<32) | D0;
Lors du déchiffrement, l'ordre des tours est inversé :
début
D0 = C & 0xffffffff;
D1 = C >> 32;
D0 = FLINV(D0, 8);
D1 = FLINV(D1, 9);
D0 = D0 ^ FO(D1, 7);
D1 = D1 ^ FO(D0, 6);
D0 = FLINV(D0, 6);
D1 = FLINV(D1, 7);
D0 = D0 ^ FO(D1, 5);
D1 = D1 ^ FO(D0, 4);
D0 = FLINV(D0, 4);
D1 = FLINV(D1, 5);
D0 = D0 ^ FO(D1, 3);
D1 = D1 ^ FO(D0, 2);
D0 = FLINV(D0, 2);
D1 = FLINV(D1, 3);
D0 = D0 ^ FO(D1, 1);
D1 = D1 ^ FO(D0, 0);
D0 = FLINV(D0, 0);
D1 = FLINV(D1, 1);
P = (D0<<32) | D1;
fin
Notes et références
- Bar-On et Keller 2016.
- (en)_[https://web.archive.org/web/20000823133547/http://www.mitsubishi.com/ghp_japan/misty/misty_e_b.pdf_rapport_technique]-2" class="mw-reference-text">Matsui 1997, Publication dans une conférence. Les premières traces sont dans un (en) rapport technique.
Annexes
Liens externes
Bibliographie
- [Bar-On et Keller 2016] (en) Achiya Bar-On et Nathan Keller, « A 2⁷⁰ Attack on the Full Misty1 », Crypto, (DOI 10.1007/978-3-662-53018-4_16, lire en ligne).
- [Matsui 1997] (en) Mitsuru Matsui, « New block encryption algorithm MISTY », Fast Software Encryption (FSE), (DOI 10.1007/BFb0052334).