Matière nucléaire (physique)
La matière nucléaire est un système idéalisé, de dimension infinie, de nucléons en interaction (protons et neutrons), maintenus ensemble par les seules forces nucléaires[1], sans faire intervenir la répulsion électrostatique entre les protons (force de Coulomb). Le volume infini implique qu'il n'y a pas d'effets de surface et que les propriétés de la matière sont invariantes par translation (identiques en tous points).
La détermination des propriétés de la matière nucléaire à partir de l'interaction nucléaire forte, ou plus exactement de l'interaction nucléon-nucléon[2] qui en résulte, est au centre des recherches théoriques de ce domaine. C'est une étape pour dériver les propriétés des noyaux réels et finis à partir d'une force réaliste entre les nucléons et pour étudier des objets cosmologiques comme les étoiles à neutrons (voir Chapitre VIII de la référence[2] - Astrophysique nucléaire).
Objectifs scientifiques
"Malgré son idéalisation, la compréhension des propriétés de la matière nucléaire est une condition préalable à toute théorie cohérente des noyaux, car un morceau fini de matière nucléaire constitue le noyau des noyaux lourds. L'étude de la matière nucléaire complète ainsi les approches portant sur les propriétés spécifiques des noyaux individuels. À son tour, la matière nucléaire ne fournit qu'une description grossière (synthétique) des noyaux, car elle néglige les principaux effets de taille finie"[3].
Les deux caractéristiques principales de la matière nucléaire proche de son état fondamental, sont sa densité et le rapport du nombre des protons au nombre des neutrons.
- La densité nucléaire est traditionnellement exprimée en nombre de nucléons par fermi3 ou comme une masse volumique en kg/m3. La densité de référence est celle du centre des noyaux lourds (environ 0,15 nucléon par fermi3 ) ; elle est directement reliée au terme d'énergie de volume dans les formules de masse du modèle de la goutte liquide du noyau.
- Le rapport du nombre des protons et du nombre des neutrons. Une idéalisation courante est la matière nucléaire symétrique, qui se compose d'un nombre égal de protons et de neutrons. Ce rapport est beaucoup plus petit, lorsque l'on modélise la matière des étoiles à neutrons (voir infra), qui peut inclure en outre, des électrons.
En analogie avec les systèmes thermodynamiques, on peut définir une équation d'état de la matière qui relie son énergie (ou la température) à la densité et/ou à la pression . L'énergie est mesurée en MeV par nucléon, (traditionnellement notée MeV/A ou MeV/u).
En analogie avec la thermodynamique des gaz réels, la matière nucléaire pourra exister sous différentes phases (voir infra). Mais à des énergies et/ou des pressions très élevées, on s'attend, sur la base de la liberté asymptotique de la chromodynamique quantique, à ce qu'elle devienne de la matière de quarks, qui est un gaz de Fermi dégénéré de quarks[4].
Équation d'état nucléaire
Potentiel nucléon-nucléon
L'idéal théorique serait de pouvoir déduire l'équation d'état nucléaire de l'interaction nucléaire forte entre ses composants. Cet idéal est inatteignable, car
- d'une part, si l'interaction nucléon-nucléon libre (dans le vide) est expérimentalement connue, elle ne peut être formellement déduite de la théorie QCD sous-jacente. Des formes paramétrées ont été déduites pour reproduire au mieux les données expérimentales (par exemple, le potentiel de Paris[5]).
- d'autre part, l'interaction entre les nucléons dans la matière nucléaire - en particulier dense et chaude - ne peut se réduire à des interactions de paires ; il faut introduire les effets des nucléons voisins en raison du principe d'exclusion de Pauli. Les calculs théoriques (par exemple la théorie de Goldstone- Brückner)[6] donnent des aperçus sur la structure de la matière nucléaire, mais ne reproduisent que de manière approximative les données expérimentales, comme la densité et l'énergie de liaison de la matière dans son état fondamental[3]. Les modèles plus phénoménologiques utilisent des forces nucléon-nucléon effectives, qui incorporent au mieux les effets du milieu sur l'interaction entre paire de nucléons[7].
Équation d'état phénoménologique
Pour étudier l'équation d'état nucléaire, de nombreuses forces effectives ont été utilisées (pour une revue voir la référence[8]). Parmi les plus populaires, les interactions effective, dites de Skyrme, font l'hypothèse que les interactions sont de contact (portée nulle), ce qui conduit à des expressions simples de l'équation d'état, qui dépend de 3 paramètres , , :
Les paramètres sont ajustés pour retrouver la densité nucléaire et l'énergie de liaison par nucléon de 16 MeV dans l'état fondamental (point de saturation).
Ces modèles permettent de déduire des caractéristiques essentielles de la matière nucléaire autour du point de saturation[3] :
- La compressibilité de la matière nucléaire, caractéristique essentielle dans les collisions d'ions lourds ou les résonances géantes (pour une discussion détaillée voir la référence[9]).
- Une transition de phase de type liquide-gaz (qui correspond à la dissociation des systèmes de nucléons liés en "gaz" de nucléons).
- une zone d'instabilité à basse densité où la matière se dissocie en un ensemble de noyaux légers et de nucléons libres (instabilités spinodales)[10].
Les différentes phases de la matière nucléaire
Loin du point de saturation, la matière n'est plus composée uniquement de nucléons ; de nouvelles phases apparaissent. La figure présente de manière qualitative les différentes phases attendues.
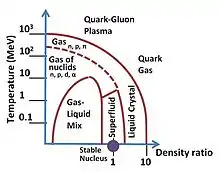
Autour du point de saturation, le principe de Pauli bloque les collisions entre les nucléons ; la matière nucléaire se comporte comme un liquide quantique superfluide. Aux plus faibles densités, on retrouve la zone de coexistence liquide (noyaux légers) - gaz (nucléons), calculable avec les forces effectives (voir supra). Lorsque l'énergie d'excitation (de) augmente, les fragments légers se dissocient en protons, neutrons et particules alpha.
Aux hautes énergies d'excitation, les seuils de création de particules nouvelles, comme les pions, sont franchis et dans des conditions plus extrêmes, la théorie prévoit la dissociation de toutes les particules composites en leurs constituants (plasma de quarks et de gluons).
Les étoiles à neutrons
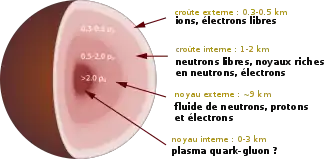
La composition d'une étoile à neutrons, qui nécessite plus que des neutrons et des protons, n'est pas nécessairement neutre de charge localement et ne présente pas d'invariance de translation, est souvent appelée différemment, par exemple, matière d'étoile à neutrons ou matière stellaire et est considérée distincte de la matière nucléaire[11] - [12]. Dans une étoile à neutrons, la pression monte de zéro (à la surface) à une grande valeur inconnue au centre.
Voir également
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Nuclear matter » (voir la liste des auteurs).
- « Essentiel sur 4 interactions fondamentales », sur cea.fr (consulté le )
- Luc Valentin, Le monde subatomique : des quarks aux centrales nucleaires., Hermann, (ISBN 2-7056-6043-7 et 978-2-7056-6043-7, OCLC 300428165, lire en ligne)
- (en) Eric Suraud et Bernard Tamain, Nuclear dynamics in the nucleonic regime, Institute of Physics Pub, (ISBN 0-7503-0537-1 et 978-0-7503-0537-2, OCLC 44493394, lire en ligne)
- (en) Stefan B Rüster, Pairing in fermionic systems, World Scientific, (ISBN 981-256-907-3, lire en ligne), « Phase diagram of neutral quark matter at moderate densities »
- (en) M. Lacombe, B. Loiseau, J. M. Richard et R. Vinh Mau, « Parametrization of the Paris N − N potential », Physical Review C, vol. 21, no 3, , p. 861–873 (ISSN 0556-2813, DOI 10.1103/PhysRevC.21.861, lire en ligne, consulté le )
- (en) B. D. DAY, « Elements of the Brueckner-Goldstone Theory of Nuclear Matter », Reviews of Modern Physics, vol. 39, no 4, , p. 719–744 (DOI 10.1103/RevModPhys.39.719, lire en ligne, consulté le )
- (en) J. Dechargé et D. Gogny, « Hartree-Fock-Bogolyubov calculations with the D 1 effective interaction on spherical nuclei », Physical Review C, vol. 21, no 4, , p. 1568–1593 (ISSN 0556-2813, DOI 10.1103/PhysRevC.21.1568, lire en ligne, consulté le )
- (en) D. Davesne, P. Becker, A. Pastore et J. Navarro, « Infinite matter properties and zero-range limit of non-relativistic finite-range interactions », Annals of Physics, vol. 375, , p. 288–312 (ISSN 0003-4916, DOI 10.1016/j.aop.2016.10.013, lire en ligne, consulté le )
- (en) J. Treiner, H. Krivine, O. Bohigas et J. Martorell, « Nuclear incompressibility: From finite nuclei to nuclear matter », Nuclear Physics A, vol. 371, no 2, , p. 253–287 (ISSN 0375-9474, DOI 10.1016/0375-9474(81)90067-1, lire en ligne, consulté le )
- B. Jacquot, Instabilités spinodales dans les noyaux atomiques, Ganil - Caen, Thèse de l'Université de Caen, (lire en ligne)
- Francesca Gulminelli, Collective Motion and Phase Transitions in Nuclear Systems, World Scientific, (ISBN 981-270-083-8, lire en ligne), « Nuclear matter versus stellar matter »
- Norman K. Glendenning, Compact stars, Springer, (ISBN 0-387-98977-3, lire en ligne), p. 242





