Métapopulation
En écologie, le concept de métapopulation désigne un ensemble de populations d'individus d'une même espèce séparées spatialement ou temporellement, mais interconnectées par la dispersion. Ces populations occupent des parcelles d'habitat de qualité variable et, à tout moment, certaines parcelles peuvent être disponibles et inoccupées. La zone intermédiaire, appelée la matrice de l'habitat, est vue comme inutilisable, mais peut être traversée.
Origine du concept
Ce concept est apparu pour la première fois dans la littérature écologique en 1969. Il fut formulé par le mathématicien Richard Levins à la suite de ses travaux sur un modèle de dynamique de populations d'insectes nuisibles à l'agriculture. Par la suite, de nombreux écologues reprirent et approfondirent ce concept, notamment pour l'étude de populations soumises à la fragmentation écopaysagère, en l'adaptant aussi bien à la vie marine que microbienne, tel l'écologiste finlandais Ilkka Hanski.
Caractérisation d'une métapopulation
Sur son aire de distribution, sauf au tout début de l'apparition d'une espèce nouvelle, chaque métapopulation voit sa distribution discontinuer par cause de fragmentation géographique ou écopaysagère.
L'importance spatiale de l'aire étudiée et la durée de l'étude ont une grande importance pour l'étude des métapopulations[1], tout particulièrement pour des espèces à longue durée de vie et à faible taux de reproduction.
Importance des métapopulations
La persistance d'une population dépend : des interactions spécifiques, des caractéristiques écopaysagères (dont hétérogénéité spatiale et connectivité, notamment via des écotones, ou au contraire fragmentation écologique), des phénomènes de stochasticité démographique et environnementale ou encore des problèmes de types écotoxicologique. L'étude de ces différents facteurs de viabilité relève notamment de la biologie de la conservation et de l'évaluation environnementale.
Au sein d'une métapopulation, la population d'un patch d'habitat peut s’éteindre. Ce dernier peut ensuite être recolonisé à la suite de la dispersion d'individus d’autres patchs. La métapopulation dans son ensemble peut alors être stable, même si certaines parties fluctuent. Sa persistance dépend donc d'un équilibre stochastique entre les extinctions locales et la recolonisation de patchs vacants. Cependant, l'isolement et l'éloignement progressif des habitats peuvent entrainer l'extinction de populations et de la métapopulation.
Aujourd'hui, de nouvelles méthodes de gestion du vivant ont vu le jour afin de prendre en compte la dynamique des métapopulations dans la conservation des espèces (corridors écologiques, réserves naturelles, écoducs…).
Historique du concept
Les premières expériences sur les interactions proies-prédateurs et l'hétérogénéité spatiale menées par Gause (1930), puis par Huffaker (1958) ont permis l’émergence du concept de métapopulation.
Gause avait dans un premier temps constaté que les populations de prédateurs et de proies étaient vouées à s'éteindre indépendamment de leur taille initiale. Il n'avait alors pas vérifié les équations de Lotka-Volterra, qui prédisaient des oscillations de populations de proie-prédateur au fil du temps. Cependant en introduisant des refuges pour la population de proies et l'immigration dans le modèle, les cycles de population représentaient avec précision ces oscillations.
L’expérience de Huffaker sur les interactions proies-prédateurs, 1958
Les expériences de Huffaker ont ensuite élargi celles de Gause en examinant la façon dont la dispersion et l'hétérogénéité spatiale pouvaient conduire à des oscillations prédateur-proie.
Il a ainsi tenté de démontrer que les refuges n'étaient pas nécessaires au maintien de populations de proies. Il pensait plutôt que l'hétérogénéité spatiale et ses différents effets sur la capacité de dispersion de l'espèce étaient ce qui permettait de créer un refuge par le déplacement de la population de proies. En effet, en créant un système inégal facilitant la dispersion de proies par rapport à celle de leurs prédateurs, Huffaker est parvenu à un système de dynamique prédateur-proie à trois cycles de fluctuation de la population.
Même si le terme métapopulation n’avait pas encore été inventé, les facteurs environnementaux (hétérogénéité spatiale et microrépartition de l'habitat) décriront plus tard les conditions d'une métapopulation relative à la façon dont les groupes de populations spatialement séparés interagissent les uns avec les autres.
On sait aujourd'hui que la dynamique des systèmes proie-prédateur dans les métapopulations est influencée par les relations spatiales et les modes d’organisation des mouvements. À l’échelle du patch de proie individuelle d’une métapopulation, la rencontre des proies avec un prédateur signifie le plus souvent l'extinction locale de cette population. À l’échelle régionale cependant, les systèmes proies-prédateurs persistent car les modes d’organisation de la dispersion des 2 espèces dans une hétérogénéité d’habitats créent une mosaïque d’extinctions et de recolonisation entre les patchs d’habitat (McLaughlin & Roughgarden, 1993).
Théorie de la biogéographie insulaire : MacArthur et Wilson, 1967
La théorie de la biogéographie insulaire a été proposée par Robert MacArthur et Edward Osborne Wilson en 1967.
Si la richesse spécifique d’une île est, à surface et région équivalente, toujours inférieure à celle d’un continent, les dynamiques des populations insulaires restaient encore largement méconnues des écologues. Cette théorie a par la suite été étendue aux écosystèmes continentaux complexes où l’on peut associer des îlots à des parcelles d’habitats isolées.
MacArthur et Wilson décrivirent un système de dynamique résultant du taux de migration d’individus continentaux et du taux d'extinction des espèces, et où les paramètres influençant les richesses spécifiques insulaires étaient la surface des îles et l’éloignement au continent.
En effet, ils avaient constaté que si le taux d’immigration était trop faible, une dynamique locale insulaire ne pouvait être stable à cause d’évènements stochastiques risquant d’entraîner l’extinction de la population (mortalités inhérentes à l'environnement, la prédation, les interactions compétitives)[2].
Afin d’illustrer leurs théories d’exemples empiriques, ils ont alors comparé leur modèle prédictif avec l’évolution de la richesse spécifique du Krakatoa. L’explosion du volcan en 1883 avait détruit toute forme de vie sur l’île. Le suivi de la recolonisation de l’île leur a permis d’observer une forte concordance des résultats avec leur théorie.
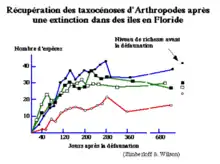
L'un des meilleurs exemples illustrant la théorie de MacArthur et Wilson est une étude menée en Floride vers la fin des années 1960 par Simberloff et Wilson. Ils ont réalisé un inventaire complet des arthropodes vivant sur quelques îlots de mangroves et les ont ensuite exterminés par fumigation. Cette étude a permis de développer le concept de nombre d’espèce à l’équilibre et de vérifier l’influence de la taille des îles et de leur distance par rapport à l’écosystème source sur leur colonisation.
Les résultats de cette étude montrent que la recolonisation est très rapide car après 200 jours, le nombre d'espèces des 4 îles se stabilise à des valeurs semblables à celles relevées avant la défaunation. Ce rééquilibrage final est dû au réajustement de la niche écologique des espèces par la mise en jeu d’interactions interspécifiques.
Naissance du terme : Richard Levins, 1969
Le fondement du concept de métapopulation revient à Richard Levins en 1969, qui compare la métapopulation à un ensemble de populations locales instables habitant des parcelles d'habitat discrètes. Selon ses propres mots, il s'agit d '«une population de populations ».
Modélisation
Différentes approches permettent de caractériser les métapopulations :
- L'approche classique que l'on dit spatialement implicite : où les individus ont la même probabilité d'aller dans un patch d'habitat que dans un autre. Le modèle de Levins est spatialement implicite.
- L'approche spatialement explicite : dans laquelle ce sont cette fois les patchs d'habitats les plus proches qui sont le plus susceptibles d'échanger des individus.
Ces modèles sont directement applicables pour la gestion car ils prennent en compte le fait que la diminution d'une métapopulation est d’autant plus rapide que la dispersion est limitée dans l’espace.
Il existe enfin des modèles où il y a une variation continue de l'habitat, sans patchs et qui servent à étudier la façon dont ces patchs émergent en réponse à la dispersion.
Les différents types de métapopulations
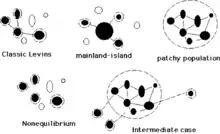
Modèle classique de la métapopulation, R. Levins
C’est un vaste réseau de petites parcelles similaires (occupées en noir ou inoccupées en blanc), avec des dynamiques locales qui se produisent à une échelle de temps beaucoup plus rapide que la dynamique de la métapopulation entière. Ce modèle est parfois utilisé pour décrire un système dans lequel toutes les populations locales ont un risque élevé d'extinction. Il est aussi appelé patch occupancy model.
Modèle ile-continent « MacArthur et Wilson »
Comme vu précédemment ce modèle caractérise un ensemble de parcelles d'habitat situées à distance d'une très grande parcelle d'habitat où la population locale ne va jamais s'éteindre et qui sert de source aux plus petites.
Source-puits « Pulliam »
Le modèle source-puits de dynamique des métapopulations prend en compte les différences dans la qualité des parcelles d'habitat : Dans les parcelles sources, où les ressources sont abondantes : les individus produisent plus de descendants que nécessaire pour les remplacer (croissance positive de la population). Le surplus de progéniture est dispersé vers d'autres parcelles (exportations nettes). Dans les parcelles puits, où les ressources sont rares : les populations sont maintenues par l’immigration d'individus (importateurs nets) et les taux de croissance sont négatifs sans immigration.
Le modèle de dynamique source-puits développé par Pulliam est appelé modèle “BIDE rates”. Il soutient que l'équilibre de chaque patch sera atteint si :
B (naissance) + I (immigration) – D (mort) – E (émigration) = 0
Soit pour la métapopulation lorsque la somme est égale à 0. Il définit donc à l'équilibre qu’un patch sera source si b>d et e>i et qu’un autre sera puits si d>b et i>e. Pulliam considère dans ce modèle la variabilité de l'habitat.
Métapopulation de non équilibre
C’est un système dans lequel les taux d'extinction à long terme dépassent la colonisation ou vice-versa. Un cas extrême est celui où l'isolement des populations est si grand que la dispersion (et donc recolonisation) est exclue.
Cas intermédiaire
Un cas intermédiaire constitue un mélange des modèles île-continent, source-puits et de non équilibre.
Modélisation de l’approche classique spatialement implicite de Levins
Levins suppose que tous les habitats potentiels d'une métapopulation ne sont jamais tous occupés. Il y a toujours des patchs inoccupés qui seront recolonisés ainsi que des patchs occupés où les populations vont disparaître. La différence avec le modèle de l'équilibre dynamique de Mac Arthur et Wilson est que la colonisation ne se fait plus de manière constante à partir d'une source continue, mais à partir de plusieurs patchs déjà occupés.
Son modèle est fondé sur 4 hypothèses :
- L’habitat convenable est fait de patchs identiques distincts où la population locale produit des dispersants.
- Toutes les populations locales ont le même risque d'extinction. Si ce cas n'est pas vérifié, la persistance de la métapopulation dépendrait simplement de la persistance de la plus grande population et la métapopulation considérée serait de type continent-île.
- L'isolement des patchs ne peut pas empêcher leur recolonisation, sans laquelle la métapopulation serait dans un état de non-équilibre et en danger d'extinction. L'espace est implicite dans ce modèle, il n'existe pas de structuration spatiale des patchs et les individus ont une probabilité identique de disperser dans chacun d'eux.
- Les dynamiques des populations locales ne sont pas totalement synchrones. Autrement, la persistance de la métapopulation dépendrait uniquement de la persistance de la population au plus petit risque d'extinction.
Le nombre d’habitats occupés par l'espèce au sein de la métapopulation (P) est donné par la résolution de l'équation différentielle :
dP/dT= cP (1-P) - eP
La colonisation s'exprime par le produit de la probabilité de coloniser un patch inoccupé (c) et du nombre de sites inoccupés (1-p) pondéré par le nombre de sites occupés (p).
L'extinction s'exprime par le produit de la probabilité qu'un patch occupé devienne disponible (e) et du nombre de sites occupés (p).
Les équilibres de l’équation :
Lorsque dP/dT = 0, le taux de gain de nouveaux habitats est égal au taux de perte : cp(1-p) – ep = 0 D’où : P*=0 (équilibre trivial) ou P*=1-(e/c) (équilibre stable)
Donc selon le modèle de Levins, le nombre de sites occupés à l’équilibre (p*) est positif si le taux d’extinction est inférieur au taux de colonisation (c>e).
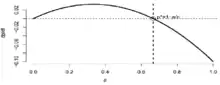
Taux de changement de la proportion d’habitat occupé avec p* l’optimum de taux de changement
Des prédictions sont apportées à ce modèle : la proportion de parcelles occupées augmente avec la surface des parcelles puisque le taux d’extinction diminue à mesure que la taille des parcelles augmente mais elle augmente aussi à mesure que la distance entre les parcelles se réduit puisque le taux de colonisation augmente.
Addition de réalisme dans le modèle de Levins
Plusieurs hypothèses permettent l'ajout de réalisme dans le modèle de Levins :
- Lier la migration et les extinctions locales
- Comptabilisation de la destruction des habitats (c'est-à-dire, le nombre réel de patchs disponibles pour la recolonisation)
Hypothèse 1 : la colonisation (c) et l'extinction (e) sont supposés indépendants par Levins, mais ces deux paramètres sont probablement liés :
- les corridors peuvent apporter des immigrants, ce qui permettrait l'augmentation de (c), mais peuvent aussi apporter des agents pathogènes, prédateurs, etc., ce qui augmenteraient l’extinction (e).
- la modélisation de cet ajustement montre que l'extinction de la métapopulation augmente si les effets négatifs de la connectivité contrebalancent les effets positifs (Hess GR, 1996).
La nouvelle équation serait alors :
dP/dt = r(c) p (1-p) - x(c)P et : p* = 1 - x(c)/r(c)
ec :
r(c) = le taux de recolonisation comme fonction de la connectivité x(c) = le taux d’extinction locale comme fonction de la connectivité
Maintenant r(c) doit être supérieur à x(c) pour que l’on ait un équilibre non nul (une métapopulation non en voie d’extinction).
Hypothèse 2 : le modèle simple suppose qu’une parcelle est immédiatement disponible pour la recolonisation après l’extinction d’une population locale, mais souvent l’extinction se produit parce que l'habitat est détruit et la recolonisation ne peut pas se produire jusqu'à ce que cette parcelle régénère. La proportion des parcelles disponibles pour la recolonisation n’est donc pas (1-P) mais (H-P), où (H) est la fraction du nombre de parcelles totales qui est régénérée. L'extinction locale est maintenant fonction d’événements stochastiques (démographiques et environnementaux) et de la destruction des parcelles.
On a alors : ^P = H - (e+d) / c (où d est le taux d’extinction en raison de la destruction des parcelles)
Connectivité et graphique de persistance d'une métapopulation
La survie d’une métapopulation dépend particulièrement de leur « seuil de persistance » liée à des paramètres comme la connectivité. La présence et la nature des cycles de cette métapopulation peut être représente par un graphe grâce à la théorie des graphes qui est ici pertinente.
Modèle de base
La métapopulation est constituée de n populations, contenant des individus d’une même espèce regroupés en m classes d’âge. Le vecteur représentant la population i est noté Ni (t) à la date t, et le j-ième coefficient de Ni (t) est le nombre d’individus appartenant à la j-ième classe d’âge à la date t. La métapopulation est représentée par la matrice m . n notée N(t), où la i-ième colonne représente la population i. La matrice de Leslie associée au système est L, telle que : N(t+1) = L.N(t). On note pk, la probabilité de survie d’un individu d’âge k-1 jusqu’à l’âge k. fk est le taux de fécondité de la classe k, alors que _ est la proportion de jeunes de la population qui est « auto-recrutée » avec succès après la phase de dispersion. On peut noter alors :
Cette matrice peut être vue comme la combinaison linéaire d’une matrice « de survie » P et d’une matrice « de fécondité » F : L = P + σF avec:
Les matrices P et F peuvent être distinctes selon chaque population, et seront alors notées Pi et Fi. On note R, le "nombre de reproduction", représentant le nombre moyen de jeunes produits durant la vie d’un individu, défini par :
À partir de ces outils de base, on peut étudier les conditions de la persistance de la métapopulation.
Le modèle de n populations connectés
On créant une métapopulation, représentée par un graphe G dont les sommets sont les n populations, et les arêtes sont les flux de larves. Quelques hypothèses de travail sont proposées :
- les matrices de fertilité et de survie sont identiques pour toutes les populations ;
- la matrice de connectivité C est définie par Ci;j = proportion de jeunes produits en j qui sont recrutés avec succès par la population i ;
- sans hypothèse supplémentaire, χ = λC .R, où λC est le rayon spectral de C (soit sa plus grande valeur propre) ;
- les auteurs font l’hypothèse que le nombre de jeunes qui immigrent dans une population j est en moyenne une proportion α de leur population d’origine j.
On peut alors considérer G comme un graphe non-orienté non pondéré ; sa matrice d’adjacence A (aij = 1 s’il existe une voie de dispersion directe entre i et j, aii = 0 8 i) est donc symétrique réelle. En particulier, la matrice de connectivité s’écrit sous la forme : C = σI + αλA, où I est la matrice identité, et λA le rayon spectral de A. Dans ces conditions, le paramètre de persistance s’écrit : χ=(σ+αλA).R
On peut en tirer quelques conclusions immédiates et plutôt intuitives : si toutes les populations sont des « puits » (id est, ne peuvent pas se renouveler sans apport de larves extérieures : σR < 1), c’est la structure du réseau qui détermine la survie de la métapopulation, via le rayon spectral A. Une dispersion importante et efficace se traduit par un paramètre α élevé, et aide au maintien des effectifs.
On peut réaliser une étude de l’influence de la structure du réseau sur la persistance de la métapopulation.
Influence de la topologie du réseau
La répartition des liens est réalisée selon trois modalités principales : G peut être un graphe régulier, ou un graphe aléatoire homogène ou hétérogène.
Graphe régulier
Pour une topologie régulière, tous les sommets ont le même degré k (par exemple : n = 8, k = 2 pour un C8, Le rayon spectral vaut alors k, et on a χ= (σ + αk):R. Les auteurs envisagent le cas où α= σ : alors, l’autorecrutement devient faible devant l’importance de l’immigration, et le degré des sommets contrôle principalement la persistance de la métapopulation.
Graphe aléatoire
Les auteurs utilisent un modèle de graphes aléatoires dû à Erdos et Rényi. Dans ce modèle, il y a une probabilité p pour que deux sommets donnés soient reliés par une arête, ce qu’illustre la figure 2b. On obtient aisément le degré moyen des sommets : k = n:p. De plus, le rayon spectral de A est égal au degré moyen, d’où : χ = (σ + αk)R
Graphe hétérogène
On peut étendre ces résultats à tout graphe aléatoire, en quantifiant leur hétérogénéité. Pour ce faire, on peut utiliser la variable aléatoire k, dont les réalisations ki correspondent au degré de chaque sommet. Le carré du coefficient de variation de k, noté CV 2 et défini par CV 2 = V ar(ki)=k2, est choisi pour représenter l’hétérogénéité du réseau. Par exemple, le réseau présenté en figure 2c est fortement hétérogène (un sommet très connecté, et la plupart des autres non).

Le choix de cette mesure donne l’expression du paramètre de persistance : χ = [σ + αk(1 + CV 2)R]
Qualitativement, on peut interpréter cette formule de la façon suivante : la plus forte valeur propre de A dépend directement du degré du sommet le plus connecté, dmax. On peut s’attendre à ce que dmax soit de l’ordre de la moyenne + la variance divisée par la moyenne, soit k + V ar(ki)=k .χ
Plus G est hétérogène, plus la persistance est forte. Ce résultat, plutôt contre-intuitif, pourrait s’interpréter par la présence de quelques populations à fort nombre reproductif, et fort degré, dont les émigrants suffisent à maintenir toutes les populations qui leur sont connectées.
De plus l’intérêt de la dispersion est conditionné par l’existence de cycles.
Synthèse : cohérence de la population
Si une seule population est capable de s'accroître, alors toutes celles qui lui sont connectées, directement ou non, seront capables de survivre aussi. Plus le réseau de dispersion est fragmenté en sous-réseaux indépendants, moins cette propriété sera exploitée : les auteurs introduisent alors la notion de « cohérence » de la métapopulation. La cohérence recouvre la connexion à grande échelle des sous-réseaux. Elle permet par exemple d’amortir les effets des perturbations extérieures (notion de résilience en écologie), favorise la recolonisation des sites impactés... Une forte cohérence correspond donc à une mutualisation des risques sur l’ensemble de la métapopulation. Toutefois, si les évolutions temporelles des populations sont trop fortement corrélées, le risque d’extinction totale augmente. Une valeur critique de p, la probabilité qu’il existe une arête entre i et j, est souvent retenue pour l’émergence d’un composant cyclique d’une taille de l’ordre de n : p = 1/n.
Il était possible de trouver un paramètre pertinent, permettant d’évaluer correctement la survie d’une métapopulation. La définition de ce paramètre varie selon les cas : le nombre de populations, le degré moyen des sommets de G, la topologie du graphe, son hétérogénéité...
Ce travail montre la puissance de la modélisation et des mathématiques, mais aussi ses limites :
- si l’on veut appliquer ce modèle à une métapopulation réelle, il peut être délicat voire impossible d’évaluer certains paramètres de la modélisation ;
- le modèle repose nécessairement sur des hypothèses simplificatrices (le taux de dispersion est identique pour toute paire de populations connectées), et néglige les interactions inter-spécifiques ainsi que la capacité du milieu ;
- la persistance, si elle est un premier objectif, est souvent conditionnée par la survie d’un maximum de populations, pour des raisons de diversité génétique ; c’est alors la « cohérence du réseau » qui intervient. Cette cohérence est plus difficile à quantifier, bien que la taille du composant cyclique maximal en soit un indicateur intéressant.
La science est capable d’empêcher l’effondrement de certains écosystèmes et la disparition de certaines espèces (bien qu’il soit trop tard pour beaucoup d’entre elles), problèmes très actuels et cruciaux pour la qualité de vie (voire la survie) de centaines de millions de personnes. Mais il est du devoir des scientifiques de rappeler à tous que la plupart de ces problèmes sont reliés directement aux activités humaines, et à une foi excessive en la technologie que la science elle-même a trop longtemps portée.
Implication dans la gestion de l'environnement
Gestion et conservation
La gestion de la biodiversité est la discipline qui regroupe les différentes méthodes utilisées pour la sauvegarde de la diversité biologique. Il existe trois grandes approches : protection, conservation, et restauration.
C’est devenu, depuis quelques années, une préoccupation mondiale, à cause du nombre accru des extinctions d’espèces.
La conservation en biologie, qui étudie principalement les espèces rares, est très concernée par les fragmentations d’habitats et les populations isolées. La conservation peut être in-situ ou ex-situ, la première étant la plus idéale mais pas toujours possible. Dans les deux cas il convient de suivre les espèces à l’aide de modèles écologiques par exemple. La conservation dépend des caractéristiques sociales, économiques et des conditions écologiques de la région.
La métapopulation pour la gestion : intérêt majeur actuel
Le concept de metapopulation est important parce que les espèces qui forment des méta-population font face à des problèmes particuliers liés à l’impact environnemental et a des options de conservation qui peuvent être évaluées plus complètement, ou seulement, dans un contexte de metapopulation.
À ce jour, les nombreuses activités anthropiques ne laissent pas sans conséquence les habitats d’espèces. En effet, les constructions de routes, les déforestations, les ponts reliant une île à un continent, etc. sont à l’origine de fragmentation ou jointure entre différents milieux et populations résidentes. Ceci entraine une perturbation des dispersions d’individus. D’autres évènements, comme des introductions d’espèces volontaires ou non, perturbent les écosystèmes existants ; ceci peut aussi être causé par des activités non anthropiques comme les changements climatiques actuels qui sont à l’origine d’extinctions d’espèces mais aussi de déplacements de niches écologiques ), et de perturbation de cycles saisonniers.
Les modèles en métapopulation permettent de répondre à certaines questions comme : les désavantages de corridors, les bénéfices des populations puits, l’optimal pour la réintroduction, l’avantage entre la réduction d’extinctions contre l’augmentation des colonisations.
Les options de conservation pour les espèces qui existent dans les métapopulations incluent ceux qui visent à augmenter la taille ou la persistance de différentes populations, aussi bien que ceux qui visent à bénéficier le métapopulation. Ainsi, grâce aux modèles vus précédemment, on peut influer sur les différents paramètres connus pour arriver à de bons résultats de gestion. Ainsi, par exemple, en conservation la mise en place de corridors écologiques peuvent apporter des immigrants, ce qui permettrait l'augmentation de la probabilité de colonisation (c) dans le modèle plus réaliste de Levins et la persistance des métapopulations bien qu'on ait des risques d'apporter aussi des agents pathogènes, prédateurs, etc., ce qui augmenteraient l’extinction (e).
Quels sont les avantages du modèle de métapopulation ?
L’étude d’une population peut être faite à l’aide de modèles de métapopulation. En effet, une population est dynamique et sa dynamique dépend aussi des populations avoisinantes. La métapopulation considère une population en tant que dynamique avec l’étude des dispersions. L’approche par la métapopulation permet d’évaluer la persistance des populations dans un état naturel, ou bien à la suite d'une perte ou gain d'habitat, une fragmentation, ainsi que des problèmes générés à la suite d'impacts environnementaux que rencontrent les populations… La métapopulation inclut les processus de formation de patch, de division, les évènements de fusionnement d’habitats, et les troubles. Dans de nombreuses études ces modèles sont grandement utilisés dans un premier temps pour suivre l’évolution de la population, et dans un second temps envisager une intervention là où ce sera le plus efficace pour son maintien.
Cas d’applications
Voici quelques exemples de ce que les modèles de métapopulations nous permettent de faire en ce qui concerne la gestion. À travers ces exemples, nous verrons en quoi les métapopulations nous aident lors de la prise de décision pour la gestion.
La conception de réserves en conservation
La conception de réserves en conservation est un exemple de ce que les modèles de métapopulations nous permettent de réaliser.
À travers ces modèles, le but va être de maximiser la chance de survies des espèces. Cet objectif est atteint par la prédiction et l’observation des plus hauts taux d’extinction généralement dans les plus petites populations, et les plus faibles probabilités de sauvetage par des immigrations dans des patchs plus isolés.
Ainsi, les connaissances dynamique des métapopulations permettent d’orienter nos choix. Par exemple, savoir que plusieurs petites populations peuvent présenter un risque d'extinction inférieur à une large population si le taux de dispersion est suffisamment élevée et le degré de corrélation spatiale du milieu est suffisamment faible, peut orienter la prise de décision. Il faut noter que les petites populations, comparées aux plus grandes, sont elles aussi vulnérables, et par exemple le seront d’autant plus à la stochasticité démographique, une plus haute mortalité de dispersant et l'effet bordure.
Autres cas d’applications pour la gestion
Les modèles de métapopulation permettent d’aider à choisir le type l’intervention pour une conservation optimale des espèces étudiées. Par exemple en ensemençant des graines, ce qui a été le cas pour Zostera marina à la suite d'un épisode catastrophique qui a causé de nombreuses pertes. Ainsi, l’effectif de la population a pu être rapidement restauré.
Les modèles de métapopulations sont aussi intéressants pour prédire des changements liés aux variations climatiques. Ainsi, l’utilisation de ces modèles a permis de faire des prédictions sur les effets des changements sur les papillons. Les papillons sont un cas d’études fréquents en dynamique des métapopulations car ils font les frais de l’activité humaine. Que ce soit à travers l’agriculture intensive qui dégrade les habitats naturels des papillons, ou l’urbanisation qui fragmente leur habitat, ou encore les changements climatiques liés aux activités anthropiques comme le réchauffement climatique ; les papillons voient leur nombre d’espèces diminuer catastrophiquement. D’où la nécessité de ces études de métapopulation pour la conservation. De la même manière, les amphibiens sont aussi très étudiés car eux aussi font les frais de l’activité humaine. Le déclin des populations d'amphibiens fait de ces espèces des espèces menacées d’extinction.
Un autre exemple est la relation proie-prédateur entre un charançon et une plante en voie d’extinction (Aciphylla dieffenbachii). Ce système est un exemple d'une métapopulation consommateur-ressource avec une extinction locale déterministe en raison de la surexploitation des patchs de ressources locales, et montre comment on peut préserver cette espèce. Notamment en maintenant ou améliorant l’hétérogénéité spatiale du système en augmentant par exemple le nombre et la taille des patches.
Limites de l’utilisation des modèles de dynamique des métapopulations
Une limite des modèles de métapopulations en gestion implique le fait qu’on se focalise sur une seule espèce, alors que bien souvent la gestion de la conservation notamment se concentre sur des communautés. Ainsi, les taux de survie et de fécondité dépendent souvent de la compétition à l’intérieur d’un niveau trophique et/ou de la prédation à travers des niveaux trophiques supérieurs.
D’autres limites, liées aux conditions d’expérimentation cette fois ci, peuvent être citées. Notamment pour les prédictions, l’échelle de temps sur laquelle on va récolter les données va être un désavantage lors de prédictions. Ainsi, dans le cas d’une réintroduction d’une espèce menacée qu’est la cicindèle (Cicindela ohlone), le temps de collection des données relatives à la population n’étant pas assez grand, on ne peut pas prévoir avec certitude si la population va fluctuer ou non.
Ces problèmes de prédictions sont intrinsèquement liés aux problèmes de stochasticités environnementales et démographiques.
Échelle de temps, mais aussi échelle spatiale qui, si elle est trop grossière, tend à décrire de façon moins précise les métapopulations. Elles peuvent masquer, par exemple, des microrefuges dans l’habitat où le climat peut être stable qui agit en contre force d’une possible stochasticité environnementale due au climat.
Notes et références
- Burke, V. J., J. L. Greene et J. W. Gibbons. 1995. The effect of sample size and study duration on metapopulation estimates for Slider Turtles (Trachemys scripta). Herpetologica 51(4): 451-456
- Jan-Bernard Bouzillé, Gestion des habitats naturels et biodiversité, Lavoisier, (lire en ligne), p. 129.
Voir aussi
Bibliographie
- (en) Drechsler, Martin Predicting metapopulation lifetime from macroscopic network properties ; Mathematical Biosciences, volume 218, Issue 1, , pages 59-71 (Résumé);
- (en) Hanski, I. Metapopulation Ecology Oxford University Press. 1999. (ISBN 0-19-854065-5)
- (en) Huffaker, C.B. 1958. Experimental Studies on Predation: Dispersion factors and predator-prey oscillations. Hilgardia. 27: 343, p. 83
- (en) Fahrig, L. 2003. Effects of Habitat Fragmentation on Biodiversity. Annual Review of ecology, evolution, and systematics. 34:1, p. 487.
- (en) Janssen, A. et. al. 1997. Metapopulation Dynamics of a Persisting Predator-Prey system.
- (en) Kareiva, p. 1987. Habitat Fragmentation and the Stability of Predator-Prey Interactions. Nature. 326:6111, p. 388.
- (en) Legendre, P. and Fortin, M.J. 1989. Spatial pattern and ecological analysis. Plant Ecology. 80:2, p. 107.
- (en) Levins, R. (1969) "Some demographic and genetic consequences of environmental heterogeneity for biological control." Bulletin of the Entomology Society of America, 71, 237-240
- (en) Levin, S.A. 1974. Dispersion and Population Interactions. The American Naturalist. 108:960, p. 207.
- (en) Real, Leslie A. and Brown, James H. 1991. Foundations of Ecology: Classic papers with commentaries. The University of Chicago Press, Chicago.
- (en) Ronce, Ophélie., Olivieri, Isabelle, Life History Evolution in Metapopulations Ecology, Genetics and Evolution of Metapopulations, 2004, p. 227-257
- (en)Michael C. Whitlock, Selection and Drift in Metapopulations ; Ecology, Genetics and Evolution of Metapopulations, 2004, p. 153-173 (Résumé)
- (en) McLaughlin J. & Roughgarden J. “Species interactions in space.” (1998) Species Diversity in Ecological Communities : Historical and Geographical Perspectives, Ed. by Ricklefs R.E. & Schluter D (chap. 8) : p. 89-98.
- (en) Hanski I., Moilanen A., Pakkala T. & Kuussaari M.“The quantitative incidence function model and persistence of an endangered butterfly metapopulation.” (1996) Conservation Biology (10) : 578-590
- (en) Hess G.R. (1996) American Naturalist (148) : 226-236
- (en) Thomas C. D. and Kunin W. E. “The spatial structure of populations.” (1999) Journal of Animal Ecology (68) : p. 647–657. doi: 10.1046/j.1365-2656.1999.00330.x
- (en) Purcell K.L. & Verner J. “Density and reproductive success of California Towhees.” (1998)Conservation Biology (vol 12, no 2) : p. 442-450
- (en) Hanski I. “Metapopulation dynamics.” (1998) Nature 396 (6706) : 41.
- (en) Edward O.W. Island Biogeography in the 1960s : Theory and Experiment.
- (en) Laura K. Reynolds, Michelle Waycott and Karen J. McGlathery; “Restoration recovers population structure and landscape genetic connectivity in a dispersal-limited ecosystem”;(2013) ]
- (en) Karin Johsta, Katrin Scho¨psb “Persistence and conservation of a consumer–resource metapopulation with local overexploitation of resources” (2003)
- (en) Viktoriia Radchuk, Karin Johst, Jürgen Groeneveldb, Volker Grimmb, Nicolas Schtickzellea; “Behind the scenes of population viability modeling Predicting butterfly metapopulation under climate change”;(2013); Ecological modelling
- (en) Karin Johsta, Katrin Scho¨psb “Persistence and conservation of a consumer–resource metapopulation with local overexploitation of resources” (2003)
- (en) Tara M. Cornelisse*, Michelle K. Bennett, Deborah K. Letourneau; “The Implications of Habitat Management on the Population Viability of the Endangered Ohlone Tiger Beetle (Cicindela ohlone) Metapopulation”; (2013);PLOS one
- (en) Nerissa A. Haby, Thomas A. A. Prowse, Stephen D. Gregory, Michael J. Watts, Steven Delean, Damien A. Fordham, Jeff Foulkes et Barry W. Brook;“Scale dependency of metapopulation models used to predict climate change impacts on small mammals”;(2013)Ecography 36: 832–841
- (en) Resit Akcakaya H., Gus Mills et C. Patrick Doncaster (2006) The role of metapopulations in conservation Topics in Conservation Biology : 64-84
Articles connexes
Liens externes
- Serge Planes, Évolution de la dispersion en milieu fragmenté. CNRS. Lire le document
- Le Groupe de recherche en métapopulations de l'université d'Helsinki.
- (en) Metapopulation models


