Lois de paroi

La première description analytique de la région proche de la paroi dans une couche limite est due à Theodore von Kármán pour l'étude de l'écoulement incompressible sur une plaque plane en 1930[1].

Celle-ci sera modifiée par Ivan Nikuradzé pour prendre en compte l'effet de rugosités pariétales, à partir de nombreux essais utilisant un dépôt de grains de sable calibrés en 1933 et les années suivantes[2]. Ce type de modèle a fait l'objet de multiples lois en utilisant la notion de grain de sable équivalent, chacune étant adaptée à un problème particulier.

Dans les années 1990 une approche par décomposition de domaine a permis de traiter des surfaces comportant des rugosités périodiques et des problèmes analogues comme les parois poreuses et l'injection pariétale de gaz.

Loi linéaire et loi logarithmique comparées au profil réel.

La loi logarithmique a été obtenue par von Kármán en supposant un écoulement sur plaque plane incompressible parallèle à la paroi où les fluctuations liées à la turbulence sont auto-semblables, ne différant d'un point à un autre que par des facteurs d'échelle en espace et en temps. La variable choisie pour exprimer cette hypothèse est la vitesse de frottement qui mesure la fluctuation turbulente. On obtient ainsi[3] - [4]

${\displaystyle u^{+}={\frac {1}{\kappa }}\ln \,y^{+}+C^{+}}$

où

${\displaystyle y^{+}={\frac {y\,u_{\tau }}{\nu }}}$	distance à la paroi normalisée par la vitesse de frottement ${\displaystyle u_{\tau }}$ et la viscosité cinématique ${\displaystyle \nu }$
${\displaystyle u_{\tau }={\sqrt {\frac {\tau _{w}}{\rho }}}\approx {\sqrt {\left|{\overline {u'v'}}\right|}}}$	vitesse de frottement, fonction des fluctuations de vitesse ${\displaystyle u'}$ et ${\displaystyle v'}$
${\displaystyle u^{+}={\frac {u}{u_{\tau }}}}$	vitesse parallèle à la paroi normalisée par ${\displaystyle u_{\tau }}$
${\displaystyle \tau _{w}=\rho \nu {\frac {\mathrm {d} u}{\mathrm {d} y}}}$	cisaillement
${\displaystyle \rho }$	masse volumique
${\displaystyle \kappa }$	constante de von Kármán
${\displaystyle C^{+}}$	constante

L'expérience donne ${\displaystyle \kappa \approx 0.41}$ et ${\displaystyle C^{+}\approx 5.0}$

Le profil de couche limite est donc constitué :

• d'une zone ${\displaystyle \;0<y^{+}\leq 5\;}$ de taille voisine de la dimension de Kolmogorov où la viscosité domine (sous-couche laminaire) et où ${\displaystyle u^{+}\approx y^{+}}$, équation qui résulte de la linéarisation de la relation de définition du cisaillement ;
• d'une région ${\displaystyle \;y^{+}\geq 40\;}$ de turbulence développée caractérisée par la loi logarithmique et dont le sommet est assez mal défini : ${\displaystyle y\gtrsim 0.2\,\delta }$, ${\displaystyle \delta }$ étant l'épaisseur de couche limite. Ce sommet définit une « échelle intégrale » de la couche limite ;
• d'une région externe intermittente caractérisée par une « loi de sillage » ${\displaystyle f\left({\frac {y}{\delta }}\right)}$[3] - [4].

Mesures du décalage par rapport à la loi log de von Kármán (ligne continue) pour diverses hauteurs de rugosité.

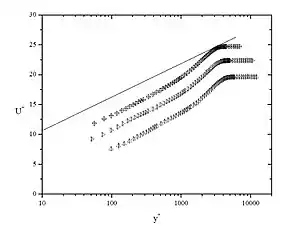
Il n'existe pas de méthode générale permettant de caractériser la rugosité. Dans le cas de rugosités ayant un caractère aléatoire on utilise les caractéristiques statistiques d'une tranche de la surface. Très souvent on utilise des surfaces modèles comme les surfaces avec dépôt de grains de sable comme l'a fait Nikuradzé dans ses expériences historiques ou bien des géométries particulières (hémisphères, troncs de cône...) régulièrement espacées sur une surface plane et qui ont fait l'objet de nombreuses études expérimentales ou numériques[5]. Il existe diverses tentatives essayant de définir une rugosité grain de sable équivalente de ces rugosités discrètes par divers paramètres : espacement, hauteur, aire exposée au vent et projetée sur la surface[6]...

Dans tous les cas on se limite à des rugosités créant des perturbations locales détruites dans la région turbulente, et donc modélisables par un terme ponctuel fonction de y seulement (homogénéisation en x). On distingue trois régimes définis dans le modèle grain de sable de taille ${\displaystyle k}$ par la hauteur adimensionnée ${\displaystyle k^{+}={\frac {ku_{\tau }}{\nu }}}$, ${\displaystyle u_{\tau }}$ étant la valeur sur paroi lisse :

• le régime lisse ${\displaystyle k^{*}\leq 4}$ : les rugosités sont de taille faible devant celle de la sous-couche laminaire et n'entraînent aucun effet ;
• le régime rugueux établi ${\displaystyle k^{*}\geq 70}$ caractérisé par son indépendance au nombre de Reynolds : les effets visqueux sont négligeables et la rugosité modifie localement la pression pariétale dont la valeur moyenne en x comporte alors une composante parallèle à la paroi lisse moyennée du fait des surpressions/dépressions sur chaque obstacle ;
• le régime intermédiaire où les effets sont dus à la pression et au cisaillement.

La structure de la région turbulente de la couche limite n'est pas modifiée par la rugosité et la modification de la région proche de la paroi entraîne un décalage vers le bas (augmentation du cisaillement) de la loi de paroi d'une valeur ${\displaystyle \Delta u^{+}(k^{+})}$ déterminée expérimentalement.

Decomposition de domaine pour une surface périodique. ${\displaystyle \Omega }$ est le domaine physique, ${\displaystyle \Omega _{eq}}$ et ${\displaystyle \Omega _{R}}$ les domaines de calcul effectifs.

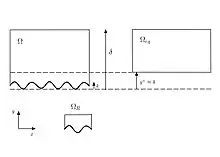
Le terme loi de paroi recouvre également une méthode générale de décomposition de domaine consistant à découper la couche limite en une région visqueuse contenant la rugosité et le reste du domaine. Cette méthode suppose une géométrie périodique qui peut être réalisée artificiellement en utilisant une condition de type Born-von Kármán. Cette méthode est d'usage général et est utilisée en mécanique des fluides pour le problème de la couche de Knudsen ou dans la méthode des développements asymptotiques raccordés pour la couche limite.

Dans le cas général la résolution sera faite numériquement et simultanément dans les deux domaines. Dans certains cas il est possible de paramétrer les résultats du domaine intérieur (échelle mésoscopique) et de construire ainsi une loi numérique qui servira de condition aux limites « effective » pour le domaine extérieur[7] - [8] - [9].

• équation de Hazen-Williams
• équation de Darcy-Weisbach
• Couche limite#Prise en compte de la rugosité
• Écoulement en charge