Loi de Kleiber
La loi de Kleiber[2], formulée par le biologiste Max Kleiber (en) au début des années 1930, énonce que pour la majorité des vertébrés supérieurs, le métabolisme est proportionnel à la masse corporelle élevée à la puissance ¾.
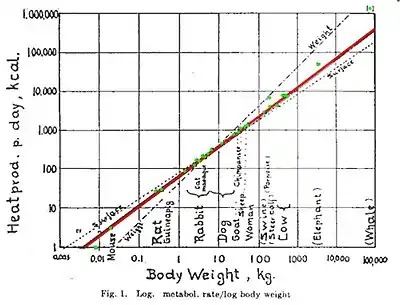
Algébriquement, si l'on convient de noter q0 le métabolisme et M la masse corporelle de l'animal, q04 ~ M3. Ainsi, puisqu'un chat est 100 fois plus lourd qu'une souris, son métabolisme est environ 32 fois plus consommateur d'énergie. Chez les végétaux, par contre, masse et métabolisme sont pratiquement proportionnels.
Biographie
Max Kleiber[3] est né et a été formé à Zürich. Il a été diplômé ingénieur chimiste du Polytechnikum de Zurich en 1920, a soutenu sa thèse de doctorat, consacrée au « Concept d'énergie en diététique », en 1924.
Il travaille à partir de 1929 au département « Domestication animale » de l’université de Californie, chargé de fabriquer des respirateurs artificiels et de mener des recherches sur le métabolisme animal. Il effectue alors deux découvertes importantes : en 1932, comparant les besoins nutritifs de vertébrés de tailles très différentes, il découvre que le métabolisme basal est relié, quelle que soit l’espèce, à la masse de l’animal par une loi de puissance, d’exposant pratiquement égal à ¾. Ses données montrent en outre que le rendement nutritif est indépendant de la taille de l'animal. Il a présenté ces résultats, et exposé les principes fondamentaux du métabolisme dans un essai (inédit en français[4]) The Fire of Life (1961).
Forme algébrique de la loi
La loi de Kleiber, comme d'autres lois biologiques allométriques, résulterait selon certains auteurs[5] - [6] des contraintes physiques imposées par la morphologie du système circulatoire animal. Ainsi les sujets plus jeunes (donc plus petits) respirent davantage d'oxygène par unité de masse corporelle que les sujets adultes de la même espèce à cause des besoins liés à la croissance ; mais les sujets adultes d'une espèce de taille donnée respirent davantage d'oxygène par unité de masse corporelle que les sujets adultes d'une espèce de taille supérieure parce que la part de tissus de structure (os, muscles) est proportionnellement supérieure ; le maintien du squelette et des muscles exige une consommation d'énergie permanente, non les graisses.
Valeur de l'exposant
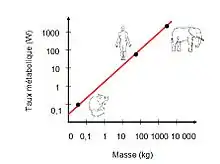
La valeur de l’exposant dans la loi de Kleiber, qui par sa forme est une loi de puissance, a été controversée pendant des décennies : une analyse dimensionnelle simple semblait plutôt justifier une valeur de ⅔. En effet, on considérait que les pertes d'énergie des organismes, mesurées en calories, étaient des pertes sous forme de chaleur : on exprimait alors le métabolisme comme une chaleur dégagée par unité de temps, donc en calories par seconde. Le raisonnement consiste à assigner à tout organisme un « rayon moyen », qui est celui de la sphère ayant même volume que le corps ; et à considérer qu'à l'échelle de l'organisme, la matière corporelle possède une densité homogène. Alors la masse est proportionnelle au cube du rayon moyen, cependant la chaleur est dégagée par la peau, donc proportionnelle à la surface du corps, ou au carré du rayon moyen.
Cette relation explique pourquoi les grands animaux ont une longévité supérieure aux animaux plus petits : ayant une surface spécifique moindre, ils ont un métabolisme plus lent.
Mais la valeur de ⅔ est vraiment trop éloignée de la plupart des données empiriques. Elle est entachée de trop d'exceptions, et le concept de métabolisme était alors encore imprécis, il ne recouvrait que les échanges de chaleur. Kleiber lui-même se convainquit que l'exposant était exactement ¾, et c'est la valeur adoptée aujourd'hui par les partisans de la loi, bien qu'il existe de nombreux contre-exemples dans la nature. Les modèles théoriques présentés par Geoffrey West, Brian Enquist, et James Brown[7] (dits modèles WBE) tendent à justifier l'exposant empirique de ¾ par l'organisation ramifiée des organismes vivants. Leur analyse du cycle métabolique/respiratoire d'un organisme repose entièrement sur des considérations de flux sanguin. Leurs hypothèses ont souvent été mises en cause car les organismes de petite taille ne présentent pas de ramifications aussi complexes que celles prises en compte : la portée des modèles WBE serait limitée aux animaux de plus de 0,002 5 grammes, alors que les auteurs prétendent que la loi de Kleiber est valable aussi bien pour les bactéries (qui n'ont pas de cœur), que pour les baleines.
Concept de rendement métabolique
Les auteurs prétendent que leur modèle tient compte du rendement métabolique ; mais ils aboutissent en fait à une relation de la forme
où ME, appelé « rendement métabolique », incorpore les effets de la température corporelle sur les échanges électrochimiques liés au couplage redox, mais non l'énergie permettant le maintien de cette température. Si l'on accepte ce modèle, une valeur de ¾ ou ⅔, correspond à un rendement de 100 ou 89% ; or, de tels rendements n'existent pas dans la nature, à moins d'inclure la thermogenèse dans le métabolisme. Cette remarque ruine le modèle WBE de la loi de Kleiber, qui fonde la théorie métabolique de l'écologie.
Le métabolisme d'un organisme multicellulaire actif est généralement calculé comme le produit du métabolisme basal moyen par le nombre de cellules de l'organisme[8]. Cette remarque, jointe à l'hypothèse implicite de l'invariance de la taille des plus petits capillaires avec la taille de l'animal, rendent l'équation impuissante à expliquer les pics d'activité métaboliques requis par la locomotion : pour que ces formules soient valables, il faudrait beaucoup plus de sang dans l'organisme qu'on n'en observe en réalité. Pour ces raisons, la loi de Kleiber ne peut avoir de portée universelle en biologie.
Chez les végétaux, l'exposant est voisin de 1, comme l'indique un article paru en 2006 dans Nature[9] - [10], ce que le modèle WBE ne peut expliquer, car il faudrait que ME soit supérieur à 100%.
Problèmes actuels
Les débats scientifiques actuels ne portent plus sur les fondements théoriques de la loi de Kleiber. Le rôle de la thermogenèse dans le métabolisme reste une énigme, en partie parce que la loi de Kleiber, dans sa forme originale, repose sur l'hypothèse que le métabolisme est entièrement une question d'échange de chaleur : on le voit dans le choix de l'unité physique utilisée, la calories/s (au lieu des watts (dans la version de la loi de Kleiber faisant intervenir le rendement métabolique, ME est un rapport de courants redox), ainsi que dans la réduction du débat à la question de savoir si le rendement est de 89 ou de 100%. D’autres chercheurs (par exemple Kozlowski et Konarzewski, ou John Speakman) critiquent West, Brown et Enquist sur l'invariance de taille des capillaires terminaux, supposée identique pour les végétaux et les mammifères : cette hypothèse ne permet pas d'expliquer l'origine de l'énergie requise pour l'activité motrice du sujet[11] - [12]. C'est pourquoi le métabolisme considéré est toujours le métabolisme d'un organisme au repos. West et al. prétendent que la loi de Kleiber vaut pour le métabolisme basal des cellules d'un organisme, et non pour le métabolisme de l'organisme dans son ensemble.
La version standard de l'équation (qui ne fait pas intervenir ME dans l'exposant) n'explique ni les grandes différences de longévité entre les rongeurs et les oiseaux de même poids, ni la longévité des primates par rapport à des mammifères pourtant beaucoup plus lourds.
Notes
- Kleiber M, « Body size and metabolic rate », Physiological Reviews, vol. 27, no 4, , p. 511–541 (PMID 20267758).
- Max Kleiber, « Body size and metabolism », Hilgardia, vol. 6, , p. 315–351 (DOI 10.3733/hilg.v06n11p315).
- Biographical sketch (with photo) of Max Kleiber.
- Cf. le commentaire de Claude Marcel Hladik, Les énergies renouvelables aujourd'hui et demain, Paris, Éditions Ellipses, (lire en ligne), « Le feu de la vie va-t-il consumer la Terre ? », p. 87-102.
- Geoffrey West, James H. Brown et Brian J. Enquist, « A General Model for the Origin of Allometric Scaling Laws in Biology », Science, vol. 276, no 5309, , p. 122–6 (PMID 9082983, DOI 10.1126/science.276.5309.122).
- Robert Shour, « Entropy and its relationship to allometry », sur arxiv 0804.1924, .
- Cf. G.B. West, J.H. Brown, B.J. Enquist, « A general model for the origin of allometric scaling laws in biology », Science, vol. 276, no 5309, , p. 122–6 (PMID 9082983, DOI 10.1126/science.276.5309.122, lire en ligne).
- VM Savage, AP Allen, JH Brown, JF Gillooly, AB Herman, WH Woodruff, GB West, « Scaling of number, size, and metabolic rate of cells with body size in mammals », Proc Natl Acad Sci U S A, vol. 104, no 11, , p. 4718–23 (PMID 17360590, PMCID 1838666, DOI 10.1073/pnas.0611235104, lire en ligne).
- PB Reich, MG Tjoelker, JL Machado, J Oleksyn, « Universal scaling of respiratory metabolism, size, and nitrogen in plants », Nature, vol. 439, no 7075, , p. 457–61 (PMID 16437113, DOI 10.1038/nature04282).
- Cf. « Metabolic Rate and Kleiber's Law », sur A Review of the Universe - Structures, Evolutions, Observations, and Theories (consulté le ).
- J. Kozlowski et M. Konarzewski, « Is West, Brown and Enquist's model of allometric scaling mathematically correct and biologically relevant? », Functional Ecology, vol. 18, no 2, , p. 283–9 (DOI 10.1111/j.0269-8463.2004.00830.x).
- J. Kozlowski et M. Konarzewski, « West, Brown and Enquist's model of allometric scaling again: the same questions remain », Functional Ecology, vol. 19, no 4, , p. 739–743 (DOI 10.1111/j.1365-2435.2005.01021.x, lire en ligne [archive du ]).
Bibliographie
- (en) Rau AR, « Biological scaling and physics », J. Biosci., vol. 27, no 5, , p. 475–8 (PMID 12381870, DOI 10.1007/BF02705043)
- (en) Z. Wang, T. P. O'Connor, S. Heshka et S. B. Heymsfield, « The reconstruction of Kleiber's law at the organ-tissue level », J. Nutr., vol. 131, no 11, , p. 2967–70 (PMID 11694627)
- (en) J. Whitfield, In the Beat of a Heart, Washington, D.C., Joseph Henry Press,
Voir également
- Théorie constructale
- Théorie métabolique de l'écologie
- Lois scalantes
- Dana Mckenzie, « New Clues to Why Size Equals Destiny », The American Association for the Advancement of Science., vol. 284, no 5420, , p. 1607 - 1609 (lire en ligne)
- (en) Thomas Woolley, « 3/4 and Kleiber's Law », Numberphile, Brady Haran

