Accueil🇫🇷Chercher

Liste des groupes de symétrie du plan

Cet article recense les groupes de symétrie du plan euclidien.

Généralités

Les classes considérées sont celles des groupes de symétrie discrets sur le plan euclidien. Il en existe trois sortes :

Ces groupes sont nommés suivant trois nomenclatures : la notation internationale, la notation orbifold et la notation de Coxeter (en).

Liste

Groupes ponctuels

Il existe deux familles de groupes ponctuels discrets bidimensionnels et elles sont spécifiées par le paramètre n, qui est l'ordre du groupe de rotations dans le groupe.

Famille Intl.
(Orbifold)		 Geo
[[1]]
Coxeter		 Schönflies Ordre Exemples
Groupes cycliques n
n•		 n
[n]+
 Cn n
[ ]+
[2]+ (*)
[3]+
[4]+
[5]+
[6]+
Groupes diédraux nm
*n•		 n
[n]
 Dn 2n
[ ]
[2]
[3]
[4]
[5]
[6]

Groupes de frise
UIC
(Orbifold)		 Geo Schönflies Coxeter Domaine
fondamental		 Exemple
p1
(∞•)		 p1 C∞ [∞]+
p1m1
(*∞•)		 p1 C∞v [∞]
p11g
(∞×)		 p.g1 S2∞ [2+,∞+]
p11m
(∞*)		 p. 1 C∞h [2,∞+]
p2
(22∞)		 p2 D∞ [2,∞]+
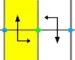p2mg
(2*∞)		 p2g D∞d [2+,∞]
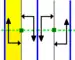p2mm
(*22∞)		 p2 D∞h [2,∞]

Groupes de papier-peint
UIC
(Orbifold)
Géometrique		 Coxeter Réseau Groupe
ponctuel		 Domaine
fondamental		 Exemple
p1
(°)
p1		 [∞+,2,∞+] Oblique C1
p2
(2222)
p2		 [∞,2,∞]+ Oblique C2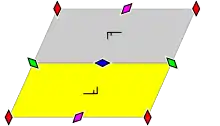
pm
(**)
p1		 [∞+,2,∞]
 Rectangulaire D1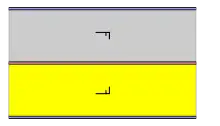
pg
(××)
pg1
 [∞+,(2,∞)+]
 Rectangulaire D1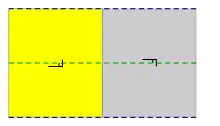
cm
(*×)
c1		 [∞+,2+,∞]
 Losange D1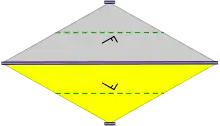
pmm
(*2222)
p2		 [∞,2,∞]
 Rectangulaire D2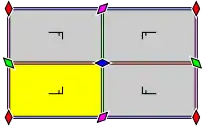
pmg
(22*)
pg2		 [(∞,2)+,∞]
 Rectangulaire D2
pgg
(22×)
pg2g		 [[∞,2,∞]+] Rectangulaire D2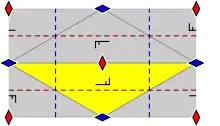
cmm
(2*22)
c2		 [∞,2+,∞]
 Losange D2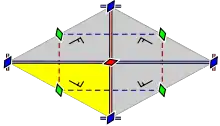
p4
(442)
p4		 [4,4]+
 Carré C4
p4m
(*442)
p4		 [4,4]
 Carré D4
p4g
(4*2)
pg4		 [4+,4]
 Carré D4
p3
(333)
p3		 [1+,6,3+]

[3[3]]+		 Hexagonal C3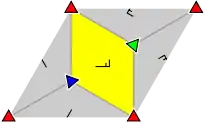
p3m1
(*333)
p3		 [1+,6,3]

[3[3]]
 Hexagonal D3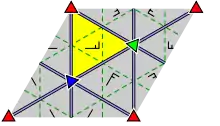
p31m
(3*3)
h3		 [6,3+]

[3+[3[3]]]		 Hexagonal D3
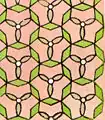p6
(632)
p6		 [6,3]+

[3[3[3]]]+		 Hexagonal C6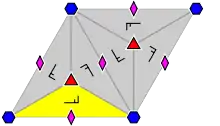
p6m
(*632)
p6		 [6,3]

[3[3[3]]]		 Hexagonal D6

Annexes

Liens externes

Bibliographie
  • (en) John Horton Conway, Heidi Burgiel et Chaim Goodman-Strauss, The Symmetries of Things, A K Peters, , 426 p. (ISBN 978-1-56881-220-5)
  • (en) John Horton Conway et Derek A. Smith, On Quaternions and Octonions, A K Peters, , 160 p. (ISBN 978-1-56881-134-5)
  • (en) F. Arthur Sherk, Peter McMullen, Anthony C. Thompson et Asia Ivic Weiss, Kaleidoscopes : Selected Writings of H.S.M. Coxeter, Wiley-Interscience, , 439 p. (ISBN 978-0-471-01003-6, lire en ligne)
  • (en) Harold Scott MacDonald Coxeter, « Regular and Semi Regular Polytopes I », Mathematische Zeitschrift, vol. 46, no 1,‎ , p. 380-407 (DOI 10.1007/BF01181449)
  • (en) Harold Scott MacDonald Coxeter, « Regular and Semi Regular Polytopes II », Mathematische Zeitschrift, vol. 188, no 4,‎ , p. 559-591 (DOI 10.1007/BF01161657)
  • (en) Harold Scott MacDonald Coxeter, « Regular and Semi Regular Polytopes III », Mathematische Zeitschrift, vol. 200, no 1,‎ , p. 3-45 (DOI 10.1007/BF01161745)
  • (en) David Hestenes et Jeremy Holt, « The Crystallographic Space groups in Geometric algebra », Journal of Mathematical Physics, vol. 48, no 2,‎ (DOI 10.1063/1.2426416)

Références
  1. Hestenes et Holt 2007.
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.