John Smeaton

John Smeaton (8 juin 1724 - 28 octobre 1792) est un ingénieur britannique, souvent surnommé le père du génie civil britannique dans la littérature anglo-saxonne, il est réputé pour sa dextérité et son sens de l'analyse. Il est responsable de la construction de ponts, canaux, ports et de phares. Il est aussi ingénieur en mécanique et physicien. Son nom est associé avec la Lunar Society.

John Smeaton

Biographie
Naissance	8 juin 1724 Austhorpe
Décès	28 octobre 1792 (à 68 ans) Austhorpe
Sépulture	St Mary's Church, Whitkirk (en)
Nationalité	britannique
Formation	Leeds Grammar School (en)
Activités	Ingénieur, physicien, ingénieur mécanicien, ingénieur civil

Autres informations
Membre de	Royal Society
Distinction	Médaille Copley (1759)

Œuvres principales
Coldstream Bridge (d)

Il naît à Austhorpe près de Leeds. Après avoir étudié à la Leeds Grammar School il travaille dans le cabinet juridique de son père.

Le physicien

Il cesse de travailler avec son père pour se lancer dans la fabrication d'instruments scientifiques. Il travaille avec Henry Hindley (en) et développe entre autres un pyromètre, pour étudier l'expansion des matériaux, ainsi qu'un horizon artificiel.

Il est élu membre de la Royal Society en 1753 qui lui décerne la médaille Copley en 1759 pour ses travaux sur les moulins à vent et les norias. Ses papiers explicitent la relation entre la pression et la vitesse des objets se déplaçant dans l'atmosphère.

L'ingénieur

Recommandé par la Royal Society, Smeaton construit le troisième phare d'Eddystone (1755-1759) et met au point un mortier hydraulique basé sur un calcaire mêlé d'argile. Les mortiers hydrauliques deviendront le sujet de préoccupation des constructeurs du XIX^e siècle, et Smeaton sera alors cité comme un précurseur. Ce phare reste en service jusqu'en 1877 date à laquelle il est démantelé et partiellement reconstruit à Plymouth Hoe (en).

Smeaton décide de se consacrer à l'ingénierie civile, plus lucrative, et travaille sur une série d'ouvrages d'art incluant :

La Tour de Smeaton ;
le canal de Calder et Hebber (en) joignant Wakefield et Halifax (1758-1770) ;
le phare de Spurn (1767) ;
le pont de Coldstream au-dessus de la rivière Tweed (1762-1767) ;
l'amélioration du canal de la rivière Lee (1765-1770) ;
le pont de Perth sur la rivière Tray (1766-1770) ;
Le canal Ripon (1766-1773) ;
Le viaduc de Newark-on-Trent sur la rivière Trent dans le Nottinghamshire (1768-1770)
le canal connectant les rivières Forth et Clyde de Grangemouth à Glasgow (1768-1777) ;
le port de Banff (1770-1775) ;
le pont d'Aberdeen (1775-1780) ;
le port de Peterhead (1775) ;
des installations portuaires à Ramsgate (bassin de rétention 1776-1783; jetée 1788-1792) ;
le pont de Hexham (1777-1790) ;
le canal de Birmingham à Fazeley (1782-1789) ;
le port de Sintt Austell à Charlestown en Cornouailles (1792).

Son expérience de l'ingénierie lui vaut d'être cité pour témoigner dans un procès sur l'ensablement du port de Wells-next-the-Sea à Norfolk en 1782. Il est considéré comme le premier expert à avoir été appelé à témoigner lors d'un procès dans une cour de justice anglaise.

Le mécanicien

Il met au point un système d'irrigation utilisant une vis d'Archimède pour les jardins botaniques royaux de Kew en 1761 et un moulin à eau à Alston en Cumbria. Il améliore la machine à vapeur de Thomas Newcomen et en installe une dans une mine de Cornouailles en 1775.

Le mécanicien des fluides (le fameux Coefficient de Smeaton)

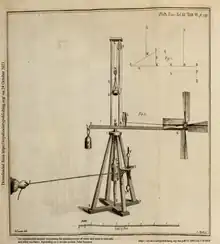
Le dispositif de Smeaton pour la mesure des forces sur un moulin à vent.

La table de Mr. Rouse donnant les efforts sur une plaque dus au vent, citée par Smeaton, 1759

En 1759, John Smeaton publia un texte titré « Une étude expérimentale concernant les pouvoirs naturels de l’eau et de l’air de faire tourner les moulins et autres machines en mouvement circulaire »[1] - [2].

George Cayley commente ainsi le texte de Smeaton et surtout la table de Mr. Rouse[3] qu'y cite Smeaton : « Le résultat des expériences et observations de Mr Smeaton était qu’une surface plane d’un pied carré rencontre une résistance d’une Livre-force quand elle se déplace dans l’air perpendiculairement à elle-même à une vitesse de 21 pieds par seconde »[4].

La plupart des auteurs exprimèrent plutôt, cependant, la vitesse de la surface plane en Miles/heure. À cet aune, ils énonçaient que :

« Une surface plane d’un pied carré rencontre une résistance de 0,005 Livres-force[5] à la vitesse de 1 Mile/h. »

Les dépendances de cette résistance envers le carré de la vitesse relative de l’air et envers la surface de la plaque étant constatées par Smeaton et beaucoup d’autres, le constat précédent pouvait être étendu à toutes les plaques exposées à toutes les vitesses de vent selon la formule :

F=0,005\;S\;V^{2}

pourvu que

F

soit exprimé en Livre-force, que la surface

S

de la plaque soit exprimée en pieds carrés et que la vitesse relative de l’air

V

soit exprimée en Miles/heure.

Pendant 150 ans (jusqu'à l’essor des frères Wright) les chercheurs utilisèrent les concepts et mesures de Smeaton ainsi que cette constante de proportionnalité 0,005 (nommée Coefficient de Smeaton)[6] pour quantifier cette notion basique de pression de Smeaton sur les plaques planes[7] sur des plaques se déplaçant frontalement dans l’air, cette pression (ou plutôt cette surpression) variant comme le carré de la vitesse du fluide.

Il faut noter que ledit Coefficient de Smeaton intègre la Masse volumique de l’air[8]. De même, il faut remarquer que l'antique pression de Smeaton qu'on en tirait fut jugée longtemps comme s’appliquant à l’intégralité de la face avant de la plaque plane exposée au mouvement de l’air[9] - [10].

Mais la valeur 0,005 de ce fameux Coefficient de Smeaton était erronée. Ce constat inquiéta beaucoup les frères Wright qui s’étaient basés dessus pour concevoir leurs premiers planeurs[11] - [12].

Reconstitution de la soufflerie des frères Wright.

Cette déception les incita à effectuer eux-mêmes des mesures d’efforts dans une soufflerie de leur construction[13] - [14]. Par ce moyen, ils purent corriger l’antique Coefficient de Smeaton et lui donner la valeur exacte de 0,003 (valeur que nous calculons ci-dessous).

Démonstration de la vraie valeur du Coefficient de Smeaton

Pendant presque 150 ans, la valeur 0,005 a été admise pour le Coefficient de Smeaton. Ce Coefficient de Smeaton indiquait qu’une surface plane d’un pied carré rencontrait une résistance de 0,005 Livres-force à la vitesse de 1 Mile/h.

Pour connaître la Traînée frontale $F$ d’une plaque quelconque placée dans un vent de vitesse quelconque, on écrivait donc :

$F=0,005\;S\;V^{2}$

…pourvu que $F$ soit exprimé en Livre-force, que la surface $S$ de la plaque soit exprimée en pieds carrés et que la vitesse relative de l’air $V$ soit exprimée en Miles/heure.

Comme une Livre-force équivaut à 4,448 Newton, la traînée d’une surface plane d’un pied carré à un Mile/heure équivaut à 0,005*4,448 Newton, soit 0,0222 N.

Calculons à présent la traînée exacte[15] de cette plaque d’un pied carré à un Mile/heure avec nos équations et unités scientifiques modernes :

On sait cette traînée $F$ donnée par l’équation :

$F={\frac {1}{2}}\;\rho \;V^{2}\;S\;C_{x}$

Comme un pied carré équivaut à 0,093 m² et qu’un Mile/h équivaut à 0,447 m/s, on peut écrire, en prenant 1,225 Kg/m³ pour la Masse volumique de l’air[16] et en adoptant un $C_{x}$ de 1,19 pour la plaque plane[17] :

$={\frac {1}{2}}\;1,225\;(0,447m/s)^{2}\;0,093m^{2}\;1,19=0,0135\;N$

On remarque que cette traînée moderne est plus faible que celle déterminée par l’antique Coefficient de Smeaton. Elle est 0,61 fois plus faible. Ce qui signifie que le Coefficient de Smeaton est trop fort. Il devrait être pris à 0,61*0,005, soit 0,003.

Cette valeur de 0,003 fut celle dégagée à l’issue de leurs essais par les frères Wright[8].

Ses legs

Il est très estimé par les autres ingénieurs. Il contribue activement à la Lunar Society, une sorte de club de discussion réunissant ingénieurs, scientifiques et industriels. Il invente le terme de civil engineering -- génie civil, pour le distinguer de l'ingénierie militaire et des grands corps de l'état. Il fonde la Society of Civil Engineers en 1771 qui est renommé Smeaton Society après sa mort, société savante ancêtre de l'Institution of Civil Engineers en 1818.

Ses élèves incluent les constructeurs de canaux James Brindley et William Jessop et l'architecte et ingénieur Benjamin Latrobe.

Il meurt d'une attaque tandis qu'il marche dans les jardins familiaux à Austhorpe et est enterré dans la paroisse de Whitkirk (en).

Bibliographie

(en) John Smeaton, FRS, A W Skempton, 1981, (ISBN 072770088X)
Biographie succincte
(en) Les ouvrages d'art de Smeaton
(en) Jennifer Karns Alexander, « Static and dynamic efficiency : The waterwheels of Smeaton and the Franklin institute », dans The mantra of efficiency: From waterwheel to social control, JHU Press, 2008, p. 15 (ISBN 0801886937 et 9780801886935). Extraits en ligne sur Google livres

Notes et références

Mr J Smeaton, « An Experimental Enquiry concerning the Natural Powers of Water and Wind to Turn Mills, and Other Machines, Depending on a Circular Motion. », Philosophical Transactions of the Royal Society, vol. 51,‎ 1759, p. 100–174 (DOI 10.1098/rstl.1759.0019 )
Peter L. Jakob, Visions of a Flying Machine, Washington and London: Smithsonian Institution, 1990 : cité dans :
Smeaton présente Mr. Rouse comme son ami et comme « un gentleman ingénieux d’Harborough, dans le Leicestershire, ayant construit un manège d’essais (dispositif à bras tournant) pour la mesure des plaques planes et des voilures de moulin à vent.
The Wind and Beyond: A Documentary Journey into the History of Aerodynamics in America, Volume 1: The Ascent of the Airplane, James R. Hansen, Editor | https://history.nasa.gov/SP-4409%20vol1.pdf
La Livre-force, sur le modèle du Kilogramme-force, est le poids que pèse une Livre sur notre planète, la Livre étant une unité de masse et non de force.
Cette constante était nommée « Coefficient de Smeaton » bien qu'elle ait été tirée des mesures d’un certain Mr. Rouse
En fait c'est une surpression, la surpression créée par le mouvement relatif du fluide sur le corps.
On découvrit plus tard que le fluide,pour contourner la plaque, est obligé d’accélérer en s’approchant des bords de la plaque, ce qui, en application du l’équation de Bernoulli conduit à une diminution importante de sa surpression spécialement sur les bords de la plaque où elle peut être négative. Les anciens auteurs ignoraient également la dépression existant à l'aval (ou culot) de la plaque (dépression de culot découverte par Pierre du Buat.), cette dépression augmentant la traînée et venant diminuer l'effet de l'accélération du flux sur la face amont (voir à ce sujet l'image les mesures de pressions de Stanton citées par Eiffel montrant la répartition des pressions sur diverses plaques).
Pour ces notions de pression et de surpression, voir l’article Coefficient de pression
Le planeur de 1901 des frères Wright avait été conçu pour soulever son propre poids (100 Livres-force) plus celui d’un pilote (150 Livres-force) quand il était utilisé comme un cerf-volant à 5 degrés d’incidence dans un vent de 15 Miles par heure. Mais il s’avéra que ce planeur pouvait difficilement soulever son propre poids dans un tel vent de 15 M/h et encore avec une incidence plus forte.
Smeaton Coefficient, Glenn Research Center, https://wright.nasa.gov/airplane/smeaton.html
Centennial of Flight Commision,
Ce fut sans doute la deuxième soufflerie des États-unis, mise en service quelques mois après celle de Zham. Si la soufflerie de frère Wright mesurait 1,8 m de long et sa section d'essais carrée 40 cm , celle de Zham, mesurait cependant 12,2 m de long et sa section d’essais carrée 1,8 m (Zham fut plus tard l’un des fondateurs du NACA, ancêtre de la NASA).
Nous utilisons l’expression traînée exacte pour signifier la traînée que calculerait, en première intention, un ingénieur moderne.
1,225 est la Masse volumique de l'air sec au niveau de la mer sous une pression de 1 013,25 hPa. Voir à ce sujet l'article Masse volumique de l'air. Bien sûr ce calcul peut être fait avec d'autres valeurs pour la Masse volumique de l'air.
Le $C_{x}$ d’une plaque plane exposée frontalement n’évolue pas beaucoup lorsque son rapport longueur / largeur varie : Le $C_{x}$ de la plaque carrée vaut 1,18 alors que celui d’un plaque de rapport longueur/largeur = 5 vaut 1,2 ; cette relativement faible variation rendait assez réaliste l’assimilation par Smeaton et ses successeurs de toutes les plaques planes à une plaque plane moyenne.

Liens externes

Notices d'autorité :
- VIAF
- ISNI
- BnF (données)
- IdRef
- LCCN
- GND
- Espagne
- Belgique
- Pays-Bas
- Tchéquie
- Portugal
- WorldCat
Notices dans des dictionnaires ou encyclopédies généralistes :
Ressources relatives aux beaux-arts :
- Royal Academy of Arts
- (en) Art UK
- (en) British Museum
- (en) Grove Art Online
- (en) National Gallery of Art
- (en) National Portrait Gallery
- (en) Union List of Artist Names
Ressource relative à l'architecture :
- (en) Dictionary of Scottish Architects

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.