Instabilité de Plateau-Rayleigh

L’instabilité de Plateau-Rayleigh est nommée d’après les physiciens belges Joseph Plateau et britannique Lord Rayleigh pour leurs contributions à l’étude de ce phénomène. En 1873, Plateau détermine expérimentalement qu'un fluide qui tombe verticalement se scinde en gouttes si sa longueur d’onde est plus grande que 3,13 à 3,18 fois son diamètre et remarque que cette valeur est proche de π[3] - [4]. Par la suite, Rayleigh montre théoriquement qu’une colonne de liquide non visqueux de section circulaire tombant verticalement doit se scinder en gouttes si sa longueur d’onde dépasse sa circonférence, qui vaut alors π fois son diamètre[5].

Étape intermédiaire d’un écoulement se séparant en gouttes. Les rayons de courbure dans la direction axiale sont visibles. L’expression du rayon de l’écoulement est ${\displaystyle R(z)=R_{0}+A_{k}\cos(kz)}$, où ${\displaystyle R_{0}}$ est le rayon de l’écoulement non perturbé, ${\displaystyle A_{k}}$ est l’amplitude de la perturbation, ${\displaystyle \scriptstyle z}$ est la distance le long de l’axe de l’écoulement, et ${\displaystyle k}$ est le nombre d’onde.

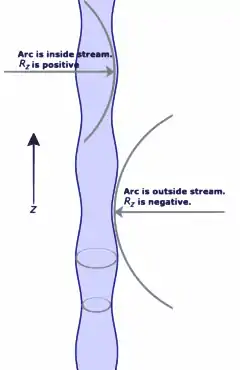
L'instabilité s'explique en premier lieu par l’existence de minuscules perturbations dans l'écoulement[6] - [7]. Elles sont toujours présentes, quelle que soit la régularité de l'écoulement (par exemple, dans une buse, il y a une vibration de l'écoulement à cause de la friction entre la buse et le liquide). Si ces perturbations prennent la forme de composantes sinusoïdales, on détermine que certaines d'entre-elles sont amplifiées au cours du temps, alors que d’autres sont atténuées. Parmi celles qui sont amplifiées, certaines le sont plus rapidement que les autres. L’amplification ou l’atténuation et la vitesse de croissance d’une composante sont entièrement déterminées par son nombre d’onde (qui mesure le nombre d’oscillations par unité de longueur) et le rayon initial de l'écoulement. Le diagramme de droite montre une unique composante de manière exagérée.

En supposant qu’initialement toutes les composantes possibles existent avec de petites amplitudes à peu près similaires, la taille des gouttes peut être prédite en déterminant quelle composante croît le plus pour chaque nombre d’onde. À mesure que le temps passe, la composante dont la vitesse de croissance est la plus élevée finira par dominer et séparer l'écoulement en gouttes[8].

Le diagramme permet de comprendre le principe général, bien qu’un développement mathématique soit nécessaire pour comprendre en détails comment cela se produit (voir [6] - [8]). On y observe deux bandes entourant l'écoulement – une sur un sommet et l’autre à un creux de l’onde. Au creux de l’onde, le rayon de l'écoulement est plus petit et donc, d’après l’équation de Laplace-Young, la pression due à la tension superficielle est augmentée. Similairement, le rayon au sommet de l’écoulement est plus grand et, par le même raisonnement, la pression due à la tension superficielle est réduite. Si c’était le seul effet en jeu, on s’attendrait à ce que la pression supérieure dans le creux presse le liquide dans la région de pression inférieure au niveau des sommets. On comprend ainsi comment l’amplitude de l’onde croît au cours du temps.

Néanmoins, l’équation de Laplace-Young est influencée par deux types de rayons différents. Un est le rayon de l’écoulement lui-même, comme déjà discuté. L’autre est le rayon de courbure de l’onde elle-même. Les arcs épousant l'écoulement sur le diagramme montrent deux valeurs du rayon de courbure au niveau des sommets et des creux. On observe que le rayon de courbure au niveau du creux est en vérité négatif, ce qui signifie, d’après l’équation de Young-Laplace, qu’il contribue en fait à la diminution de la pression dans le creux. De manière analogue, le rayon de courbure au niveau du sommet est positif et augmente la pression dans cette région. L’effet de ces contributions s’oppose à l’effet lié au rayon de l’écoulement lui-même.

En général, les deux phénomènes ne s’annulent pas exactement. Un des deux sera d'une intensité supérieure à l'autre, en fonction du nombre d’onde et du rayon de l'écoulement. Quand le nombre d'onde est tel que l'effet du rayon de courbure de l'onde domine celui du rayon de l'écoulement, la perturbation associée sera atténuée au cours du temps. Quand l'effet du rayon de l'écoulement domine celui du rayon de courbure de l'onde, la perturbation associée sera amplifiée exponentiellement au cours du temps.

Un développement mathématique permet de conclure que les composantes instables (c'est-à-dire celles qui croissent au cours du temps) sont exactement celles pour lesquelles le produit du rayon initial et du nombre d'onde est inférieur à un (${\displaystyle kR_{0}<1}$). La composante qui croît le plus vite est celle dont le nombre d'onde satisfait l'équation[8]

${\displaystyle kR_{0}\simeq 0.697.}$