Force d'inertie

Forces subies par une voiture accélérée (masse M), son siège (masse négligeable) et son conducteur (masse m) dans un référentiel galiléen (en haut et au milieu) et dans leur propre référentiel accéléré (en bas). Dans le référentiel galiléen, ils sont soumis à des forces dont la résultante, non nulle, leur confère une accélération a. Dans leur propre référentiel, les forces d'inertie d'entraînement −Ma et −ma équilibrent les autres forces et leur permettent de rester au repos.

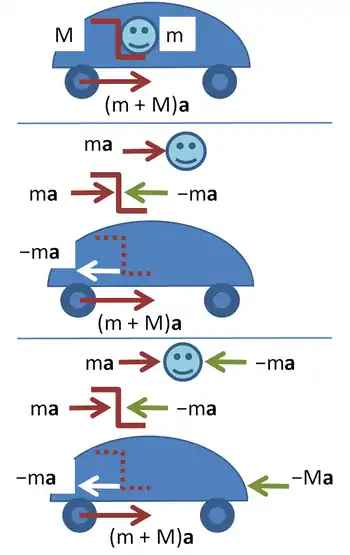
La figure ci-contre illustre le cas d'une voiture qui accélère en ligne droite. On peut comparer le point de vue d'un piéton, supposé galiléen, qui observe depuis le trottoir, à celui de l'automobiliste :

• du point de vue du piéton (figure d'en haut), le frottement statique des roues sur la chaussée imprime au véhicule une accélération a. La force en question vaut (m+M)a, où M et m sont les masses respectives de la voiture et de son conducteur ;
• la figure du milieu représente le même point de vue, mais en considérant séparément la voiture, le siège (supposé de masse négligeable) et le conducteur. Ce dernier est accéléré par une force ma en provenance du siège, alors que la voiture reçoit une force (m+M)a de la chaussée et −ma du siège ;
• la figure du bas représente le point de vue non galiléen du conducteur. Celui-ci ressent une force d'inertie −ma qui le plaque vers l'arrière, ainsi que la réaction +ma de son siège qui le retient. La résultante est nulle et le conducteur est au repos dans son propre référentiel. La voiture subit la force d'inertie −Ma, l'action du siège −ma et l'action de la chaussée (m+M)a : la résultante est encore nulle et elle reste au repos.

Dans les deux cas, les forces d'interaction chaussée/voiture, voiture/siège et siège/conducteur sont les mêmes : ce sont les « vraies » forces, indépendantes du référentiel. On peut remarquer que les forces d'inertie servent ici à équilibrer ces forces afin de maintenir l'automobiliste et sa voiture au repos dans leur propre référentiel.

La force d'inertie, pour la plupart des dictionnaires, est la résistance des corps au mouvement, résistance proportionnelle à leur masse.

Soit (R) un référentiel galiléen centré en 0, et (R') un référentiel non galiléen centré en A, dont la rotation (instantanée) autour de (R) est donnée par le vecteur ${\displaystyle {\vec {\Omega }}_{(\mathrm {R'/R} )}}$. Soit un point M mobile de masse m subissant des forces de résultante ${\displaystyle {\vec {\mathrm {F} }}}$. Soit ${\displaystyle {\vec {v}}_{\mathrm {r} }={\vec {v}}(\mathrm {M} )_{(\mathrm {R'} )}}$ la vitesse relative de M dans (R').

Alors, d'après la loi de composition des mouvements, en notant ${\displaystyle {\vec {a}}_{\mathrm {a} }}$ l'accélération absolue dans (R), ${\displaystyle {\vec {a}}_{\mathrm {r} }}$ l'accélération relative dans (R'), ${\displaystyle {\vec {a}}_{\mathrm {e} }}$ l'accélération d'entraînement et enfin ${\displaystyle {\vec {a}}_{\mathrm {c} }}$ l'accélération de Coriolis, on a :

${\displaystyle {\vec {a}}_{\mathrm {a} }={\vec {a}}_{\mathrm {r} }+{\vec {a}}_{\mathrm {e} }+{\vec {a}}_{\mathrm {c} }}$

Or, d'après le principe fondamental de la dynamique, on a : ${\displaystyle m\ {\vec {a}}_{\mathrm {a} }={\vec {\mathrm {F} }}}$

D'où, dans (R'): ${\displaystyle m{\vec {a}}_{\mathrm {r} }={\vec {\mathrm {F} }}-m{\vec {a}}_{\mathrm {e} }-m{\vec {a}}_{\mathrm {c} }}$

En définissant les forces d'inertie ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ie} }=-m{\vec {a}}_{\mathrm {e} }}$ et ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ic} }=-m{\vec {a}}_{\mathrm {c} }}$, on peut alors écrire le principe fondamental de la dynamique dans le référentiel (R') non galiléen :

${\displaystyle m{\vec {a}}_{\mathrm {r} }={\vec {\mathrm {F} }}+{\vec {\mathrm {F} }}_{\mathrm {ie} }+{\vec {\mathrm {F} }}_{\mathrm {ic} }}$

La force ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ie} }}$ est appelée force d'inertie d'entrainement, et son expression développée est :

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ie} }=-m{\vec {a}}_{\mathrm {e} }=-m\left[{\vec {a}}(\mathrm {A} )_{(\mathrm {R} )}+\left({\frac {\mathrm {d} {\vec {\Omega }}_{(\mathrm {R'/R} )}}{\mathrm {d} t}}\right)_{(\mathrm {R} )}\wedge {\overrightarrow {\mathrm {AM} }}+{\vec {\Omega }}_{(\mathrm {R'/R} )}\wedge ({\vec {\Omega }}_{(\mathrm {R'/R} )}\wedge {\overrightarrow {\mathrm {AM} }})\right]}$

Dans l'expression précédente :

• le terme ${\displaystyle -m\left[\left({\frac {\mathrm {d} {\vec {\Omega }}_{(\mathrm {R'/R} )}}{\mathrm {d} t}}\right)_{(\mathrm {R} )}\wedge {\overrightarrow {\mathrm {AM} }}\right]}$ est la force d'Euler[1] ;
• le terme ${\displaystyle -m\left[{\vec {\Omega }}_{(\mathrm {R'/R} )}\wedge ({\vec {\Omega }}_{(\mathrm {R'/R} )}\wedge {\overrightarrow {\mathrm {AM} }})\right]}$ est la force centrifuge[2] (ou axifuge).

La force ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ic} }}$ est appelée force d'inertie de Coriolis, et son expression développée est :

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ic} }=-m{\vec {a}}_{\mathrm {c} }=-m2{\vec {\Omega }}_{(\mathrm {R'/R} )}\wedge {\vec {v}}_{\mathrm {r} }}$

Dans une première approche de la mécanique newtonienne, on peut définir le mot force de la manière suivante. Une force :

• est la modélisation d'une interaction, c'est-à-dire de l'action d'un objet sur un autre ; c'est le cas en particulier des interactions de contact (pression, frottement, interaction dans une liaison) ou à distance (force gravitationnelle, force électrostatique, force électromagnétique) ;
• respecte le principe des actions réciproques (troisième loi de newton).

Comme une force d'inertie ne respecte ni l'une ni l'autre de ces conditions, elles peuvent parfois être considérées comme des forces fictives ou pseudo-forces. Il faut toutefois noter les éléments suivants :

• les interactions électromagnétiques ne respectent pas le principe des actions réciproques dès que l'on ne se place plus dans le cadre de la statique ;
• la force de gravitation est de même nature que les forces d'inertie. Il n'est donc pas possible de distinguer expérimentalement dans le poids d'un objet la composante due à la gravitation (considérée comme une force réelle) et la composante due à la rotation de la Terre (considérée comme une force fictive).

Certains auteurs utilisent plutôt les termes d'accélération centrifuge, accélération inertielle et effet de Coriolis[3] pour désigner les causes de ce que d'autres nomment respectivement force centrifuge, force inertielle et force de Coriolis[4].

La notion de force d'inertie apparaît en relativité générale[5] - [6]. Les forces d'inertie sont toujours proportionnelles à la masse de l'objet sur lequel elles agissent, ce qui est aussi le cas de la gravité. Ceci a conduit Albert Einstein à se demander si la gravitation était aussi une force d'inertie. Il remarque qu'un observateur en chute libre dans une pièce fermée ne ressent pas la gravité, et peut se croire dans un référentiel inertiel (c'est le principe d'équivalence). Ceci a conduit Einstein à formuler une théorie où la gravitation est une pseudo-force due à la courbure de l'espace-temps. Cette idée est le fondement de la relativité générale.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Fictitious force » (voir la liste des auteurs).

• Force de Coriolis
• Force centrifuge
• Référentiel non inertiel
• Composition des mouvements