Fonction de localisation électronique

La dérivation originale faite par A. Becke et K. Edgecombe considère comme critère de localisation la probabilité de présence d’un électron de spin ${\displaystyle \sigma }$ à l’intérieur d’un petit volume sphérique, V, centré en r position occupée par l’ électron de référence de même spin. Cette quantité ${\displaystyle D_{\sigma }(\mathbf {r} )}$ est obtenue en intégrant la probabilité conditionnelle, ${\displaystyle P_{\mathrm {cond} }^{\sigma \sigma }(\mathbf {r} ,\mathbf {r} ^{\prime })=\Pi ^{\sigma \sigma }(\mathbf {r} ,\mathbf {r} ^{\prime })/\rho ^{\sigma }(\mathbf {r} )}$ sur le volume ${\displaystyle V}$:

${\displaystyle D_{\sigma }(\mathbf {r} )=\int \limits _{V}P_{\mathrm {cond} }^{\sigma \sigma }(\mathbf {r} ,\mathbf {r} ^{\prime })d\mathbf {r} ^{\prime }}$

Dans l'expression de la probabilité conditionnelle ${\displaystyle \Pi ^{\sigma \sigma }(\mathbf {r} ,\mathbf {r} ^{\prime })d\mathbf {r} ^{\prime }}$ est la probabilité de paire, celle de trouver deux électrons de même spin en ${\displaystyle \mathbf {r} }$ et ${\displaystyle \mathbf {r} ^{\prime }}$ et ${\displaystyle \rho ^{\sigma }(\mathbf {r} )}$ la probabilité de trouver un électron de spin ${\displaystyle \sigma }$ en ${\displaystyle \mathbf {r} }$. Les valeurs de ${\displaystyle D_{\sigma }(\mathbf {r} )}$ sont très faibles dans les régions dominées par la présence d’un seul électron du spin considéré et deviennent plus importantes dès lors qu’un second électron de même spin est susceptible de se trouver au voisinage de l’électron de référence. Ce comportement est illustré par la figure représentant ${\displaystyle D_{\sigma }(\mathbf {r} )}$ le long du segment joignant deux noyaux d'hélium dans l’état fondamental .

${\displaystyle D_{\sigma }(\mathbf {r} )}$ le long du segment joignant les noyaux de deux atomes d'hélium dans l'état fondamental, la probabilité conditionnelle intégrée est maximale à mi-distance.

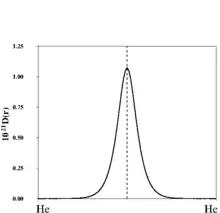
Becke et Edgecombe ont utilisé une expression approchée de ${\displaystyle D_{\sigma }(\mathbf {r} )}$ obtenue en considérant le premier terme non nul du développement de Taylor de la probabilité conditionnelle dans l’approximation Hartree-Fock. Le volume de la sphère étant arbitraire, l’expression approchée de ${\displaystyle D_{\sigma }(\mathbf {r} )}$ est divisée par son équivalent calculé pour un système de référence, le gaz homogène d’électron de même densité, ${\displaystyle D_{\sigma }^{0}(\mathbf {r} )}$. Le rapport ainsi obtenu est finalement réécrit sous une forme lorentzienne :

${\displaystyle ELF(\mathbf {r} )={\frac {\displaystyle 1}{\displaystyle 1+\left({\frac {D_{\sigma }(\mathbf {r} )}{D_{\sigma }^{0}(\mathbf {r} )}}\right)^{2}}}}$

Les valeurs de ELF sont comprise entre 0 et 1, les valeurs élevées de ELF correspondant aux régions de «forte localisation». La formule de Becke et Edgecombe a inspiré de nombreuses interprétations parmi lesquelles celle proposée par Andréas Savin et al.[2] où ${\displaystyle D_{\sigma }}$ est assimilé à l'excès local d'énergie cinétique dû à la répulsion de Pauli. Cette reformulation généralise la formule de Becke et Edgecombe à la théorie de la fonctionnelle de la densité (DFT). Il existe d'autres généralisations permettant de calculer ELF à partir de densités «expérimentales»[3], de fonctions d'onde corrélées[4], de la DFT quasi-relativiste (SODFT)[5] ainsi qu'une expression de ELF dépendant du temps[6].

ELF est une fonction totalement symétrique et, dans le cas de fonctions d'ondes approchées exprimées à l'aide d'orbitales, ELF est invariant par rapport à toute transformation unitaire de ces dernières. En pratique la fonction ELF est exprimée sous une forme analytique dans la mesure où elle est évaluée à partir de fonctions d'onde approchées utilisant des orbitales ayant elles-mêmes une expression analytique. ELF est une grandeur sans dimension qui doit être considéré comme un indicateur de localisation plutôt que comme une mesure de la localisation, qui elle impliquerait l'existence d'un opérateur spécifique.

Couches électroniques de l'atome de xénon. À gauche, la densité électronique dans le plan de l'image est représentée par un nuage de points colorés en fonction de la valeur de ELF; au centre, profil radial de ELF; à droite profil de ELF en fonction de la densité intégrée ${\displaystyle Q(r)=\int _{r}\rho (\mathbf {r} )d\mathbf {r} }$. Les lignes verticales correspondent à la somme des occupations du modèle orbitalaire, ici 2, 10, 28, 46.

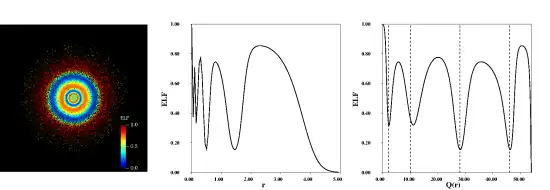
Les premières applications en chimie quantique, essentiellement qualitatives, ont été réalisées sur des atomes, de petites molécules et des systèmes cristallins simples. Les diverses techniques de visualisation mettent clairement en évidence les régions de l’espace où sont attendues les couches atomiques, les liaisons chimiques covalentes et les paires libres. Les représentations proposées par ELF sont cohérentes avec la théorie de la valence de Lewis et avec le modèle VSEPR. De surcroit la fonction ELF s'est avérée être l'une des rares méthodes capables de distinguer la couche de valence des atomes au-delà de la troisième période.

La partition de l’espace moléculaire et les bassins de ELF

Représentation ELF de la molécule de furane. À gauche: nuage de points dans le plan des noyaux colorés selon la valeur de ELF; à droite: domaines de localisation déterminés par l'isosurface ${\displaystyle ELF(\mathbf {r} )=0.8}$, le code couleur est celui de l'ordre synaptique des bassins dont dépendent les domaines de localisation.

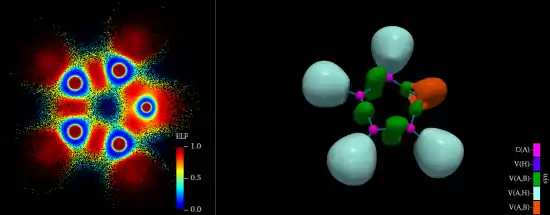
La partition de l’espace moléculaire est réalisée en considérant les bassins des attracteurs du système dynamique gradient de la fonction ELF. Les attracteurs sont les maxima locaux et les bassins des volumes séparés par des surfaces de flux nul (${\displaystyle \nabla ELF(\mathbf {r} )=0}$. Cette stratégie est inspirée de la théorie quantique des atomes dans les molécules (QTAIM) de Richard Bader. Les bassins de ELF ont une signification chimique claire en fonction de leur position par rapport aux noyaux: les bassins de cœur sont situés autour des noyaux de numéro atomique supérieurs à 2 tandis que le reste de l’espace est occupé par les bassins de valence. Dans l’approche ELF un atome dans une molécule est constitué du noyau, des bassins de cœur correspondant aux couches internes et des bassins de valence entourant la dernière couche de cœur. Dans la pratique les couches de cœur d’un même atome A sont regroupées en un super bassin noté C(A). Un même bassin de valence peut appartenir aux couches de valence de plusieurs atomes, l’ordre synaptique d’un bassin est le nombre de couches de valence auquel il appartient, il existe ainsi des bassins monosynaptiques V(A) pour les paires libres, des bassins disynaptiques V(A,B) pour les liaisons bicentriques covalentes ou datives A-B et des bassins polysynaptiques pour les liaisons multicentriques. Comme QTAIM, l’approche ELF distingue deux types principaux d’interactions, celles avec partage de densité électronique (liaison covalente, métallique et datives) et celles sans partage (liaison ioniques, liaison hydrogène, etc.))[7]. L’introduction des domaines de localisation (volumes limités par une isosurface) permet une représentation graphique claire comme le montre la figure représentant la molécule de furane.

D'un point de vue quantitatif, l’intégration sur les bassins des densités de probabilité permet de calculer les populations de bassin : électroniques de spin ${\displaystyle \alpha }$ et ${\displaystyle \beta }$ et totales, de paires électroniques de même spin, de spins opposés et totales, ainsi la matrice des covariances des populations de bassin qui mesure les fluctuations de la densité électronique des bassins et leur corrélation. Les populations calculées par cette méthode sont le plus souvent en très bon accord avec les valeurs prévues par le modèle de Lewis à l’exception des systèmes qui, comme le benzène, ne pouvant être décrit par une structure unique, nécessitent l’introduction de formes mésomères.

• (en) Frank R. Wagner (ed.) Electron localizability: chemical bonding analysis in direct and momentum space. Max-Planck-Institut für Chemische Physik fester Stoffe, 2002. (accédé le 2 décembre 2009).
• (fr) « Regards d'ELFe », film scientifique sur les fonctions ELF.