Fonction à trappe
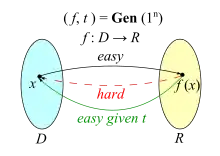
En cryptologie, une fonction à trappe ou TDF (pour l'anglais trapdoor function) est un modèle idéalisé permettant de raisonner à propos de systèmes cryptographiques. En première approche, il s'agit d'une fonction qu'il est facile d'évaluer en chaque point de son domaine, mais qu'il est difficile d'inverser à moins de disposer d'une information particulière, appelée « trappe »[Note 1].
Histoire
La notion de fonction à trappe a été introduite par les cryptologues américains Whitfield Diffie et Martin Hellman en 1979[1], comme une manière de résoudre le problème de la cryptographie à clé publique tel que posé par Ralph Merkle quelques années plus tôt[2] - [Note 2]. Étant donné une fonction à trappe, il est en effet immédiat de construire un algorithme de chiffrement ou de signature numérique. Cependant Diffie et Hellman ne proposent pas de telle fonction dans leur article[1].
La question de l'existence de fonctions à trappes a été difficile, le premier exemple pratique étant dû à Rivest, Shamir et Adleman en 1976[3] - [Note 3] - [4] et reposant sur le problème RSA. C'est en partie pour ces travaux que les trois reçoivent en 2002 le prestigieux prix Turing. En 1979 Michael Rabin a proposé montrer comment construire une fonction à trappe reposant sur le problème de la factorisation[5]. Dans les deux cas, RSA et Rabin, la trappe est donnée par un facteur d'un grand nombre composé.
Dans les années qui suivirent, les progrès en cryptologie (dus notamment à Lamport, Goldwasser-Micali-Rivest, Goldreich-Goldwasser-Micali, Goldreich, Naor-Yung, Rompel[6] et d'autres) ont montré comment construire des algorithmes de signature simplement à partir de fonctions à sens unique, relativisant grandement l'intérêt des fonctions à trappes[6] - [7]. Ainsi par exemple, les signatures ECDSA reposent sur le problème du logarithme discret, pour lequel aucune trappe n'est connue. Construire génériquement un chiffrement à clé publique à partir de fonctions à sens unique uniquement est interdit par un résultat de séparation dû à Impagliazzo et Rudich[8], et on ignore (en 2018) si combiner les fonctions à sens unique et les permutations pseudo-aléatoires suffit[7]. Cela dit, il existe des constructions ad hoc telles que le chiffrement d'ElGamal ou de Cramer-Shoup reposant sur le logarithme discret[Note 4].
Comme mentionné plus haut, une fonction à trappe donne immédiatement un schéma de chiffrement à clé publique. Cependant il n'est pas possible de construire génériquement une fonction à trappe à partir d'un chiffrement à clé publique[9], les deux notions étant séparées en boîte noire.
Un regain d'intérêt pour les fonctions à trappe est apparu avec le développement de la cryptographie à base de réseaux[10] - [11] - [12] - [13] où la trappe est généralement donnée par une « bonne base » d'un réseau euclidien.
Définition
Une collection de fonctions à trappe est la donnée d'un ensemble de fonctions satisfaisant les trois propriétés suivantes[7] :
- Il existe un algorithme efficace[Note 5] de « génération » qui prend en entrée un paramètre de sécurité en représentation unaire et produit une paire[Note 6] de fonctions de ;
- Il existe un algorithme efficace d'« échantillonnage » , c'est-à-dire un algorithme qui prend en entrée et retourne un élément aléatoire de , distribué de façon uniforme[Note 7] ;
- La fonction obtenue en sortie de est à sens unique, c'est-à-dire que pour tout adversaire efficace il existe une fonction négligeable telle que
Une définition moins générale mais plus proche des constructions consiste à supposer que toutes les fonctions ont même domaine, i.e. et que ce domaine est représentable i.e. [14].
On peut également demander que les fonctions de soient des permutations (auquel cas ), et on parle alors de « permutations à trappe ». À l'heure actuelle (2018) la seule construction connue susceptible de donner une permutation à trappe repose sur le problème RSA ou une variante mineure de celui-ci[14].
Notes et références
Notes
- Pour que la notion ne soit pas creuse, il faut bien entendu que la trappe ne soit pas elle même facile à calculer à partir d'une représentation de la fonction.
- Les puzzles de Merkle sont un premier pas dans cette direction, mais la difficulté d'inverser le problème reste quadratique (i.e. polynomiale) alors qu'une fonction à trappe exige un avantage négligeable (i.e. exponentiel).
- Voir aussi Ron Rivest, The early days of RSA.
- Nécessairement, ces constructions utilisent davantage que le sens unique de l'exponentiation modulaire.
- Généralement, une machine de Turing probabiliste.
- Précisément : il s'agit d'une paire de chaînes de caractères, de taille au plus polynomiale en , décrivant les fonctions et .
- C'est-à-dire que l'avantage d'un adversaire à distinguer la distribution effective des éléments ainsi obtenu d'une distribution uniforme est négligeable.
Références
- (en) W. Diffie et M. Hellman, « New directions in cryptography », IEEE Transactions on Information Theory, vol. 22, no 6, , p. 644–654 (ISSN 0018-9448, DOI 10.1109/TIT.1976.1055638, lire en ligne, consulté le )
- (en) Ralph Merkle, "Secure Communication Over Insecure Channels", 1975
- R. L. Rivest, A. Shamir et L. Adleman, « A method for obtaining digital signatures and public-key cryptosystems », Communications of the ACM, vol. 21, no 2, , p. 120–126 (ISSN 0001-0782, DOI 10.1145/359340.359342, lire en ligne, consulté le )
- (en) Rivest, Shamir et Adleman, Cryptographic communications system and method, (lire en ligne)
- (en) M. O. Rabin, « Digitalized Signatures and Public-Key Functions as Intractable as Factorization », Technical Report, MIT, (lire en ligne, consulté le )
- (en) J. Rompel, « One-way functions are necessary and sufficient for secure signatures », STOC '90 Proceedings of the twenty-second annual ACM symposium on Theory of computing, ACM, , p. 387–394 (ISBN 0897913612, DOI 10.1145/100216.100269, lire en ligne, consulté le )
- (en) Boaz Barak, Public Key Cryptography, Lecture 14, Princeton University, (lire en ligne)
- (en) R. Impagliazzo et S. Rudich, « Limits on the provable consequences of one-way permutations », STOC '89 Proceedings of the twenty-first annual ACM symposium on Theory of computing, ACM, , p. 44–61 (ISBN 0897913078, DOI 10.1145/73007.73012, lire en ligne, consulté le )
- (en) Y. Gertner, T. Malkin et O. Reingold, « On the impossibility of basing trapdoor functions on trapdoor predicates », Proceedings 2001 IEEE International Conference on Cluster Computing, , p. 126–135 (DOI 10.1109/SFCS.2001.959887, lire en ligne, consulté le )
- (en) Oded Goldreich, Shafi Goldwasser et Shai Halevi, « Public-key cryptosystems from lattice reduction problems », dans Advances in Cryptology — CRYPTO '97, Springer Berlin Heidelberg, (ISBN 9783540633846, DOI 10.1007/bfb0052231, lire en ligne), p. 112–131
- (en) Craig Gentry, Chris Peikert et Vinod Vaikuntanathan, « Trapdoors for hard lattices and new cryptographic constructions », STOC '08 Proceedings of the fortieth annual ACM symposium on Theory of computing, ACM, , p. 197–206 (ISBN 9781605580470, DOI 10.1145/1374376.1374407, lire en ligne, consulté le )
- (en) David Cash, Dennis Hofheinz, Eike Kiltz et Chris Peikert, « Bonsai Trees, or How to Delegate a Lattice Basis », Journal of Cryptology, vol. 25, no 4, , p. 601–639 (ISSN 0933-2790 et 1432-1378, DOI 10.1007/s00145-011-9105-2, lire en ligne, consulté le )
- (en) Daniele Micciancio et Chris Peikert, « Trapdoors for Lattices: Simpler, Tighter, Faster, Smaller », dans Advances in Cryptology – EUROCRYPT 2012, Springer Berlin Heidelberg, (ISBN 9783642290107, DOI 10.1007/978-3-642-29011-4_41, lire en ligne), p. 700–718
- (en) Dan Boneh et Victor Shoup, « A Graduate Course in Applied Cryptography », sur crypto.stanford.edu (consulté le )










![{\displaystyle \Pr _{(f,f^{-1})\gets G,x\gets U(f)}\left[A\left(1^{\lambda },f,f(x)\right)=x\right]<\epsilon (\lambda )}](https://img.franco.wiki/i/c0618aa0be235a8a726b090ec5c584cfcc5e9981.svg)




