Facteur d'intensité des contraintes

Le facteur d'intensité des contraintes[note 1], généralement noté $K$ , est utilisé en mécanique de la rupture pour décrire l'état des contraintes à l'extrémité d'une fissure[1]. Ce concept est généralement utilisé avec l'hypothèse que le matériau est homogène, et dans un régime élastique linéaire isotrope. Il est notamment utilisé en tolérance aux dommages pour fournir des critères de rupture. Le facteur d'intensité des contraintes peut également être étendu aux matériaux qui présentent une plasticité confinée en pointe de fissure.

Coordonnées polaires en pointe de fissure.

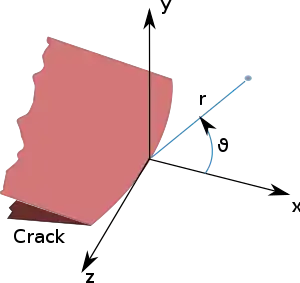
La valeur de $K$ dépend de la géométrie de l'éprouvette, de la taille et de la position de la fissure (ou de l'entaille), et est proportionnelle au niveau de chargement (charge appliquée et contraintes résiduelles)[1]. Dans sa formulation générique, le facteur d'intensité des contraintes s'écrit[2] - [3] :

K=\sigma {\sqrt {\pi a}}\,f(a/W)

où $\sigma$ est la contrainte appliquée, et où $f(a/W)$ (parfois noté Y ou $\beta$ ) est fonction de la géométrie de l'éprouvette, et du ratio entre la longueur de fissure, $a$ , et la largeur de l'échantillon, $W$ .

En élasticité linéaire, la distribution des contraintes $\sigma _{ij}$ à proximité de la pointe de fissure s'exprime en coordonnées polaires[note 2] sous la forme[4] :

\sigma _{ij}(r,\theta )={\frac {K}{\sqrt {2\pi r}}}\,f_{ij}(\theta )+O(1)

où $K$ est le facteur d'intensité des contraintes (habituellement exprimé en MPa√m) et $f_{ij}$ est une quantité sans dimension qui varie avec la géométrie. Théoriquement, quand $r$ tend vers 0, la contrainte $\sigma _{ij}$ tend vers $\infty$ , ce qui créerait une singularité de contrainte[5]. En pratique, cette singularité n'est pas obtenue, car de la plasticité apparaît dès que la contrainte dépasse la limite d'élasticité du matériau. Si la zone plastique en pointe de fissure est petite par rapport à la longueur de la fissure, la formule reste applicable asymptotiquement.

Le facteur d'intensité des contraintes ne doit pas être confondu avec la notion de concentration de contrainte.

Facteurs d'intensité des contraintes en modes I, II et III

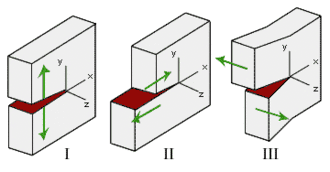
Représentation des modes de chargement I, II et III.

En 1957, George Irwin a découvert que les contraintes autour d'une fissure pouvaient être exprimées proportionnellement à un paramètre appelé facteur d'intensité des contraintes. Il a également noté qu'une fissure soumise à un chargement quelconque pouvait être décomposée en trois types de modes de fissuration linéairement indépendants[6], appelés « mode I », « mode II » et « mode III ». Le mode I est un mode d'ouverture (traction) où les surfaces de la fissure s'écartent. Le mode II est un mode de glissement (cisaillement dans le plan) où les surfaces opposées de la fissure glissent l'une sur l'autre dans une direction perpendiculaire au front de fissure. Le mode III est un mode de déchirement (cisaillement antiplan) où les surfaces opposées de la fissure se déplacent l'une par rapport à l'autre parallèlement au front de fissure. Le mode I est le type de chargement le plus couramment rencontré.

Le facteur d'intensité des contraintes pour les modes I, II et III sont désignés respectivement $K_{\rm {I}}$ , $K_{\rm {II}}$ et $K_{\rm {III}}$ . Ces facteurs sont formellement définis par les formules suivantes[7] :

{\begin{aligned}K_{\rm {I}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yy}(r,0)\\K_{\rm {II}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yx}(r,0)\\K_{\rm {III}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yz}(r,0)\,.\end{aligned}}

Équations des champs de contrainte et de déplacement

En mode I, le champ de contraintes exprimé en fonction de $K_{\rm {I}}$ s'écrit[6] :

\left\{{\begin{aligned}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{aligned}}\right\}={\frac {K_{\rm {I}}}{\sqrt {2\pi r}}}\cos {\frac {\theta }{2}}\left\{{\begin{aligned}1-\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\1+\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\\sin {\frac {\theta }{2}}\cos {\frac {3\theta }{2}}\end{aligned}}\right\}

et en coordonnées polaires :

\left\{{\begin{aligned}\sigma _{rr}\\\sigma _{\theta \theta }\\\sigma _{r\theta }\end{aligned}}\right\}={\frac {K_{\rm {I}}}{\sqrt {2\pi r}}}\cos {\frac {\theta }{2}}\left\{{\begin{aligned}1+\sin ^{2}{\frac {\theta }{2}}\\\cos ^{2}{\frac {\theta }{2}}\\\sin {\frac {\theta }{2}}\cos {\frac {\theta }{2}}\end{aligned}}\right\}

\sigma _{zz}=\nu _{1}(\sigma _{xx}+\sigma _{yy})=\nu _{1}(\sigma _{rr}+\sigma _{\theta \theta })

\sigma _{xz}=\sigma _{yz}=\sigma _{rz}=\sigma _{\theta z}=0

Les déplacements s'écrivent :

\left\{{\begin{aligned}u_{x}\\u_{y}\end{aligned}}\right\}={\frac {K_{\rm {I}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[(2\kappa +1)\sin {\frac {\theta }{2}}-\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}

\left\{{\begin{aligned}u_{r}\\u_{\theta }\end{aligned}}\right\}={\frac {K_{\rm {I}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}

u_{z}=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{xx}+\sigma _{yy})=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{rr}+\sigma _{\theta \theta })

où, en conditions de contraintes planes

\kappa ={\frac {(3-\nu )}{(1+\nu )}}

\nu _{1}=0

\nu _{2}=\nu

et en déformations planes

\kappa =(3-4\nu )

\nu _{1}=\nu

\nu _{2}=0

La composante du mode II s'écrit :

\left\{{\begin{aligned}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{aligned}}\right\}={\frac {K_{\rm {II}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}-\sin {\frac {\theta }{2}}(2+\cos {\frac {\theta }{2}}\cos {\frac {3\theta }{2}})\\\sin {\frac {\theta }{2}}\cos {\frac {\theta }{2}}\cos {\frac {3\theta }{2}}\\\cos {\frac {\theta }{2}}(1-\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}})\end{aligned}}\right\}

\left\{{\begin{aligned}\sigma _{rr}\\\sigma _{\theta \theta }\\\sigma _{r\theta }\end{aligned}}\right\}={\frac {K_{\rm {II}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}\sin {\frac {\theta }{2}}(1-3\sin ^{2}{\frac {\theta }{2}})\\-3\sin {\frac {\theta }{2}}\cos ^{2}{\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}(1-3\sin ^{2}{\frac {\theta }{2}})\end{aligned}}\right\}

\sigma _{zz}=\nu _{1}(\sigma _{xx}+\sigma _{yy})=\nu _{1}(\sigma _{rr}+\sigma _{\theta \theta })

\sigma _{xz}=\sigma _{yz}=\sigma _{rz}=\sigma _{\theta z}=0

\left\{{\begin{aligned}u_{x}\\u_{y}\end{aligned}}\right\}={\frac {K_{\rm {II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa +3)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\\-(1+\nu )\left[(2\kappa -3)\cos {\frac {\theta }{2}}+\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}

\left\{{\begin{aligned}u_{r}\\u_{\theta }\end{aligned}}\right\}={\frac {K_{\rm {II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[-(2\kappa -1)\sin {\frac {\theta }{2}}+3\sin {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\cos {\frac {\theta }{2}}+3\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}

u_{z}=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{xx}+\sigma _{yy})=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{rr}+\sigma _{\theta \theta })

La composante du mode III donne

\left\{{\begin{aligned}\sigma _{xz}\\\sigma _{yz}\end{aligned}}\right\}={\frac {K_{\rm {III}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}-\sin {\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}\end{aligned}}\right\}

\left\{{\begin{aligned}\sigma _{rz}\\\sigma _{\theta z}\end{aligned}}\right\}={\frac {K_{\rm {III}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}\sin {\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}\end{aligned}}\right\}

avec $\sigma _{xx}=\sigma _{yy}=\sigma _{rr}=\sigma _{\theta \theta }=\sigma _{zz}=\sigma _{xy}=\sigma _{r\theta }=0$ .

u_{z}={\frac {2K_{\rm {III}}}{E}}{\sqrt {\frac {r}{2\pi }}}\left\{2(1+\nu )\sin {\frac {\theta }{2}}\right\}

u_{x}=u_{y}=u_{r}=u_{\theta }=0

Taux de restitution d'énergie (G) et intégrale J

En contraintes planes, le taux de restitution d'énergie ( $G$ ) d'une fissure chargée en mode I pur, ou en mode II pur est relié au facteur d'intensité des contraintes par[8] :

G_{\rm {I}}=K_{\rm {I}}^{2}\left({\frac {1}{E}}\right)

G_{\rm {II}}=K_{\rm {II}}^{2}\left({\frac {1}{E}}\right)

où $E$ est le module de Young et $\nu$ est le coefficient de Poisson du matériau. Cette relation suppose que le matériau est homogène, a un comportement élastique linéaire isotrope, et que la fissure propage dans la direction de la fissure initiale.

En déformations planes, la relation est légèrement différente[8] :

G_{\rm {I}}=K_{\rm {I}}^{2}\left({\frac {1-\nu ^{2}}{E}}\right)\,

G_{\rm {II}}=K_{\rm {II}}^{2}\left({\frac {1-\nu ^{2}}{E}}\right)\,.

Pour un chargement en mode III pur,

G_{\rm {III}}=K_{\rm {III}}^{2}\left({\frac {1}{2\mu }}\right)=K_{\rm {III}}^{2}\left({\frac {1+\nu }{E}}\right)

où $\mu$ est le module de cisaillement.

En contraintes planes comme en déformations planes, le taux de restitution d'énergie total est la combinaison linéaire des trois contributions[8] :

G=G_{\rm {I}}+G_{\rm {II}}+G_{\rm {III}}\,.

En élasticité linéaire, les relations ci-dessus peuvent également être utilisées pour relier l'intégrale J au facteur d'intensité des contraintes, car on a alors :

G=J=\int _{\Gamma }\left(W~dx_{2}-\mathbf {t} \cdot {\cfrac {\partial \mathbf {u} }{\partial x_{1}}}~ds\right)\,.

Ténacité

On appelle communément « ténacité » le facteur d'intensité des contraintes critique au-delà duquel la rupture se produit. Les valeurs de ténacité peuvent être déterminées expérimentalement à l'aide d'éprouvettes préfissurées.

En mode I, pour le cas des déformations planes, la ténacité se note $K_{\mathrm {Ic} }$ (généralement exprimée en MPa√m). Le $K_{\mathrm {Ic} }$ est un paramètre qui peut être utilisé en conception lorsque la tolérance aux dommages fait partie du cahier des charges (ponts, bâtiments, aéronautique, etc.).

La notion se généralise (« critère en G ») en reliant la ténacité aux facteurs d'intensité des contraintes pour les trois modes :

K_{\rm {c}}^{2}=K_{\rm {I}}^{2}+K_{\rm {II}}^{2}+{\frac {E'}{2\mu }}\,K_{\rm {III}}^{2}

où $K_{\rm {c}}$ est la ténacité, $E'=E/(1-\nu ^{2})$ en déformations planes et $E'=E$ en contraintes planes. La notation $K_{\rm {c}}$ est souvent utilisée pour décrire le facteur d'intensité des contraintes critique en contraintes planes.

Exemples

Plaque infinie

Dans une plaque dont l'épaisseur et la longueur de fissure sont très petits devant la largeur et la hauteur, il est possible de calculer les facteurs d'intensité des contraintes en faisant l'hypothèse d'une plaque infinie.

Différentes formules peuvent être utilisées suivant que l'application de la force est uniaxiale ou biaxiale, ponctuelle ou uniforme, perpendiculaire ou oblique par rapport à la fissure.

Plaque infinie : contrainte uniaxiale uniforme
Le facteur d'intensité des contraintes pour une fissure rectiligne de longueur $2a$ perpendiculaire à la direction de chargement, insérée dans un plan infini, ayant un champ de contrainte uniforme 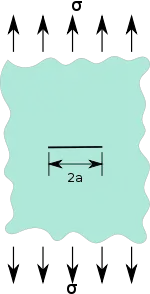$\sigma$ est [5] - [7] : $K_{\mathrm {I} }=\sigma {\sqrt {\pi a}}$	Fissure dans une plaque infinie sous un chargement en mode I.

Plaque infinie : fissure oblique dans un champ de contraintes biaxial

Pour une fissure oblique de longueur

2a

dans un champ de contrainte biaxial, avec une contrainte

\sigma

dans la direction

y

\alpha \sigma

dans la direction

x

, les facteurs d'intensité des contraintes sont [7] :

{\begin{aligned}K_{\rm {I}}&=\sigma {\sqrt {\pi a}}\left(\cos ^{2}\beta +\alpha \sin ^{2}\beta \right)\\K_{\rm {II}}&=\sigma {\sqrt {\pi a}}\left(1-\alpha \right)\sin \beta \cos \beta \end{aligned}}

où $\beta$ est l'angle que fait la fissure avec la direction $x$ .

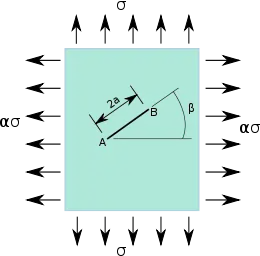Une fissure oblique dans une plaque mince sous chargement biaxial.

Plaque infinie : fissure dans une plaque soumise à une force ponctuelle dans le plan

Considérons une plaque de dimensions

2h\times 2b

contenant une fissure de longueur

2a

, à laquelle une force ponctuelle de composantes

F_{x}

F_{y}

est appliquée au point (

x,y

Dans le cas où la plaque est grande par rapport à la taille de la fissure et l'emplacement de la force est relativement proche de la fissure, c'est-à-dire, $h\gg a$ , $b\gg a$ , $x\ll b$ , $y\ll h$ , la plaque peut être considérée comme infinie. Dans ce cas, les facteurs d'intensité des contraintes pour $F_{x}$ en pointe de fissure B ( $x=a$ ) sont :

{\begin{aligned}K_{\rm {I}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}+{\frac {1}{\kappa -1}}H_{1}\right]\\K_{\rm {II}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left[G_{2}+{\frac {1}{\kappa +1}}H_{2}\right]\end{aligned}}

où

{\begin{aligned}G_{1}&=1-{\text{Re}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\,,\,\,G_{2}=-{\text{Im}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\\H_{1}&={\text{Re}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\,,\,\,H_{2}=-{\text{Im}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\end{aligned}}

avec $z=x+iy$ , ${\bar {z}}=x-iy$ , $\kappa =3-4\nu$ en déformations planes, $\kappa =(3-\nu )/(1+\nu )$ en contraintes planes, et $\nu$ est le coefficient de Poisson. Les facteurs d'intensité des contraintes pour $F_{y}$ à la pointe B sont

{\begin{aligned}K_{\rm {I}}&={\frac {F_{y}}{2{\sqrt {\pi a}}}}\left[G_{2}-{\frac {1}{\kappa +1}}H_{2}\right]\\K_{\rm {II}}&=-{\frac {F_{y}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}-{\frac {1}{\kappa -1}}H_{1}\right]\,.\end{aligned}}

Les facteurs d'intensité des contraintes à la pointe A ( $x=-a$ ) peuvent être déterminés à partir des relations ci-dessus. Pour la charge $F_{x}$ à l'emplacement $(x,y)$ ,

K_{\rm {I}}(-a;x,y)=-K_{\rm {I}}(a;-x,y)\,,\,\,K_{\rm {II}}(-a;x,y)=K_{\rm {II}}(a;-x,y)\,.

De même pour la charge $F_{y}$ ,

K_{\rm {I}}(-a;x,y)=K_{\rm {I}}(a;-x,y)\,,\,\,K_{\rm {II}}(-a;x,y)=-K_{\rm {II}}(a;-x,y)\,.

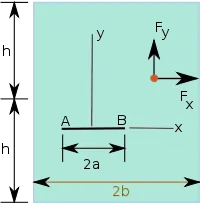Une fissure dans une plaque sous l'action d'une force ponctuelle de composantes

F_{x}

F_{y}

Plaque infinie : force appliquée sur la fissure

Si la fissure est chargée par une force ponctuelle

F_{y}

située à

y=0

-a<x<a

, les facteurs d'intensité des contraintes au point B sont[7] :

K_{\rm {I}}={\frac {F_{y}}{2{\sqrt {\pi a}}}}{\sqrt {\frac {a+x}{a-x}}}\,,\,\,K_{\rm {II}}=-{\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\,.

Si la force est répartie uniformément entre $-a<x<a$ , alors le facteur d'intensité des contraintes à la pointe B est

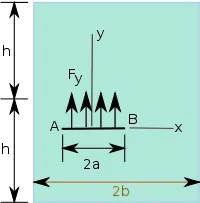K_{\rm {I}}={\frac {1}{2{\sqrt {\pi a}}}}\int _{-a}^{a}F_{y}(x)\,{\sqrt {\frac {a+x}{a-x}}}\,{\rm {d}}x\,,\,\,K_{\rm {II}}=-{\frac {1}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\int _{-a}^{a}F_{y}(x)\,{\rm {d}}x,\,.

Une fissure chargée dans une plaque.

Plaque finie

Dans les cas où l'hypothèse d'une plaque infinie n'est pas applicable, il est nécessaire de recourir à d'autres formules, qui sont généralement plus complexes, et qui dépendent de la position de la fissure (centrale, débouchante, décalée, etc.).

Plaque finie : contrainte uniaxiale uniforme

Si la fissure est située au centre d'une plaque finie de largeur

2b

et de hauteur

2h

, le facteur d'intensité des contraintes peut être approché par la formule[7] :

K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\cfrac {1-{\frac {a}{2b}}+0.326\left({\frac {a}{b}}\right)^{2}}{\sqrt {1-{\frac {a}{b}}}}}\right]\,.

Si la fissure n'est pas située au centre de la largeur, c'est-à-dire, $d\neq b$ , le facteur d'intensité des contraintes à l'emplacement A peut être approximé par le développement en série[7] - [9] :

K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\left[1+\sum _{n=2}^{M}C_{n}\left({\frac {a}{b}}\right)^{n}\right]

où les facteurs $C_{n}$ peuvent être trouvés à partir des ajustements aux courbes d'intensité de contrainte [7]^:6 pour différentes valeurs de $d$ . Une expression similaire (mais pas identique) peut être trouvée pour la pointe B de la fissure. Des expressions alternatives pour les facteurs d'intensité de contrainte en A et B sont [10]

K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\,\Phi _{A}\,\,,K_{\rm {IB}}=\sigma {\sqrt {\pi a}}\,\Phi _{B}

où

{\begin{aligned}\Phi _{A}&:=\left[\beta +\left({\frac {1-\beta }{4}}\right)\left(1+{\frac {1}{4{\sqrt {\sec \alpha _{A}}}}}\right)^{2}\right]{\sqrt {\sec \alpha _{A}}}\\\Phi _{B}&:=1+\left[{\frac {{\sqrt {\sec \alpha _{AB}}}-1}{1+0.21\sin \left\{8\,\tan ^{-1}\left[\left({\frac {\alpha _{A}-\alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)^{0.9}\right]\right\}}}\right]\end{aligned}}

avec

{\displaystyle \beta

Dans les expressions ci-dessus $d$ est la distance entre le centre de la fissure et la limite la plus proche du point A. Notez que lorsque $d=b$ les expressions ci-dessus ne se simplifient pas en l'expression approchée d'une fissure centrée.

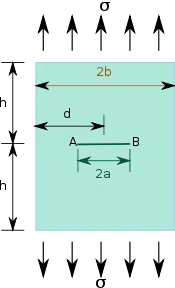Fissure dans une plaque finie soumise à un chargement en mode I.

Plaque finie : fissure débouchante sous chargement unixial

Pour une plaque de dimensions

2h\times b

contenant une fissure débouchante de longueur

a

, si les dimensions de la plaque sont telles que

h/b\geq 0.5

a/b\leq 0.6

, le facteur d'intensité des contraintes en pointe de fissure sous un chargement uniaxial

\sigma

est[5] :

K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[1.122-0.231\left({\frac {a}{b}}\right)+10.55\left({\frac {a}{b}}\right)^{2}-21.71\left({\frac {a}{b}}\right)^{3}+30.382\left({\frac {a}{b}}\right)^{4}\right]\,.

Dans le cas où $h/b\geq 1$ et $a/b\geq 0.3$ , le facteur d'intensité des contraintes peut être approximé par

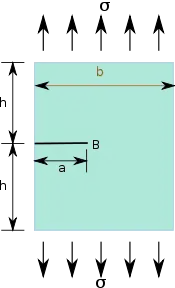K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\frac {1+3{\frac {a}{b}}}{2{\sqrt {\pi {\frac {a}{b}}}}\left(1-{\frac {a}{b}}\right)^{3/2}}}\right]\,.

Fissure débouchante dans une plaque finie sous chargement uniaxial.

Volume infini

Le cas du volume infinie est l'équivalent en trois dimensions de la plaque infinie. Elle correspond à des cas où une fissure amorce sur un défaut à l'intérieur d'un matériau.

Volume infini : fissure circulaire
Le facteur d'intensité des contraintes en pointe d'une fissure circulaire de rayon $a$ dans un volume infini sous chargement uniaxial 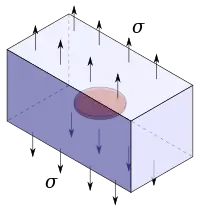$\sigma$ est[1] : $K_{\rm {I}}={\frac {2}{\pi }}\sigma {\sqrt {\pi a}}\,.$	Fissure circulaire dans un volume infini sous chargement uniaxial.

Éprouvettes

Plusieurs éprouvettes normalisées existent pour caractériser la ténacité des matériaux. Des formules tabulées de facteurs d'intensité des contraintes ont été développées pour faciliter le dépouillement des résultats d'essais. L'éprouvette C(T) est l'une des éprouvettes de ténacité les plus répandues.

Éprouvette : C(T)

Le facteur d'intensité des contraintes en pointe de fissure d'une éprouvette C(T) est [11] :

{\begin{aligned}K_{\rm {I}}&={\frac {P}{B}}{\sqrt {\frac {\pi }{W}}}\left[16.7\left({\frac {a}{W}}\right)^{1/2}-104.7\left({\frac {a}{W}}\right)^{3/2}+369.9\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-573.8\left({\frac {a}{W}}\right)^{7/2}+360.5\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}

où $P$ est la charge appliquée, $B$ est l'épaisseur de l'éprouvette, $a$ est la longueur de fissure, et $W$ est la distance entre l'axe des trous et le bord opposé.

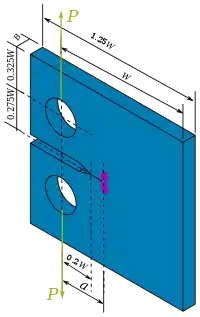Éprouvette C(T), pouvant être utilisée pour les essais de ténacité.

Éprouvette : flexion trois points (SENB)

Le facteur d'intensité des contraintes en pointe de fissure d'une éprouvette de flexion trois points (en anglais Single edge notch bending - SENB) est[11] :

{\begin{aligned}K_{\rm {I}}&={\frac {4P}{B}}{\sqrt {\frac {\pi }{W}}}\left[1.6\left({\frac {a}{W}}\right)^{1/2}-2.6\left({\frac {a}{W}}\right)^{3/2}+12.3\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-21.2\left({\frac {a}{W}}\right)^{7/2}+21.8\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}

où $P$ est la charge appliquée, $B$ est l'épaisseur de l'éprouvette, $a$ est la longueur de fissure, et $W$ est la largeur de l'échantillon.

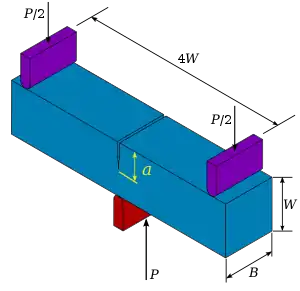Éprouvette de flexion trois points (SENB).

Voir aussi

Notes et références

Notes

Les formes au singulier facteur d'intensité de contrainte ou facteur d'intensité de contraintes sont également utilisées dans la littérature franophone.
L'origine des coordonnées polaires ( $r,\theta$ ) est prise au niveau du front de fissure.

Références

T. L. Anderson, Fracture mechanics: fundamentals and applications, CRC Press, 2005
W. O. Soboyejo, Mechanical properties of engineered materials, Marcel Dekker, 2003 (ISBN 0-8247-8900-8, OCLC 300921090, lire en ligne), « 11.6.2 Crack Driving Force and Concept of Similitude »
M. (Michael) Janssen, Fracture mechanics, London, 2nd, 2004, 41 p. (ISBN 0-203-59686-2, OCLC 57491375, lire en ligne)
Hiroshi Tada, P. C. Paris et George R. Irwin, The Stress Analysis of Cracks Handbook, 3rd, février 2000
Liu et al., « An improved semi-analytical solution for stress at round-tip notches », Engineering Fracture Mechanics, vol. 149,‎ 2015, p. 134–143 (lire en ligne)
S. Suresh, Fatigue of Materials, Cambridge University Press, 2004 (ISBN 978-0-521-57046-6)
D. P. Rooke et D. J. Cartwright, Compendium of stress intensity factors, HMSO Ministry of Defence. Procurement Executive, 1976
Ecole des mines de Paris, « Mécanique de la rupture », sur mms2.ensmp.fr (consulté le 27 novembre 2021)
Isida, M., 1966, Stress intensity factors for the tension of an eccentrically cracked strip, Transactions of the ASME Applied Mechanics Section, v. 88, p.94.
K. Kathiresan, T. R. Brussat et T. M. Hsu, Advanced life analysis methods. Crack Growth Analysis Methods for Attachment Lugs, p.175, Flight Dynamics Laboratory, Air Force Wright Aeronautical Laboratories, AFSC W-P Air Force Base, Ohio (n^o AFWAL-TR-84-3080), 1984
Bower, A. F., Applied mechanics of solids, CRC Press., 2009

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Stress intensity factor » (voir la liste des auteurs).

Liens externes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.