Epsilon algorithme

En analyse numérique, l'ε-algorithme est un algorithme non linéaire d'accélération de la convergence de suites numériques. Cet algorithme a été proposé par Peter Wynn[1] en 1956 pour calculer la transformation de Shanks. C'est l'un des algorithmes d'accélération de la convergence les mieux connus et les plus utilisés. C'est une généralisation de l'algorithme Delta-2 d'Aitken.

Présentation

Soit une suite numérique $S n$ dont on cherche à connaitre la limite $S$ . l'ε-algorithme consiste à calculer un tableau en initialisant la première colonne par la suite $S n$ , et en calculant les autres cases à l'aide des relations suivantes :

\forall n,\quad \varepsilon _{-1}^{(n)}=0\quad ,\quad \varepsilon _{2n}^{(-n-1)}=0\quad ,\quad \varepsilon _{0}^{(n)}=S_{n}.

\forall n,k,\quad \varepsilon _{k+1}^{(n)}=\varepsilon _{k-1}^{(n+1)}+{\frac {1}{\varepsilon _{k}^{(n+1)}-\varepsilon _{k}^{(n)}}}.

Les différentes colonnes d'indice $k$ pair du tableau fournissent d'autres suites convergeant en général plus vite que la suite $S n$ d'origine. Les colonnes d'indice impair peuvent être considérées comme des intermédiaires de calcul.

On présente traditionnellement les résultats de l'ε-algorithme sous forme d'un tableau aux lignes décalées : la formule de calcul de l'ε-algorithme relie ainsi les termes formant un losange dans le tableau.

{\begin{matrix}0&&0&&0&\cdots \\&\varepsilon _{0}^{(0)}=S_{0}&&\varepsilon _{2}^{(-1)}&&\varepsilon _{4}^{(-2)}\cdots \\0&&\varepsilon _{1}^{(0)}&&\varepsilon _{3}^{(-1)}&\cdots \\&\varepsilon _{0}^{(1)}=S_{1}&&\varepsilon _{2}^{(0)}&&\varepsilon _{4}^{(-1)}\cdots \\0&&\varepsilon _{1}^{(1)}&&\varepsilon _{3}^{(0)}&\cdots \\&\varepsilon _{0}^{(2)}=S_{2}&&\varepsilon _{2}^{(1)}&&\varepsilon _{4}^{(0)}\cdots \\0&&\varepsilon _{1}^{(2)}&&\varepsilon _{3}^{(1)}&\cdots \\&\varepsilon _{0}^{(3)}=S_{3}&&\varepsilon _{2}^{(2)}&&\varepsilon _{4}^{(1)}\cdots \\&\vdots &&\vdots &&\vdots \\\end{matrix}}

Propriétés

Le tableau obtenu par l'ε-algorithme est une des méthodes utilisées pour calculer la transformée de Shanks d'une suite. En effet :

\forall k,n,\quad e_{k}(S_{n})=\varepsilon _{2k}^{(n)}.

où $e k (S n)$ est la transformée de Shanks d'ordre $k$ de la suite $S n$ . L'ε-algorithme partage donc toutes les propriétés de la transformée de Shanks. Notamment, l'ε-algorithme est un moyen pour calculer la table de Padé d'une série entière. De même, la suite $ε (n) 2$ correspond au Delta-2 d'Aitken. Les approximants de Padé à plusieurs variables peuvent aussi très simplement être calculés à l'aide de l'ε-algorithme. Par exemple, pour une fonction à deux variables, dont le développement de Taylor est :

f(x,y)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }a_{i,j}.x^{i}.y^{j}

Sa table de Padé peut être obtenue à l'aide de l'ε-algorithme, en initialisant la première colonne par :

\varepsilon _{0}^{(n)}=\sum _{m=0}^{n}\left(\sum _{i+j=m}a_{i,j}.x^{i}.y^{j}\right)

Variantes

ε-algorithme vectoriel

Il existe plusieurs variantes de l'ε-algorithme pouvant être utilisées avec des suites vectorielles (ε-algorithme vectoriel, topologique ou scalaire appliqué à chacune des composantes du vecteur). L'ε-algorithme vectoriel est analogue dans sa forme à l'ε-algorithme classique :

\forall n,\quad \varepsilon _{-1}^{(n)}=0,\quad \varepsilon _{2n}^{(-n-1)}=0,\quad \varepsilon _{0}^{(n)}=S_{n}.

\forall n,k,\quad \varepsilon _{k+1}^{(n)}=\varepsilon _{k-1}^{(n+1)}+{(\varepsilon _{k}^{(n+1)}-\varepsilon _{k}^{(n)})}^{-1}.

où les suites $S n$ et les 0 sont des vecteurs.

Reste à définir ce qu'est l'« inverse » d'un vecteur. On pourra prendre par exemple comme inverse d'un vecteur $U$ :

U^{-1}={\frac {U}{{\|U\|}^{2}}}

où la norme du vecteur est la norme euclidienne. L'ε-algorithme vectoriel a de nombreuses applications pratiques mais est très sensible aux erreurs d'arrondi. Il permet notamment de généraliser la méthode de Aitken-Steffensen à des systèmes d'équations non linéaires. Il fournissant ainsi un algorithme à convergence quadratique ne nécessitant pas de calcul du jacobien, à l'inverse de la méthode de Newton.

L'ε-algorithme matriciel existe pour les matrices carrées, dans ce cas l'inverse apparaissant dans l'algorithme est tout simplement celui d'une matrice carrée classique.

ε-algorithme confluent

L'ε-algorithme classique accélère une suite numérique, c'est-à-dire une fonction d'une variable discrète $n$ . La version confluente de cet algorithme accélère la convergence d'une fonction d'une variable continue $t$ . On l'obtient en faisant un changement de variable $x = t + nh$ à l'algorithme d'origine, et en faisant tendre $h$ vers 0. on obtient :

\varepsilon _{-1}(t)=0,\qquad \varepsilon _{0}(t)=f(t)

\varepsilon _{k+1}(t)=\varepsilon _{k-1}(t)+{\frac {1}{\varepsilon '_{k}(t)}},\quad k=0,1,...

Cet algorithme est utilisé par exemple pour l'évaluation des intégrales impropres lorsque les dérivées de la fonction sont accessibles, ou à l'élaboration de séries asymptotiques pour certaines fonctions.

La dérivée des termes apparaissant dans la formule peuvent se ramener aux dérivées de la fonction de base $f (t)$ par calcul formel, où en utilisant les relations des déterminants de Henkel :

\varepsilon '_{2k}(t)={\frac {H_{k}^{(1)}H_{k+1}^{(1)}}{(H_{k}^{(2)})^{2}}}

\varepsilon '_{2k+1}(t)=-{\frac {H_{k}^{(2)}H_{k+1}^{(2)}}{(H_{k+1}^{(1)})^{2}}}

avec

\forall n,k\in \mathbb {N} ,H_{k+2}^{(n-1)}H_{k}^{(n+1)}+(H_{k+1}^{(n)})^{2}=H_{k+1}^{(n-1)}H_{k+1}^{(n+1)},

\forall n\in \mathbb {N} ,\,H_{0}^{(n)}=1{\text{   }}H_{1}^{(n)}=f^{(n)}(t).

On trouve, en explicitant les premières expressions :

{\frac {1}{\varepsilon '_{1}(t)}}=-{\frac {[f'(t)]^{2}}{f''(t)}}

{\frac {1}{\varepsilon '_{2}(t)}}=-{\frac {f'(t)f'''(t)-f''^{2}(t)}{f''(t)[f''(t)f^{(4)}(t)-f'''^{2}(t))]^{2}}}

ε-algorithme dépendant d'une suite auxiliaire

Il arrive fréquemment que la suite à accélérer $S n$ dépende d'une suite auxiliaire $x n$ , celle-ci tendant vers l'infini (par exemple des approximations par discrétisation avec un maillage de plus en plus fin). Il est possible d'utiliser l'ε-algorithme de base dans ces cas mais la façon dont évolue la suite $x n$ associée (par exemple l'évolution du nombre de mailles entre chaque $S n$ ) est un renseignement précieux qui pourrait aider l'accélération de la convergence. Deux variantes de l'ε-algorithme utilisent cette information supplémentaire et donnent souvent de meilleurs résultats.

\forall n,\quad \varepsilon _{-1}^{(n)}=0,\quad \varepsilon _{2n}^{(-n-1)}=0,\quad \varepsilon _{0}^{(n)}=S_{n}.

\varepsilon _{k+1}^{(n)}=\varepsilon _{k-1}^{(n+1)}+{\frac {x_{n+1}-x_{n}}{\varepsilon _{k}^{(n+1)}-\varepsilon _{k}^{(n)}}}.

Et la deuxième variante :

\forall n,\quad \varepsilon _{-1}^{(n)}=0,\quad \varepsilon _{2n}^{(-n-1)}=0,\quad \varepsilon _{0}^{(n)}=S_{n}.

\forall n,k,\quad \varepsilon _{k+1}^{(n)}=\varepsilon _{k-1}^{(n+1)}+{\frac {x_{n+k+1}-x_{n+k}}{\varepsilon _{k}^{(n+1)}-\varepsilon _{k}^{(n)}}}.

Ces algorithmes s'apparentent aux méthodes par extrapolation (extrapolation de Richardson ou ρ-algorithme). Ils peuvent accélérer des suites à convergence logarithmique, que l'ε-algorithme classique n'accélère pas.

ε-algorithme d'interpolation

L'ε-algorithme classique permet de calculer la table de Padé d'une fonction lorsque les termes de la suite $S n$ sont les sommes partielles du développement limité de cette fonction. Un variante[2] permet de construire la table des fractions rationnelles d'interpolation d'une fonction en partant de la suite des polynômes d'interpolation.

\forall n,\quad \varepsilon _{-1}^{(n)}=0,\quad \varepsilon _{2n}^{(-n-1)}=0,\quad \varepsilon _{0}^{(n)}=P_{n}(x),

\forall k,n\ \varepsilon _{k+1}^{(n)}=\varepsilon _{k-1}^{(n+1)}+{\frac {1}{(x-x_{n+k+1})\cdot (\varepsilon _{k}^{(n+1)}-\varepsilon _{k}^{(n)})}},

\forall k,n\ R_{n,k}(x)=\varepsilon _{2k}^{(n-k)}.

Le polynôme $P n (x)$ étant la valeur en x du polynôme d'interpolation passant par les points $(x 0, y 0) , (x 1, y 1),...,(x n, y n)$ , que l'on pourra calculer par la méthode de Lagrange, de Newton où de Neville, par exemple. $R n, k (x)$ est la fraction rationnelle de degré $n$ au numérateur et $k$ au dénominateur passant par les points $(x 0, y 0) , (x 1, y 1),...,(x n + k, y n + k)$ .

Cet algorithme peut se présenter comme un complément aux méthodes de Thiele ou Bulirsch-Stoer, avec la particularité que l'ε-algorithme permet de calculer tout le tableau des fractions rationnelles d'interpolation au lieu d'une seule diagonale, ou un escalier. De plus, si le polynôme utilisé est un polynôme d'interpolation d'Hermite (imposant d'interpoler la fonction, mais aussi sa ou ses dérivées), l'ε-algorithme d'interpolation fournira les fraction rationnelle d'interpolation vérifiant les mêmes critères que le polynôme d'Hermite. La méthode d'interpolation de Newton avec confluence des abscisses (pour les points où les dérivées sont à renseigner) est toute indiquée pour calculer le polynôme d'Hermite, d'autant que la suite des abscisses utilisée (avec les confluences) sera nécessaire pour l'ε-algorithme d'interpolation.

Règles particulières

Il peut arriver lors du calcul du tableau de l'ε-algorithme, qu'à certains endroits se produisent des divisions par 0 ou presque. Ceci peut générer des dégradations de précision pour le calcul des zones du tableau dépendant de la case suspecte, voir des plantages de programme. Plusieurs auteurs ont développé des algorithmes spéciaux[3] pour contourner les cases problématiques en cas de détection de risque de division par 0. Ces algorithmes ne fonctionnent que si les cases singulières ne sont pas trop proches les unes des autres.

Exemples

Voir aussi les exemples de la transformée de Shanks.

Accélération de la convergence d'une suite

La méthode de Bernoulli permet, sous certaines conditions, d'évaluer la plus grande (ou la plus petite) racine d'un polynôme donné. Mais la suite générée par la méthode peut converger lentement vers la valeur de la racine : l'ε-algorithme permet d'accélérer cette convergence. Par exemple, avec le polynôme $x 2 - x - 1$ dont les racines sont le nombre d'or φ et 1/φ, la suite générée par la méthode de Bernoulli donne la suite de Fibonacci $F n$ dont le ratio des termes successifs converge vers φ=1,6180339887499...

$\scriptstyle {\begin{matrix}&\varepsilon _{0}^{(n)}=F_{n+1}/F_{n}&&\varepsilon _{2}^{(n)}&&\varepsilon _{4}^{(n)}&&\varepsilon _{6}^{(n)}&&\varepsilon _{8}^{(n)}\\0\\&1\\0&&-2\\&2&&1,62500000\\0&&6&&-162\\&1,5&&1,61904761&&1,61805555\\0&&-15&&-1170&&-45090,00\\&1,66666667&&1,61818181&&1,61803278&&1,6180339985\\0&&40&&-7880&&780240,00&&-103779601,9\\&1,60000000&&1,61805555&&1,61803405&&1,6180339889&&1,61803398875\\0&&-104&&-54392&&-14196624,02&&-4926280210,4\\&1,62500000&&1,61803713&&1,61803398&&1,6180339888\\0&&273&&-371826&&253400249,03\\&1,61538461&&1,61803444&&1,61803398\\0&&-714&&-2551122\\&1,61904761&&1,61803405\\0&&1870\\&1,61764705\\\end{matrix}}$

Dans cet exemple, seuls les termes d'indice haut positif ont été calculés.

Nous constatons dans cet exemple qu'effectivement seules les colonnes paires convergent vers la suite d'origine, et ceci plus rapidement (12 chiffres exacts au lieu de 3 dans la suite initiale).

Il est à noter que l'ε-algorithme possède une propriété particulière vis-à-vis de la méthode de Bernoulli qui permet de l'utiliser aussi dans un autre but que l'accélération de la convergence : le calcul simultané de toutes les racines du polynôme au lieu d'une seule à la fois.

Soit le polynôme :

P(x)=a_{0}+a_{1}x+a_{2}x^{2}+...+a_{p}x^{p}

dont les racines $λ k$ sont réelles, telles que |λ₁|> |λ₂|>...>|λ_p|

la méthode de Bernoulli génère la suite $y n$ définie par :

\forall n,\quad y_{n+p}={\frac {-1}{a_{p}}}\left(a_{p-1}y_{n+p-1}+\ldots +a_{1}y_{n+1}+a_{0}y_{n}\right)

dont le rapport des termes consécutifs $y n +1 / y n$ converge vers λ₁.

La suite est initialisée avec $y 0$ , $y 1$ ,... $y p -1$ arbitraires, non tous nuls.

En appliquant l'ε-algorithme, non pas sur le ratio $y n +1 / y n$ , mais directement sur la suite des $y n$ , on a :

\forall k\in [\![1,p-1]\!],\quad \lim _{n\to \infty }{\frac {\varepsilon _{2k}^{(n+1)}}{\varepsilon _{2k}^{(n)}}}=\lambda _{k+1},\,\lim _{n\to \infty }{\frac {\varepsilon _{2k+1}^{(n)}}{\varepsilon _{2k+1}^{(n+1)}}}=\lambda _{k+1}.

On constate dans ce cas que les colonnes impaires s'avèrent aussi intéressantes.

La vitesse de convergence, pour $k$ fixé, est :

{\frac {\varepsilon _{2k}^{(n+1)}}{\varepsilon _{2k}^{(n)}}}=\lambda _{k+1}+O\left[\left({\frac {\lambda _{k+2}}{\lambda _{k+1}}}\right)^{n+k+1}\right]

On peut donc utiliser à nouveau l'ε-algorithme, mais cette fois pour accélérer la convergence de chacun de ces ratios, comme on l'a fait pour la suite $y n +1 / y n$ .

Résolution d'un système d'équation non linéaire

L'une des utilisations de l'ε-algorithme est de fournir une généralisation de la méthode d'Aitken-Steffensen pour des systèmes d'équations non linéaires.

La méthode consiste à réécrire le système d'équation $F (X)=0$ en un système de la forme $X = G (X)$ ( $X$ , $F$ et $G$ étant des vecteurs représentant les inconnues ou le système d'équations). En partant d'un vecteur $X 0$ arbitraire (de préférence proche de la solution du système), on génère la suite de vecteurs $X k$ de la manière suivante :

\forall k,\quad U_{0}=X_{k},

\forall n\in [\![0,2p]\!],\quad U_{n+1}=G(U_{n}).

calculer l'ε-algorithme de cette suite de vecteurs $U n$

X_{k+1}=\varepsilon _{2p}^{(0)}

avec $p$ étant le nombre d'équations du système.

La suite des $X k$ générés par cette méthode est à convergence quadratique.

Plusieurs choix pour $G$ étant possibles, il est préférable, bien que non nécessaire, de choisir $G$ de telle sorte que la suite générée $U n +1 = G (U n)$ converge vers la solution du système.

L'ε-algorithme vectoriel parait le plus adapté à cet algorithme, mais l'ε-algorithme scalaire appliqué à chacune des composantes du vecteur fonctionne aussi.

Fraction rationnelle d'interpolation

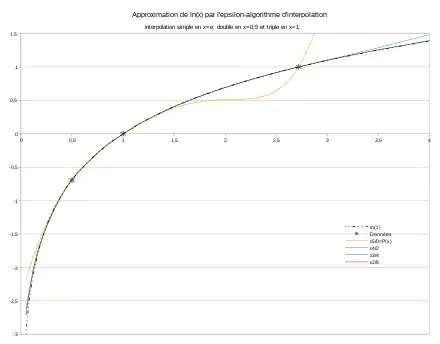
Exemple: interpolation polynomiale de la fonction logarithme népérien et calcul des fraction rationnelles correspondantes à l'aide de l'ε-algorithme d'interpolation

La fonction logarithme sera interpolée en trois points: 1/2, 1 et e. Pour tester la mise en œuvre de l'algorithme dans le cas d'une interpolation d'Hermite, l'interpolation en 1/2 sera double (interpolation du logarithme et de sa dérivée), et triple en 1 (interpolation du logarithme, et de ses dérivées premières et secondes). Il s'agit d'un polynôme de degré 5 qui doit donc vérifier :

P(0,5)=-\ln(2),P'(0,5)=2,P(1)=0,P'(1)=1,P''(1)=-1\ \mathrm {et} \ P(\mathrm {e} )=1.

Calcul des différences divisées du polynôme d'interpolation :

Tableau des différences divisées pour l'interpolation polynomiale de ln(x) en 3 points
i	x_i	y_i / d₀	d₁	d₂	d₃	d₄	d₅
0	2,71828182845904	1	0,581976706869326	-0,243279819530861	0,149405165216329	-0,178413885100506	0,24817470934455
1	1	0	1	-0,5	0,545177444479562	-0,728935333122626
2	1	0	1	-0,772588722239781	0,909645111040875
3	1	0	1,38629436111989	-1,22741127776022
4	0.5	-0,693147180559945	2
5	0.5	-0,693147180559945

Les cases en italiques correspondent à des indéterminées des différences divisées (du fait des points doubles ou triples), et sont remplacés par les valeurs de la dérivée en ce point (ou de f"(x)/2! pour la différence seconde). Les cases en gras dans le tableau sont celles utiles au calcul de la forme de Newton du polynôme d'interpolation. Le polynôme s'écrit, à l'aide de la formule de Newton :

P_{5}(x)=d_{0}+d_{1}(x-x_{0})+d_{2}(x-x_{0})(x-x_{1})+d_{3}(x-x_{0})(x-x_{1})(x-x_{2})+d_{4}(x-x_{0})(x-x_{1})(x-x_{2})(x-x_{3})+d_{5}(x-x_{0})(x-x_{1})(x-x_{2})(x-x_{3})(x-x_{4})

Calcul de P₅(2), et application de l'ε-algorithme d'interpolation.

La suite des P_i(2) servant à initialiser le tableau de l'ε-algorithme d'interpolation, est la suite de polynômes de degré 0, 1, 2... obtenue en retenant 1,2,3... termes du polynôme P₅(2) écrit sous la forme de Newton ci dessus. Cette suite de polynôme passent respectivement par les points d'abscisse (x0,y0); (x0,y0),(x1,y1); (x0,y0),(x1,y1),(x2,y2); ...

Comparaison de l'interpolation polynomiale et rationnelle par l'ε-algorithme d'interpolation

Interpolation polynomiale de ln(2)=0,693147180559945..., et calcul de l'ε-algorithme d'interpolation
i	x_i	P_i(x)= ε⁽ⁱ⁾₀	ε⁽ⁱ⁾₁	ε⁽ⁱ⁾₂	ε⁽ⁱ⁾₃	ε⁽ⁱ⁾₄
0	2,71828182845904	1	-2,39221119117733	0,705207033512282	-61,0702755830021	0,693879569827545
1	1	0,581976706869326	5,72267438319407	0,69023539353372	121,870014050176	0,692833802968095
2	1	0,756720180469139	-9,31836050756016	0,695317144633344	-146,585461084686
3	1	0,649405165216329	5,20217803449192	0,690925043467957
4	0.5	0,777556616828803	-2,49324571003365
5	0.5	0,51016754082086

La valeur de P₅(2), pourtant située dans l'intervalle d'interpolation, est assez éloignée de ln(2), valeur de la fonction à interpoler. Sur le graphique, on note une forte dégradation des qualités d'interpolation du polynôme entre 1.5 et e. La présence d'un pôle à proximité de l'intervalle d'interpolation, ainsi que la croissance logarithmique de la courbe se prête mal à l'interpolation par polynômes. Ceci se prête davantage à l'interpolation rationnelle. L'application de l'ε-algorithme d'interpolation à ce polynôme améliore significativement les qualités d'interpolation sur cet exemple. Sur le graphique, certaines fractions rationnelles obtenues sont presque indiscernable de la fonction à interpoler, dans l'intervalle d'interpolation, et au delà. Les nombres en gras dans la table de l'ε-algorithme représente les fraction rationnelles d'interpolation de degré 5/0, 4/1 et 3/2. Elle peut être continuée pour intégrer celles de degré 2/3, 1/4 et 0/5.

Accélération de la convergence des série de Fourier et de Tchebychev

Les sommes partielles des séries de Fourier ou de Tchebychev peuvent fournir une suite qui peut être accélérée par l'ε-algorithme. Cependant, une manière plus efficace de procéder est de transformer, par un changement de variable, ces séries en une série entière. Les sommes partielles de ces séries entières seront les donnés d'entrée pour l'ε-algorithme.

La série de Fourier :

f(\theta )={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }(a_{n}\cos {n\theta }+b_{n}\sin {n\theta })

ou celle de Tchebychev:

f(x)={\frac {c_{0}}{2}}+\sum _{n=1}^{\infty }c_{n}T_{n}(x)

se transforment chacune en une série entière (d'une variable complexe)

F(z)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }(a_{n}-\mathrm {i} b_{n})z^{n}{\text{ avec }}z=\mathrm {e} ^{\mathrm {i} \theta }

F(z)={\frac {c_{0}}{2}}+\sum _{n=1}^{\infty }c_{n}z^{n}{\text{ avec }}z=\mathrm {e} ^{\mathrm {i} \theta };\theta =Arcos(x)

dont la partie réelle est la série d'origine. Les T_n(x) représentent les polynômes de Tchebychev de 1ère espèce.

Ces séries se prêtent idéalement à l'accélération de la convergence par l'ε-algorithme (avec des nombres complexes) sur leurs sommes partielles. La partie réelle du résultat sera la valeur accélérée de la série de Fourier ou de Tchebychev d'origine.

Par exemple, la fonction Logarithme sur $[1, 9]$ , dont la série de Tchebychev vaut[4] :

\ln(1+8x)-2\ln 2=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{n.2^{n-1}}}T_{n}(y)\qquad avec\ y=2x-1\qquad 0\leqslant x\leqslant 1

devient après changement de variable la série entière :

f(z)-2\ln 2=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}z^{n}}{n.2^{n-1}}}{\text{ avec }}z=\mathrm {e} ^{\mathrm {i} \theta };\theta =Arcos(2x-1)

Le graphique ci contre compare la fonction Logarithme avec sa série de Tchebychev en retenant les termes jusqu'au degré 6, ainsi que la valeur accélérée de cette série partielle par l'ε-algorithme. On note une nette amélioration de la convergence (erreur divisée par 80 ou plus). Le résultat accéléré conserve les caractéristiques typiques des approximations de Tchebychev: les oscillations d'amplitudes approximativement égales de l'erreur sur l'intervalle concerné (à peine perceptible sur le graphique).

Accélération de la convergence de série de Tchebychev de ln(x) par l ε-algorithme

Formellement, l'ε-algorithme transforme la série auxiliaire en approximant de Padé. En explicitant les calculs, l'approximant de Padé ici vaut:

f(z)-2\ln 2={\frac {22z^{3}+240z^{2}+480z}{3z^{3}+72z^{2}+360z+480}}

dont la partie réelle, en revenant à la variable d'origine, vaut:

\ln(1+8x)\simeq 2\ln 2+{\frac {14080x^{3}+83040x^{2}+107328x+21862}{3840x^{3}+47520x^{2}+129744x+97971}}

Cette fraction a les caractéristiques proches de la fraction min-max, optimale pour l'approximation: elle peut fournir un bon point de départ pour initialiser l'algorithme de Remez rationnel.

Variante des méthodes utilisant l'extrapolation de Richardson

Plusieurs méthodes numériques utilisent l'extrapolation de Richardson pour accélérer la convergence de méthodes d'ordre peu élevé. On trouve par exemple son utilisation dans :

- l'évaluation de la dérivée d'une fonction, par accélération de la convergence de la méthode des différences centrales ;
- l'intégration numérique, en accélérant la méthode des trapèzes (méthode de Romberg) ou la méthode du point médian ;
- l'intégration des équations différentielles, en accélérant la méthode du point milieu (méthode de Gragg-Bulirsch-Stoer).

Dans chacune de ces applications, il est possible de remplacer l'extrapolation de Richardson par l'ε-algorithme ou ses généralisations. La suite associée $x n$ devant tendre vers l'infini dans le cas des généralisations de l'ε-algorithme, on prendra l'inverse de la suite associée à l'extrapolation de Richardson. Cependant l'extrapolation de Richardson étant particulièrement bien adaptée à accélérer les suites générées par ces méthodes, l'ε-algorithme en général est moins performant. Dans certains cas, par exemple le calcul numérique d'une intégrale impropre, l'extrapolation de Richardson échoue à accélérer la convergence, et l'ε-algorithme devient alors la méthode de choix[5].

Par exemple, l'intégrale

$\int _{0}^{1}{\sqrt {x}}dx={\frac {2}{3}}=0,66666666666...$

possède une singularité algébrique en zéro, qui ralentit la convergence de la méthode de Romberg. L'utilisation de l'ε-algorithme à la place de l'extrapolation de Richardson dans cette méthode donne de meilleurs résultats :

Méthode de Romberg et l'ε-algorithme avec une intégrale impropre
subdivisions	Trapèzes	Romberg	ε-algorithme
1	0,5	0,5	0,5
2	0,603553390593274	0,638071187457699	0,603553390593274
4	0,643283046242747	0,657756603281563	0,668014371343285
8	0,658130221624454	0,663607569112292	0,666989411481855
13	0,663581196877228	0,665592865129466	0,666661304912164
32	0,665558936278942	0,666287699033842	0,666666280204189
64	0,666270811378507	0,666532741199894	0,666666671581115

Notes et références

(en) P. Wynn, « On a device for computing the e_m(S_n) transformation », MTAC, 10 (1956), p. 91-96.
(en) Guido Claessens, Some aspects of the rational Hermite interpolation table and its applications : Ph. D. thesis, Université d'Anvers, 1976.
(en) Peter Wynn, « Singular rules for certain non-linear algorithms », BIT, vol. 3,‎ 1963, p. 175–195 (DOI 10.1007/BF01939985, lire en ligne).
Yudell Luke, « On the computation of Log Z and Arc tan Z », Mathematical Tables and Other Aids to Computation, vol. 11,‎ 1957, p. 16-18
David K. Kahaner, « An Numerical quadrature by the ε-algorithm », Mathematics of computation, vol. 36,‎ 1972, p. 689-693

Voir aussi

Bibliographie

Claude Brezinski, Algorithmes d'accélération de la convergence : étude numérique, éditions Technip, 1978, (ISBN 2-7108-0341-0)

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.