Accueil🇫🇷Chercher

Empilement Pi

En chimie, l' empilement pi (également appelé empilement π – π ) fait référence à des interactions attractives et non-covalentes entre les cycles aromatiques, car ils contiennent des liaisons pi . Ces interactions sont importantes dans l'empilement de nucléobases dans les molécules d' ADN et d' ARN, le repliement des protéines, la synthèse dirigée par matrice, la science des matériaux et la reconnaissance moléculaire, bien que certaines recherches[1] suggèrent que l'empilement pi peut ne pas être opérationnel dans certaines de ces applications. Malgré un intérêt expérimental et théorique intense, il n'y a pas de description unifiée des facteurs qui contribuent aux interactions d'empilement pi.


Trois conformations du dimère de benzène

Preuve de l'empilement pi

Le dimère de benzène est le système prototypique pour l'étude de l'empilement pi, et est lié expérimentalement par 8–12 kJ/mol (2–3 kcal/mol) en phase gazeuse avec une séparation de 4,96 Å entre les centres de masse pour le dimère en forme de T. La faible énergie de liaison rend le dimère de benzène difficile à étudier expérimentalement, et le dimère lui-même n'est stable qu'à basse température et a tendance à se regrouper[2].

Une autre preuve de l'empilement pi provient de la détermination de la structure cristalline aux rayons X. Des configurations parallèles, perpendiculaires et décalées peuvent être observées dans les structures cristallines de nombreux composés aromatiques simples[2]. Des géométries parallèles ou perpendiculaires décalées similaires ont été observées dans une étude des structures cristallines de protéines aux rayons X à haute résolution dans la banque de données sur les protéines[3]. L'analyse des acides aminés aromatiques phénylalanine, tyrosine, histidine et tryptophane indique que les dimères de ces chaînes latérales ont de nombreuses interactions de stabilisation possibles à des distances plus grandes que les rayons moyens de van der Waals[4].

Configurations géométriques

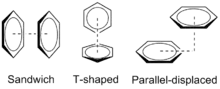
Les géométries préférées du dimère de benzène ont été modélisées à un niveau élevé de théorie avec des calculs MP2-R12 / A et de très grands ensembles de base aug-cc-PVTZ corrigés contre le contrepoids[2]. Les deux conformations les plus stables sont le parallèle déplacé et en forme de T, qui sont essentiellement isoénergétiques. En revanche, la configuration sandwich maximise le chevauchement du système pi, ce qui déstabilise l'interaction. La configuration sandwich représente un point de selle énergétique, ce qui est cohérent avec la rareté relative de cette configuration dans les données de cristal de rayons X.

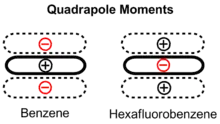
Moments quadripolaires du benzène et de l'hexafluorobenzène. La polarité est inversée en raison des différences d'électronégativité pour l'hydrogène et le fluor par rapport au carbone.

Les énergies de liaison relatives de ces trois configurations géométriques du dimère de benzène peuvent être expliquées par un équilibre des forces quadripolaire / quadripolaire et des forces de London. Bien que le benzène n'ait pas de moment dipolaire, il a un moment quadripolaire fort[5]. Le dipôle C – H local signifie qu'il y a une charge positive sur les atomes dans le cycle et une charge négative correspondante représentant un nuage d'électrons au-dessus et au-dessous du cycle. Le moment quadripolaire est inversé pour l' hexafluorobenzène en raison de l'électronégativité du fluor. Le dimère de benzène dans la configuration sandwich est stabilisé par les forces de dispersion de London mais déstabilisé par des interactions répulsives quadripolaires / quadripolaires. En décalant l'un des anneaux benzéniques, la configuration parallèle déplacée réduit ces interactions répulsives et est stabilisée. La grande polarisabilité des cycles aromatiques conduit à des interactions dispersives comme contribution majeure aux effets d'empilement. Ceux-ci jouent un rôle majeur pour les interactions des nucléobases, par exemple dans l' ADN[6]. La configuration en forme de T bénéficie d'interactions quadripolaires / quadripolaires favorables, car le quadripôle positif d'un anneau benzénique interagit avec le quadripôle négatif de l'autre. Les anneaux benzéniques sont les plus éloignés dans cette configuration, de sorte que les interactions quadripolaires / quadripolaires favorables compensent évidemment la diminution des forces de dispersion .

Effets de substitution

La capacité d'ajuster les interactions d'empilement pi serait utile dans de nombreux efforts de synthèse. Un exemple serait d'augmenter l'affinité de liaison d'un inhibiteur de petite molécule à une poche d'enzyme contenant des résidus aromatiques. Les effets des hétéroatomes[3] et des substituants sur les interactions d'empilement pi sont difficiles à modéliser et font débat.

Modèle électrostatique

Un premier modèle pour le rôle des substituants dans les interactions d'empilement pi a été proposé par Hunter et Sanders[7]. Ils ont utilisé un modèle mathématique simple basé sur les charges atomiques sigma et pi, les orientations relatives et les interactions de van der Waals pour déterminer qualitativement que l'électrostatique est dominante dans les effets de substitution. Selon leur modèle, les groupes attracteurs d'électrons réduisent le quadripôle négatif du cycle aromatique et favorisent ainsi les conformations parallèles déplacées et les conformations sandwich. En revanche, les groupes donneurs d'électrons augmentent le quadripôle négatif, ce qui peut augmenter la force d'interaction dans une configuration en forme de T avec la géométrie appropriée. Sur la base de ce modèle, les auteurs ont proposé un ensemble de règles régissant les interactions d'empilement pi qui prévalaient jusqu'à ce que des calculs plus sophistiqués soient appliqués.

Les preuves expérimentales du modèle Hunter – Sanders ont été fournies par Siegel et al. en utilisant une série de 1,8-di-o-tolylnaphtalènes substitués syn et anti[8]. Dans ces composés, les groupes aryle "s'affrontent" dans une géométrie empilée en raison de l'encombrement stérique, et la barrière d'épimérisation a été mesurée par spectroscopie de résonance magnétique nucléaire. Les auteurs ont rapporté que les cycles aryles avec des substituants attracteurs d'électrons avaient des barrières plus élevées à la rotation. L'interprétation de ce résultat était que ces groupes réduisaient la densité électronique des cycles aromatiques, permettant des interactions d'empilement sandwich pi plus favorables et donc une barrière plus élevée. En d'autres termes, les groupes attracteurs d'électrons ont conduit à des interactions électrostatiques "moins défavorables" à l'état fondamental.

Cycle de double mutant utilisé par Hunter et al. [9] pour sonder les interactions d'empilement π en forme de T

Hunter et coll. ont appliqué un cycle de double mutant chimique plus sophistiqué avec une «fermeture éclair» à liaison hydrogène pour résoudre la question des effets de substituant dans les interactions d'empilement pi[9]. Cette technique a été utilisée pour étudier une multitude d'interactions non-covalentes. La mutation unique, dans ce cas, le changement d'un substituant sur un cycle aromatique, entraîne des effets secondaires tels qu'un changement de la force de la liaison hydrogène. La double mutation quantifie ces interactions secondaires, de sorte que même une faible interaction d'intérêt peut être disséquée du tableau. Leurs résultats indiquent que davantage de substituants attracteurs d'électrons ont des interactions d'empilement pi moins répulsives. En conséquence, cette tendance a été exactement inversée pour les interactions avec le pentafluorophénylbenzène, qui a un moment quadripolaire égal en magnitude mais de signe opposé à celui du benzène[5]. Les résultats fournissent des preuves directes du modèle Hunter – Sanders. Cependant, les interactions d'empilement mesurées à l'aide de la méthode du double mutant étaient étonnamment petites, et les auteurs notent que les valeurs peuvent ne pas être transférables à d'autres systèmes.

Dans une étude de suivi, Hunter et al. ont vérifié en première approximation que les énergies d'interaction des anneaux aromatiques en interaction dans un double cycle mutant sont dominées par des effets électrostatiques[10]. Cependant, les auteurs notent que les interactions directes avec les substituants du cycle, discutées ci-dessous, apportent également des contributions importantes. En effet, l'interaction de ces deux facteurs peut entraîner le comportement compliqué dépendant des substituants et de la géométrie des interactions d'empilement pi.

Modèle d'interaction directe

Le modèle Hunter-Sanders a été critiqué par de nombreux groupes de recherche offrant des preuves contradictoires, expérimentales et informatiques, des interactions d'empilement pi qui ne sont pas principalement régies par des effets électrostatiques.

La preuve expérimentale la plus claire contre les effets des substituants électrostatiques a été rapportée par Rashkin et Waters[11]. Ils ont utilisé des bromures de N-benzyl-2-(2-fluorophényl)-pyridinium substitués en méta et para, qui s'empilent dans une conformation déplacée parallèle, comme système modèle pour les interactions d'empilement pi. Dans leur système, un lieur méthylène interdit les interactions favorables en forme de T. Comme dans les modèles précédents, la force relative des interactions d'empilement pi a été mesurée par RMN comme le taux de rotation autour de la liaison biaryle, car les interactions d'empilement pi sont perturbées dans l'état de transition. Les anneaux para-substitués avaient de petites barrières de rotation qui augmentaient avec les groupes de plus en plus attracteurs d'électrons, conformément aux résultats antérieurs. Cependant, les cycles méta-substitués avaient des barrières de rotation beaucoup plus grandes malgré des densités d'électrons presque identiques dans le cycle aromatique. Les auteurs expliquent cette divergence comme une interaction directe du bord des atomes d'hydrogène d'un cycle avec les substituants électronégatifs sur l'autre cycle. Cette affirmation est étayée par les données de déplacement chimique du proton en question.

Une grande partie des analyses détaillées des contributions relatives des facteurs dans l'empilement pi ont été confirmées par le calcul. Sherill et Sinnokrot ont rapporté une découverte surprenante utilisant une théorie selon laquelle tous les dimères de benzène substitués ont des interactions de liaison plus favorables qu'un dimère de benzène dans la configuration sandwich[12]. Des travaux de calcul ultérieurs du groupe Sherill ont révélé que les effets des substituants pour la configuration sandwich sont additifs, ce qui indique une forte influence des forces de dispersion et des interactions directes entre les substituants[13]. Il a été noté que les interactions entre benzènes substitués dans la configuration en forme de T étaient plus complexes. Enfin, Sherill et Sinnokrot affirment dans leur article que tout semblant de tendance basée sur des substituants donneurs ou retirants d'électrons peut être expliqué par des termes de répulsion d'échange et de dispersion[14].

Modèle de calcul de Houk et Wheeler[15] des interactions directes des substituants dans l'empilement pi.

Houk et Wheeler fournissent également des preuves informatiques convaincantes de l'importance de l'interaction directe dans l'empilement pi[15]. Dans leur analyse des dimères de benzène substitués dans une conformation sandwich, ils ont pu récapituler leurs résultats en utilisant un modèle extrêmement simple où le benzène substitué, Ph – X, a été remplacé par H – X. Fait remarquable, ce modèle brut a abouti à la même tendance des énergies d'interaction relatives, et est fortement corrélé aux valeurs calculées pour Ph – X. Cette découverte suggère que les effets de substituant dans le dimère de benzène sont dus à une interaction directe du substituant avec le cycle aromatique, et que le système pi du benzène substitué n'est pas impliqué. Ce dernier point est développé ci-dessous.

En résumé, il semblerait que les contributions relatives des interactions électrostatiques, de dispersion et des interactions directes aux effets de substitution observés dans les interactions d'empilement pi dépendent fortement de la géométrie et de la conception expérimentale. L'absence de consensus sur la question peut simplement refléter la complexité de la question.

Exigence d'aromaticité

La compréhension conventionnelle de l'empilement pi implique des interactions quadripolaires entre les électrons délocalisés dans les orbitales p. En d'autres termes, l'aromaticité doit être requise pour que cette interaction se produise. Cependant, plusieurs groupes ont fourni des preuves contraires, remettant en question si l'empilement pi est un phénomène unique ou s'il s'étend à d'autres molécules neutres.

Dans une expérience non différente des autres mentionnées ci-dessus, Paliwal et ses coauteurs ont construit une balance de torsion moléculaire à partir d'un ester arylique avec deux états conformationnels[16]. L'état plié avait une interaction d'empilement pi bien définie avec une géométrie en forme de T, alors que l'état déplié n'avait pas d'interactions aryl-aryle. Les déplacements chimiques RMN des deux conformations étaient distincts et pouvaient être utilisés pour déterminer le rapport des deux états, qui était interprété comme une mesure des forces intramoléculaires. Les auteurs rapportent qu'une préférence pour l'état replié n'est pas unique aux esters d'aryle. Par exemple, l'ester cyclohexylique a favorisé l'état replié plus que l'ester phénylique, et l'ester tert-butylique a favorisé l'état replié d'une préférence supérieure à celle montrée par tout ester arylique. Cela suggère que l'aromaticité n'est pas une exigence stricte pour une interaction favorable avec un cycle aromatique.

D'autres preuves des résultats d'interactions d'empilement pi non aromatiques comprennent des études critiques en chimie théorique, expliquant les mécanismes sous-jacents des observations empiriques. Grimme a rapporté que les énergies d'interaction de dimères plus petits constitués d'un ou deux cycles sont très similaires pour les composés aromatiques et saturés. Cette découverte est particulièrement pertinente pour la biologie et suggère que la contribution des systèmes pi à des phénomènes tels que les nucléobases empilées pourrait être surestimée. Cependant, il a été montré qu'une interaction stabilisante accrue est observée pour les grands dimères aromatiques. Comme indiqué précédemment, cette énergie d'interaction dépend fortement de la géométrie. En effet, les grands dimères aromatiques ne sont stabilisés par rapport à leurs homologues saturés que dans une géométrie sandwich, alors que leurs énergies sont similaires dans une interaction en forme de T.

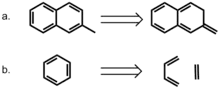
a) Naphtalènes substitués et b) Dissection homodésmotique du benzène utilisée par Bloom et Wheeler[17] pour quantifier les effets de la délocalisation sur l'empilement pi.

Une approche plus directe de la modélisation du rôle de l'aromaticité a été adoptée par Bloom et Wheeler[17]. Les auteurs ont comparé les interactions entre le benzène et le 2-méthylnaphtalène ou son isomère non aromatique, le 2-méthylène-2,3-dihydronaphtalène. Ce dernier composé permet de conserver le nombre d'électrons p tout en supprimant les effets de délocalisation. Étonnamment, les énergies d'interaction avec le benzène sont plus élevées pour le composé non aromatique, ce qui suggère que la localisation de la liaison pi est favorable dans les interactions d'empilement pi. Les auteurs ont également envisagé une dissection homodesmotique du benzène en éthylène et 1,3-butadiène et ont comparé ces interactions dans un sandwich avec du benzène. Leur calcul indique que l'énergie d'interaction entre le benzène et le benzène homodesmotique est supérieure à celle d'un dimère de benzène dans les conformations en sandwich et parallèles déplacées, soulignant à nouveau la favorabilité des interactions localisées de liaison pi. Ces résultats suggèrent fortement que l'aromaticité n'est pas requise pour les interactions d'empilement pi dans ce modèle.

Même à la lumière de ces preuves, Grimme conclut que l'empilement pi existe bel et bien[18]. Cependant, il avertit que les plus petits anneaux, en particulier ceux dans des conformations en forme de T, se comportent de manière similaire à leurs homologues saturés, et que le terme devrait être spécifié pour les plus grands anneaux dans des conformations empilées qui semblent présenter un effet d'électrons pi coopératif.

Applications
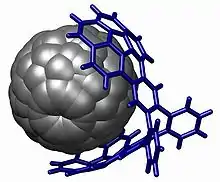
Un fullerène lié dans un buckycatcher par des interactions d'empilement aromatiques[19].

Une démonstration puissante de l'empilement se trouve dans le buckycatcher[19]. Cette pince moléculaire est basée sur deux corannulènes concaves avec un ajustement parfait pour une molécule de fullerène convexe. La complexation a lieu simplement en évaporant une solution de toluène contenant les deux composés. En solution, une constante d'association de 8600 M−1 est mesurée sur la base des changements des déplacements chimiques RMN.

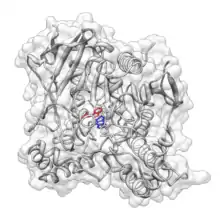
Tacrine liée à l'acétylcholinestérase (PDB 1ACJ). Une interaction d'empilement pi entre la tacrine (bleu) et Trp84 (rouge) est proposée.

L'empilement pi est répandu dans les structures cristallines des protéines et contribue également aux interactions entre les petites molécules et les protéines. En conséquence, les interactions pi – pi et cation – pi sont des facteurs importants dans la conception rationnelle des médicaments[20]. Un exemple est la tacrine, inhibiteur de l'acétylcholinestérase (AChE) approuvé par la FDA, qui est utilisé dans le traitement de la maladie d'Alzheimer . Il est proposé que la tacrine ait une interaction d'empilement pi avec l'anneau indolique de Trp84, et cette interaction a été exploitée dans la conception rationnelle de nouveaux inhibiteurs de l'AChE[21].

Ajout de composés pharmacologiques actifs
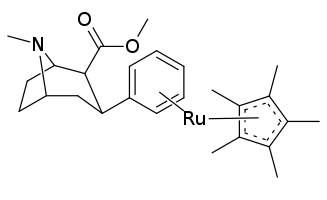
Analogue de cocaïne 21b, un antagoniste

Plusieurs variantes de phényles coordonnés pi ont même été testées en utilisant des métaux de transition pour l'empilement de η 6 -phényltropanes, en utilisant du cyclopentadiényle et du tricarbonyle à la place d'un benzène. Ceci, dans le cas du tricarbonyle, a doublé l'affinité du composé pour son site de ligand prévu (posé comme étant dû aux influences électrostatiques résultantes étant plus propices à la cible)[22].

En assemblage supramoléculaire
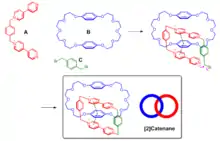
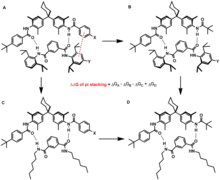
Figure 2. La synthèse de Stoddart du [2] caténane.

Les systèmes π sont des éléments de base importants dans l'assemblage supramoléculaire en raison de leurs interactions non-covalentes polyvalentes avec divers groupes fonctionnels. Un exemple notable d'application des interactions π – π dans l'assemblage supramoléculaire est la synthèse de caténane. L'enjeu majeur de la synthèse de caténane est de verrouiller les molécules de manière contrôlée. Stoddart et ses collègues ont développé une série de systèmes utilisant les fortes interactions π – π entre les dérivés du benzène riches en électrons et les cycles pyridinium pauvres en électrons[23]. Le [2] catanène a été synthétisé en faisant réagir le bis(pyridinium) (A), le bisparaphénylène-34-couronne-10 (B) et le 1,4-bis (bromométhyl) benzène (C) (Fig. 2). L'interaction π – π entre A et B a dirigé la formation d'un intermédiaire gabarit imbriqué qui a été cyclisé davantage par réaction de substitution avec le composé C pour générer le produit [2] caténane.

Voir également

Les références
  1. (en) Martinez et Iverson, « Rethinking the term “pi-stacking” », Chemical Science, vol. 3, no 7,‎ , p. 2191 (ISSN 2041-6520, DOI 10.1039/c2sc20045g, lire en ligne)
  2. Sinnokrot, Valeev et Sherrill, « Estimates of the ab initio limit for pi–pi interactions: The benzene dimer », J. Am. Chem. Soc., vol. 124, no 36,‎ , p. 10887–10893 (PMID 12207544, DOI 10.1021/ja025896h)
  3. Huber, Margreiter, Fuchs et von Grafenstein, « Heteroaromatic π-Stacking Energy Landscapes », Journal of Chemical Information and Modeling, vol. 54, no 5,‎ , p. 1371–1379 (PMID 24773380, DOI 10.1021/ci500183u)
  4. McGaughey, Gagné et Rappé, « Pi-Stacking interactions. Alive and well in proteins », J. Biol. Chem., vol. 273, no 25,‎ , p. 15458–15463 (PMID 9624131, DOI 10.1074/jbc.273.25.15458)
  5. Battaglia, Buckingham et Williams, « The electric quadrupole moments of benzene and hexafluorobenzene », Chem. Phys. Lett., vol. 78, no 3,‎ , p. 421–423 (DOI 10.1016/0009-2614(81)85228-1, Bibcode 1981CPL....78..421B)
  6. Riley et Hobza, « On the Importance and Origin of Aromatic Interactions in Chemistry and Biodisciplines », Acc. Chem. Res., vol. 46, no 4,‎ , p. 927–936 (DOI 10.1021/ar300083h)
  7. Hunter et Sanders, « The nature of π–π Interactions », J. Am. Chem. Soc., vol. 112, no 14,‎ , p. 5525–5534 (DOI 10.1021/ja00170a016)
  8. Cozzi, Cinquini, Annuziata et Siegel, « Dominance of polar/.pi. Over charge-transfer effects in stacked phenyl interactions », J. Am. Chem. Soc., vol. 115, no 12,‎ , p. 5330–5331 (DOI 10.1021/ja00065a069)
  9. Cockroft, Hunter, Lawson et Perkins, « Electrostatic control of aromatic stacking interactions », J. Am. Chem. Soc., vol. 127, no 24,‎ , p. 8594–8595 (PMID 15954755, DOI 10.1021/ja050880n)
  10. Cockroft, Perkins, Zonta et Adams, « Substituent effects on aromatic stacking interactions », Org. Biomol. Chem., vol. 5, no 7,‎ , p. 1062–1080 (PMID 17377660, DOI 10.1039/b617576g, lire en ligne)
  11. Rashkin et Waters, « Unexpected substituent effects in offset pi–pi stacked interactions in water », J. Am. Chem. Soc., vol. 124, no 9,‎ , p. 1860–1861 (PMID 11866592, DOI 10.1021/ja016508z)
  12. Sinnokrot et Sherrill, « Unexpected Substituent Effects in Face-to-Face π-Stacking Interactions », J. Phys. Chem. A, vol. 107, no 41,‎ , p. 8377–8379 (DOI 10.1021/jp030880e, Bibcode 2003JPCA..107.8377S)
  13. Ringer, Sinnokrot, Lively et Sherrill, « The effect of multiple substituents on sandwich and T-shaped pi–pi interactions », Chem. Eur. J., vol. 12, no 14,‎ , p. 3821–8 (PMID 16514687, DOI 10.1002/chem.200501316)
  14. Sinnokrot et Sherrill, « High-accuracy quantum mechanical studies of pi–pi interactions in benzene dimers », J. Phys. Chem. A, vol. 110, no 37,‎ , p. 10656–10668 (PMID 16970354, DOI 10.1021/jp0610416, Bibcode 2006JPCA..11010656S)
  15. Wheeler et Houk, « Substituent effects in the benzene dimer are due to direct interactions of the substituents with the unsubstituted benzene », J. Am. Chem. Soc., vol. 130, no 33,‎ , p. 10854–10855 (PMID 18652453, PMCID 2655233, DOI 10.1021/ja802849j)
  16. Paliwal, Geib et Wilcox, « Molecular Torsion Balance for Weak Molecular Recognition Forces. Effects of "Tilted-T" Edge-to-Face Aromatic Interactions on Conformational Selection and Solid-State Structure », J. Am. Chem. Soc., vol. 116, no 10,‎ , p. 4497–4498 (DOI 10.1021/ja00089a057)
  17. Bloom et Wheeler, « Taking the Aromaticity out of Aromatic Interactions », Angew. Chem., vol. 123, no 34,‎ , p. 7993–7995 (DOI 10.1002/ange.201102982)
  18. Grimme, « Do Special Noncovalent π–π Stacking Interactions Really Exist? », Angew. Chem. Int. Ed., vol. 47, no 18,‎ , p. 3430–3434 (DOI 10.1002/anie.200705157)
  19. A. Sygula, F. R. Fronczek, R. Sygula, P. W. Rabideau and M. M. Olmstead, « A Double Concave Hydrocarbon Buckycatcher », J. Am. Chem. Soc., vol. 129, no 13,‎ , p. 3842–3843 (PMID 17348661, DOI 10.1021/ja070616p)
  20. Babine et Bender, « Molecular Recognition of Proteinminus signLigand Complexes: Applications to Drug Design », Chem. Rev., vol. 97, no 5,‎ , p. 1359–1472 (PMID 11851455, DOI 10.1021/cr960370z)
  21. Da Silva et al., « Molecular modeling, docking and ADMET studies applied to the design of a novel hybrid for treatment of Alzheimer's disease », J. Mol. Graphics Modell., vol. 25, no 2,‎ , p. 169–175 (PMID 16413803, DOI 10.1016/j.jmgm.2005.12.002)
  22. Singh et al., « Chemistry, Design, and Structure-Activity Relationship of Cocaine Antagonists », Chem. Rev., vol. 100, no 3,‎ , p. 925–1024 (PMID 11749256, DOI 10.1021/cr9700538, lire en ligne)
  23. Ashton, Goodnow, Kaifer et Reddington, « A [2] Catenane Made to Order », J. Angew. Chem. Int. Ed., vol. 28, no 10,‎ , p. 1396–1399 (DOI 10.1002/anie.198913961)

Liens externes
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.