Dureté d'un graphe
En théorie des graphes, la dureté (« toughness » en anglais) est une mesure de la connexité d'un graphe.
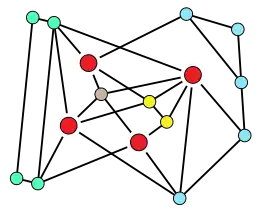
Principe
Un graphe G est dit t-dur pour un nombre réel donné t si, pour tout entier k > 1, G ne peut être divisé en k composantes connexes par la suppression de moins de tk sommets. Par exemple, un graphe est 1-dur si le nombre de composantes connexes obtenues en supprimant un ensemble de sommets est toujours au moins aussi grand que le nombre de sommets supprimés. La dureté d'un graphe est le plus grand nombre t maximum pour lequel il est t-solide; c'est un nombre fini pour tous les graphes finis, à l'exception des graphes complets qui par convention ont une ténacité infinie.
La notion de dureté du graphe a été introduite pour la première fois par Václav Chvátal en 1973[1]. Depuis lors, de nombreux travaux sur la dureté ont été publiés ; un article de synthèse de Bauer, Broersma & Schmeichel de 2006[2] répertorie 99 théorèmes et 162 articles sur le sujet.
Exemples
La suppression de k sommets d'un graphe chemin peut diviser le graphe restant en au plus k + 1 composantes connexes. Le maximum du rapport entre le nombre de composantes et le nombre de sommets supprimés est obtenu en supprimant un sommet à l'intérieur du chemin ce qui le divise en deux composantes. Par conséquent, les chemins sont 12 -durs. En revanche, la suppression de k sommets d'un graphe cycle laisse au plus k composantes connexes, et laisse parfois exactement k composantes connexes, de sorte qu'un cycle est 1-dur.
Lien avec la connectivité des sommets
Si un graphe est t-dur, alors on obtient, en fixant k = 2 est que tout ensemble de 2t − 1 sommets peut être supprimé sans diviser le graphe en deux. Autrement dit, un graphe t-dur est également 2t-sommet-connexe .
Lien avec la hamiltonicité
Chvátal 1973 a observé que tout graphe cycle, et donc toute chaîne hamiltonienne, est 1-dur ; par conséquent, être 1-dur est une condition nécessaire pour qu'un graphe soit hamiltonien. Il a conjecturé qu'il existe un seuil t tel que tout graphe t-dur est hamiltonien. La conjecture originale de Chvátal avec t = 2 aurait donné une démonstration du théorème de Fleischner mais a été réfutée par Bauer, Broersma & Veldman en 2000[3]. L'existence d'un seuil de dureté plus grand pour les graphes hamiltonien est un problème ouvert.
Complexité de calcul
Tester si un graphe est 1-dur est co-NP-complet. En d'autres termes, le problème de décision dont la réponse est "oui" pour un graphe qui n'est pas 1-solide, et "non" pour un graphe qui est 1-dur, est NP-complet. Il en est de même pour tout nombre rationnel positif fixe q : tester si un graphe est q-dur est co-NP-complet[4].
Notes et références
Bibliographie
- [2021] Xiaofeng Gu, « A Proof of Brouwer's Toughness Conjecture », SIAM Journal on Discrete Mathematics, vol. 35, no 2, , p. 948–952 (DOI 10.1137/20M1372652)
- [2020] Mark Norman Ellingham, Pouria Salehi Nowbandegani et Songling Shan, « Toughness and prism-hamiltonicity of P4-free graphs », Discrete Applied Mathematics, vol. 284, , p. 201–206 (DOI 10.1016/j.dam.2020.03.035)
- [2020] Davin Park, Anthony Ostuni, Nathan Hayes, Amartya Banerjee, Tanay Wakhare, Wiseley Wong et Sebastian Cioabă, « The Toughness of Kneser Graphs », Arxiv preprint, (arXiv 2008.08183).
- [2006] Douglas Bauer, Hajo J. Broersma et Edward Schmeichel, « Toughness in graphs—a survey », Graphs and Combinatorics, vol. 22, no 1, , p. 1–35 (DOI 10.1007/s00373-006-0649-0, MR 2221006, S2CID 3237188).
- [2000] Douglas Bauer, Hajo J. Broersma et Henk Jan Veldman, « Not every 2-tough graph is Hamiltonian », Discrete Applied Mathematics, vol. 99, nos 1–3, , p. 317–321 (DOI 10.1016/S0166-218X(99)00141-9, MR 1743840, lire en ligne).
- [1996] Douglas Bauer, Seifollah Louis Hakimi et Edward Schmeichel, « Recognizing tough graphs is NP-hard », Discrete Applied Mathematics, vol. 28, no 3, , p. 191–195 (DOI 10.1016/0166-218X(90)90001-S, MR 1074858).
- [1973] Václav Chvátal, « Tough graphs and Hamiltonian circuits », Discrete Mathematics, vol. 5, no 3, , p. 215–228 (DOI 10.1016/0012-365X(73)90138-6, MR 0316301).
Notions connexes
- Force d'un graphe, un concept analogue pour les suppressions d'arêtes
- Formule de Tutte-Berge, une caractérisation liée à la taille d'un couplage maximal dans un graphe.
- Lexique de la théorie des graphes