Division en galère

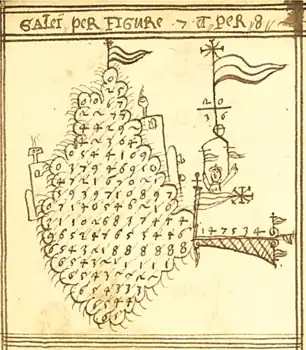
La division en galère est parfois improprement dite "de Galley"[1], galley n'étant pas une personne, mais la traduction en anglais de l'italien galea. Niccolo Tartaglia décrit son processus dans La prima parte del general trattato di numeri, et misure.. en 1556 où il le nomme per Batello ou per Galea en référence à la figure obtenue lorsque le travail est terminé. En anglais on trouve aussi la dénomination "scratch division" parce que les chiffres sont rayés au fur et à mesure de leur utilisation.
Elle fait son apparition en Europe en même temps que les chiffres arabes et Leonardo Fibonacci la pratiquait dès 1202^{[référence souhaitée]}. Elle est également mentionnée dans l'arithmétique de Trévise en 1478. Dans le Moyen-Orient, Al-Kwarizmi utilisait en 825 une version antérieure de cette méthode ^{[référence souhaitée]} et selon Lam Lay Yong, son origine remonte au I^er siècle de notre ère dans la Chine ancienne[2].

La division en galère était encore utilisée en France au XVIII^e siècle[3] jusqu'à la Révolution quand l'algorithme de la potence en usage actuellement l'a supplantée petit à petit.

La figure de référence est extraite d'un manuscrit vénitien datant de la fin du XVI^e siècle[4]. Elle présente la division de ${\displaystyle 965\;347\;653\;446}$ par ${\displaystyle 6\;543\;218}$ : on lit le quotient ${\displaystyle 147\;534}$ et le reste ${\displaystyle 529\;074}$. La preuve par 9 présentée sous le drapeau n'est pas équilibrée. Elle met en évidence une faute de calcul, le reste juste étant ${\displaystyle 529\;034}$.

Voici la description de l'algorithme appliqué à la division de 117 121 par 563 :

Les étapes de la division en galère de 117121 par 563

a) On écrit l'un sous l'autre le dividende et le diviseur. ${\displaystyle 117<563}$ donc on écrit ${\displaystyle 563}$ sous ${\displaystyle 1171}$ avec un alignement à droite. On ménage une place à droite pour écrire le quotient. Les chiffres seront rayés au fur et à mesure de leur utilisation et on veillera à bien les placer en colonnes.

b) ${\displaystyle 1171}$ contient ${\displaystyle 2}$ fois ${\displaystyle 563}$ : le premier chiffre du quotient est ${\displaystyle 2}$. On remultiplie de gauche à droite pour déterminer les restes :

${\displaystyle 11-2\times 5=1}$ : on raye ${\displaystyle 5}$ et ${\displaystyle 11}$ et on écrit le reste ${\displaystyle 1}$.

c) ${\displaystyle 17-2\times 6=5}$ : on raye ${\displaystyle 6}$ et ${\displaystyle 17}$ et on écrit le reste ${\displaystyle 5}$.

d) ${\displaystyle 51-2\times 3=45}$ : on raye ${\displaystyle 3}$ et ${\displaystyle 51}$ et on écrit le reste ${\displaystyle 45}$.

e) On décale le diviseur d'un cran vers la droite puis on passe au chiffre suivant du quotient : ${\displaystyle 452<563}$ donc ce chiffre est ${\displaystyle 0}$.

f) On raye ${\displaystyle 563}$ pour le décaler d'un cran vers la droite. On passe au chiffre suivant du quotient : ${\displaystyle 4521}$ contient ${\displaystyle 8}$ fois ${\displaystyle 563}$ : le chiffre suivant est ${\displaystyle 8}$.

g) ${\displaystyle 45-8\times 5=5}$ : on raye ${\displaystyle 5}$ et ${\displaystyle 45}$ et on écrit le reste ${\displaystyle 5}$.

h) ${\displaystyle 52-8\times 6=4}$ : on raye ${\displaystyle 6}$ et ${\displaystyle 52}$ et on écrit le reste ${\displaystyle 4}$.

i) ${\displaystyle 41-8\times 3=17}$ : on raye ${\displaystyle 3}$ et ${\displaystyle 41}$ et on écrit le reste ${\displaystyle 17}$.

La division euclidienne est terminée, le quotient entier est ${\displaystyle 208}$ et le reste est ${\displaystyle 17}$.
On pourrait continuer en plaçant une virgule au quotient et en ajoutant des zéros au dividende.

Les ouvrages d'arithmétique du XVI^e siècle[5] présentent une méthode d'extraction de racine carrée semblable à la division en galère moyennant quelques aménagements. Il s'agit d'un algorithme qui fournit l'un après l'autre les chiffres de la racine carrée d'un entier donné en écriture décimale :
On commence par regrouper les chiffres du radicande deux par deux, quitte à ajouter un zéro à gauche s'ils sont en nombre impair. On calcule ensuite successivement les chiffres de la racine carrée en reconstituant le radicande par concaténation de la gauche vers la droite par groupes de deux chiffres (voir l'exemple qui suit).

Étapes du calcul de la racine carrée de 74 602.

Si ${\displaystyle a}$ est la partie entière de la racine carrée de ${\displaystyle A}$ avec un reste ${\displaystyle R}$, on cherche à l'étape suivante le plus grand chiffre ${\displaystyle b}$ tel que : ${\displaystyle (10a+b)^{2}\leqslant 100A+B}$ où ${\displaystyle B}$ est le nombre formé des deux chiffres suivants.
Cette inégalité peut s'écrire : ${\displaystyle (10a+b)^{2}\leqslant 100(a^{2}+R)+B}$
ou encore : ${\displaystyle 100a^{2}+2\times 10a\times b+b^{2}\leqslant 100a^{2}+100R+B}$
c'est-à-dire : ${\displaystyle (2\times 10a+b)\times b\leqslant 100R+B}$
Le problème se ramène à la division de ${\displaystyle 100R+B}$ par ${\displaystyle 2\times 10a+b}$.

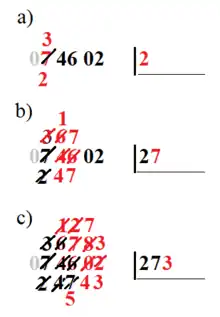
Exemple : Calcul de la racine carrée de ${\displaystyle 74\;602}$.
Le regroupement des chiffres deux par deux donne ${\displaystyle 07|46|02|}$

a) La racine carrée de ${\displaystyle 7}$ est ${\displaystyle 2}$ et il reste ${\displaystyle 7-2\times 2=3}$.

b) On cherche le plus grand chiffre ${\displaystyle b}$ tel que ${\displaystyle (2\times 20+b)\times b\leqslant 346}$ : c'est ${\displaystyle b=7}$, puis on calcule le reste : ${\displaystyle 346-7\times 47=17}$.

c) On cherche le plus grand chiffre ${\displaystyle b}$ tel que ${\displaystyle (2\times 270+b)\times b\leqslant 1702}$ : c'est ${\displaystyle b=3}$, puis on calcule le reste : ${\displaystyle 1702-3\times 543=73}$.

La partie entière de la racine carrée de ${\displaystyle 74\;602}$ est ${\displaystyle 273}$ et il reste ${\displaystyle 73}$.

On pourrait alors continuer par le calcul des décimales en plaçant une virgule et en rajoutant des paires de zéros au radicande.

• 
  Un trois-mâts inventé par Tartaglia
• 
  Animation de la construction de Tartaglia
• 
  Calcul d'une racine carrée

• Niccolo Tartaglia, La prima parte del general trattato di numeri, et misure, Venise 1556. Accessible en ligne
• Jeanne Guillet, Une petite histoire de la division : de la méthode de Galley à la méthode actuelle, IREM de Grenoble 1994. Accessible en ligne.

• (en)/(es) Cet article est partiellement ou en totalité issu des articles intitulés en anglais « Galley division » (voir la liste des auteurs) et en espagnol « División por galera » (voir la liste des auteurs).