Distance de diamètre angulaire

La distance de diamètre angulaire est une notion utilisée en cosmologie pour exprimer la distance apparente d’un objet astronomique à partir de son diamètre angulaire. Il ne s’agit pas de la distance réelle à laquelle se situe l’objet en question (voir ci-dessous). La distance de diamètre angulaire fait partie des différentes distances que l’on peut associer aux objets astrophysiques, au même titre que la distance de luminosité et la distance propre.

Introduction

Dans un univers en expansion, le concept de distance devient plus ambigu. Par exemple, une galaxie lointaine qui émet sa lumière à une certaine époque va avoir le temps de s’éloigner de nous avant que nous en recevions la lumière. Ainsi, au moment où nous recevons la lumière de cet objet, la distance qui nous sépare de lui n’est plus la même que celle à l’époque où il a émis sa lumière. Tant que la variation de distance de l’objet est faible entre l’émission et la réception de sa lumière, le concept de distance a un sens relativement explicite. Par contre, dès que la variation de distance de l’objet est significative lors du trajet de la lumière, le concept de « distance » doit donc être précisé. En pratique, la limite entre ces deux situations se produit pour des distances de l’ordre du rayon de Hubble, soit une fraction significative de la taille de l’univers observable.

Dans la vie courante

Ordinairement, il existe une relation simple entre la taille angulaire θ d’un objet, sa taille réelle d et sa distance D à l’observateur. Si l’on exprime θ en radians, alors cette relation s’écrit, dans la limite où la taille angulaire est faible (quelques degrés ou moins) :

\theta ={\frac {d}{D}}

En pratique, si l’on connaît la taille réelle d de l’objet, la mesure de sa taille angulaire θ permet de déduire sa distance à l’observateur.

Cas d'un univers en expansion

Dans ce cas il faudra utiliser une métrique adaptée en l'occurrence celle de Robertson & Walker

Importance pour la cosmologie

En pratique, la quantité facilement mesurable en plus du diamètre angulaire est le décalage vers le rouge. Pour un modèle cosmologique donné, il existe une relation entre distance de l’objet à l’époque où il a émis sa lumière et son décalage vers le rouge. Cette relation, qui fait intervenir une quantité appelée temps conforme, dépend du contenu matériel de l’univers.

En pratique, la difficulté est plutôt de trouver une classe d’objets astrophysiques dont la taille réelle soit connue. De tels objets sont habituellement appelés règle standard (standard rod ou standard ruler en anglais). Il n’existe cependant pas beaucoup d’objets suffisamment uniformes et bien compris aujourd’hui pour que leur taille réelle puisse être prédite avec certitude (voir ci-dessous).

Tests par la distance angulaire

Radiogalaxies

Une des premières règles standard dont l’utilisation a été envisagée a été les lobes observés dans certaines radiogalaxies géantes. Cependant ce genre de test n’a pour l’heure pas été probant. Une autre tentative a été faite à l’aide des grands vides présents entre les super amas de galaxie. La théorie de la formation des grandes structures indique que la répartition de la matière dans l’univers est homogène au-delà d’une certaine échelle. Cette échelle est donnée par la taille des plus grands vides. Ces vides n’ont pas de taille fixe au cours du temps car ils subissent l’expansion de l’univers. Cependant, la variation de leur taille est connue. On peut donc en principe les utiliser non pas comme règle standard, mais comme « règle standardisable »[1]. Cette méthode n’a pour l’heure pas permis d’obtenir des résultats très précis et ne fait donc pas l’objet d’investigation approfondie.

Fond diffus cosmologique

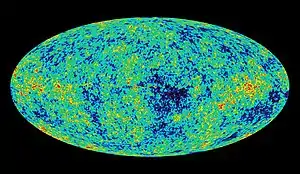
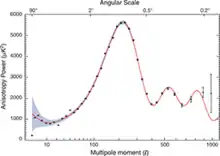
La granularité de la carte des anisotropies du fond diffus cosmologique révèle la taille angulaire de l’horizon sonore à l’époque de la recombinaison.

La taille angulaire de l’horizon sonore apparaît encore plus clairement sur le spectre de puissance de la carte de WMAP ci-dessus sous la forme de la bosse appelée pic Doppler correspondant à l’échelle angulaire d’environ un degré.

Un test par contre considérablement plus contraignant peut être utilisé avec le fond diffus cosmologique. Le fond diffus cosmologique représente la lumière émise par l’univers tout entier au moment où sa densité est devenue suffisamment basse pour permettre à la lumière de s’y propager librement. Cette époque, dite de la recombinaison correspond à un décalage vers le rouge d’environ 1100, et se situe seulement 380 000 ans après le Big Bang. L’étude du fond diffus cosmologique révèle que celui-ci est extrêmement uniforme, mais présente de petites fluctuations de densité, qui sont les germes des grandes structures (galaxies, amas de galaxies, etc) observées aujourd’hui. L’étude de ces fluctuations, appelées perturbations cosmologiques permet de prédire qu’il existe une taille limite à ces fluctuations au-delà de laquelle elles ne peuvent avoir eu le temps d’évoluer de façon significative à l’époque où la lumière du fond diffus cosmologique a été émise. Cette taille caractéristique est appelée horizon sonore, concrètement elle représente la distance maximum que peut avoir parcouru une onde sonore depuis le Big Bang. Cette taille caractéristique apparaît dans les anisotropies du fond diffus cosmologique comme la taille angulaire des « granularités » qui apparaissent sur la carte.

Le fond diffus cosmologique représente l’objet le plus lointain de l’univers visible dans le spectre électromagnétique. Il est donc particulièrement adapté à un test de type distance angulaire pour différencier des modèles dont la distance angulaire varie de façon notable à grande distance. À ce titre, le test le plus efficace porte sur les contraintes que l’on peut mettre sur la courbure spatiale de l’univers (voir ci-dessous), car un modèle dont la courbure spatiale est non nulle voit sa distance angulaire varier de façon considérable par rapport à un modèle dont la courbure spatiale est nulle dès que l’on se place à des échelles supérieures au rayon de courbure.

La taille angulaire de l’horizon sonore permet ainsi de placer des contraintes très fortes sur la courbure spatiale. Ce résultat a été mis en évidence de manière détaillée pour la première fois grâce à l’expérience BOOMERanG en 2000[2]. Depuis l’arrivée des données du satellite WMAP en 2003, les contraintes sur la courbure spatiale ont pu être affinées[3]. Dans le cadre du modèle standard de la cosmologie, Ce genre de test permet de contraindre le paramètre de densité de l’univers à des valeurs très proches 1, et par suite contraindre le rayon de courbure à être significativement plus grand que la taille de l’univers observable et par conséquent bien plus grand que le rayon de Hubble.

Voir aussi

Liens externes

Notes et références

Boudewijn F. Roukema & Gary A. Mamon, Tangential Large Scale Structure as a Standard Ruler: Curvature Parameters from Quasars, Astronomy and Astrophysics 358 (2000) 395, astro-ph/9911413 voir en ligne.
Paolo de Bernardis et al., A Flat Universe from High-Resolution Maps of the Cosmic Microwave Background Radiation, Nature 404 (2000) 955-959, astro-ph/0004404 voir en ligne.
Voir les résultats des analyses des données de WMAP en 2003 puis 2006 :
- David N. Spergel et al., First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters, The Astrophysical Journal Supplément 148 (2003) 17, astro-ph/0302209 voir en ligne
- David N. Spergel et al., Wilkinson Microwave Anisotropy Probe (WMAP) Three Year Results: Implications for Cosmology, à paraître, astro-ph/0603449 Voir en ligne.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.