Distance d'un point à une droite
En géométrie euclidienne, la distance d'un point à une droite est la plus courte distance séparant ce point et un point courant de la droite. Le théorème de Pythagore permet d'affirmer que la distance du point A à la droite (d ) correspond à la distance séparant A de son projeté orthogonal Ah sur la droite (d ).
On peut ainsi écrire :

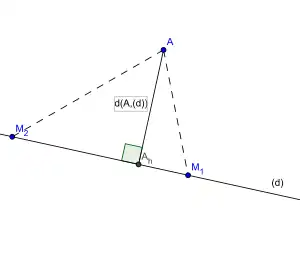
La distance entre le point A et la droite (d ) est la distance AAh
Dans le plan
Si le plan est muni d'un repère orthonormal, si la droite (d) a pour équation ax + by + c = 0 et si le point A a pour coordonnées (xA ; yA), alors la distance entre A et (d ) est donnée par la formule

En effet, si M(x, y ) est un point quelconque de la droite (d ), et si on note  le vecteur normal à la droite (d ) de composantes (a ; b ), alors la valeur absolue du produit scalaire des vecteurs
le vecteur normal à la droite (d ) de composantes (a ; b ), alors la valeur absolue du produit scalaire des vecteurs  et
et  est donnée par les deux expressions :
est donnée par les deux expressions :
 ( ax + by = - c car M est un point de (d))
( ax + by = - c car M est un point de (d)) .
.
En particulier :
- si la droite a pour équation y = mx + p alors
 ;
;
- si la droite a pour équation x = a alors

- si la droite est donnée par son équation normale:
 alors
alors  (où, bien entendu
(où, bien entendu  et
et  ). La distance d'un point à une droite est tout simplement la valeur absolue de ce polynôme pour les coordonnées du point A. Dire qu'un point appartient à une droite (d) ssi ses coordonnées en vérifient l'équation, cela revient à affirmer que sa distance à (d) est nulle.
). La distance d'un point à une droite est tout simplement la valeur absolue de ce polynôme pour les coordonnées du point A. Dire qu'un point appartient à une droite (d) ssi ses coordonnées en vérifient l'équation, cela revient à affirmer que sa distance à (d) est nulle.
Remarque : Si l'on considère la distance algébrique (id. si elle est comptée avec son signe), le polynôme  (avec
(avec  ) peut prendre des valeurs positives, négatives ou nulles selon que le point est au-delà[1], en deçà ou sur la droite considérée. Le signe de cette distance algébrique divise le plan en trois domaines, deux demi-plans et une droite, un peu à la manière de la puissance d'un point par rapport à un cercle qui divise le cercle en trois zones (l'intérieur du cercle, le cercle et l'extérieur du cercle).
) peut prendre des valeurs positives, négatives ou nulles selon que le point est au-delà[1], en deçà ou sur la droite considérée. Le signe de cette distance algébrique divise le plan en trois domaines, deux demi-plans et une droite, un peu à la manière de la puissance d'un point par rapport à un cercle qui divise le cercle en trois zones (l'intérieur du cercle, le cercle et l'extérieur du cercle).
Dans l'espace
Si l'espace est muni d'un repère orthonormé, si la droite (d ) passe par le point B et a pour vecteur directeur  , la distance entre le point A et la droite (d) est donnée par la formule
, la distance entre le point A et la droite (d) est donnée par la formule

où  représente le produit vectoriel des vecteurs
représente le produit vectoriel des vecteurs  et
et  et où
et où  représente la norme du vecteur
représente la norme du vecteur  .
.
En effet, si l'on note C le point de (d ) tel que  alors l'aire du triangle ABC est donnée par les deux expressions
alors l'aire du triangle ABC est donnée par les deux expressions

 .
.
Cette distance est supérieure ou égale à toute distance séparant le point A d'un plan contenant la droite (d ). Si la droite (d ) est définie comme l'intersection de deux plans perpendiculaires et si l'on note d₁ et d₂ les distances du point A à ces deux plans, on a :
 .
.
En dimension n
Si l'espace est muni d'un repère orthonormal, si la droite (d) passe par le point B et a pour vecteur directeur  . Tout point
. Tout point  peut être écrit ainsi
peut être écrit ainsi

La distance entre le point A et la droite (d) se trouve en calculant la distance AM avec M le point de (d) le plus proche de A. Cela revient à trouver t

où  représente le produit scalaire des vecteurs
représente le produit scalaire des vecteurs  et
et  .
On a donc
.
On a donc

Démonstration :
Cela revient à trouver  qui minimise
qui minimise  . Minimiser
. Minimiser  revient au même (la fonction carrée est strictement croissante du côté positif).
revient au même (la fonction carrée est strictement croissante du côté positif).

On cherche  , pour trouver ce minimum.
, pour trouver ce minimum.



Voir aussi
Notes et références
- Rem: le point est dit «au-delà» de la droite s'il n'est pas dans le même demi-plan que l'origine par rapport à cette droite.
Cet article est issu de
wikipedia. Text licence:
CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.




































