Dilemme biais-variance
En statistique et en apprentissage automatique, le dilemme (ou compromis) biais–variance est le problème de minimiser simultanément deux sources d'erreurs qui empêchent les algorithmes d'apprentissage supervisé de généraliser au-delà de leur échantillon d'apprentissage :
- Le biais est l'erreur provenant d’hypothèses erronées dans l'algorithme d'apprentissage. Un biais élevé peut être lié à un algorithme qui manque de relations pertinentes entre les données en entrée et les sorties prévues (sous-apprentissage).
- La variance est l'erreur due à la sensibilité aux petites fluctuations de l’échantillon d'apprentissage. Une variance élevée peut entraîner un surapprentissage, c'est-à-dire modéliser le bruit aléatoire des données d'apprentissage plutôt que les sorties prévues.
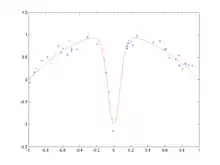
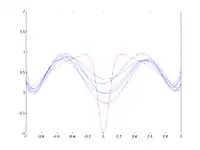
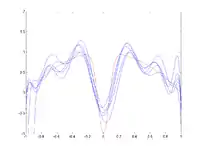
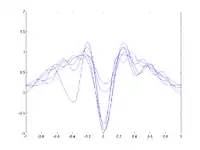
Pour chaque essai, quelques points de données bruitées sont fournis comme ensemble d'apprentissage (en haut).
Pour une forte valeur du paramètre d'envergure (spread) (image 2), le biais est élevé : les RBFs ne peuvent pleinement approximer la fonction (en particulier le creux central), mais la variance entre les différents essais est faible. Lorsque le paramètre d'envergure diminue (image 3 et 4), le biais diminue : les courbes bleues se rapprochent davantage de la courbe rouge. Cependant, en fonction du bruit dans les différents essais, la variance entre les essais augmente. Dans l'image du bas, les approximations pour x = 0 varient énormément selon l'endroit où se trouvaient les points de données.La décomposition biais-variance est une façon d'analyser l'espérance de l'erreur de prédiction d'un algorithme d'apprentissage d'un problème particulier comme une somme de trois termes : le biais, la variance et une quantité, appelée erreur irréductible, résultant du bruit dans le problème lui-même.
Ce compromis s'applique à toutes les formes d'apprentissage supervisé : classification, régression (fonction de montage)[1] - [2], et le structured (output) learning (en). Il a également été invoqué pour expliquer l'efficacité des heuristiques dans l'apprentissage humain.
Motivation
Le compromis biais-variance est un problème central en apprentissage supervisé. Idéalement, on veut choisir un modèle qui reflète avec précision les régularités dans les données d'apprentissage, mais qui se généralise aussi aux données tests (données n'ayant pas servi à apprendre le modèle). Malheureusement, il est généralement impossible de faire les deux en même temps. Les méthodes d'apprentissage avec une variance élevée peuvent assez bien représenter l’échantillon d’apprentissage, mais il existe un risque de surapprentissage sur des données tests ou bruitées. En revanche, les algorithmes avec une variance faible produisent généralement des modèles plus simples qui n'ont pas tendance au sur-apprentissage, mais peuvent être en sous-apprentissage sur le jeu de données d'apprentissage.
Les modèles avec un faible biais sont généralement plus complexes (par exemple la régression polynomiale à plusieurs degrés), mais permettent de représenter les données d’apprentissage avec plus de précision. Cependant, ils peuvent également représenter une partie du bruit aléatoire du jeu d'apprentissage, leurs prédictions sont donc moins précises malgré la complexité supplémentaire. En revanche, les modèles avec un biais plus élevé ont tendance à être relativement simples (régression polynomiale à moindre degré ou même linéaire), mais peuvent produire des prédictions de variance plus faible lorsqu'ils sont appliqués au-delà de l'ensemble d'apprentissage.
Décomposition biais-variance de l'erreur quadratique
Supposons que nous avons un ensemble d'apprentissage constitué d'un ensemble de points et de valeurs réelles associée à chaque point . Nous supposons qu'il existe une relation fonctionnelle bruitée , où le bruit, , a une moyenne nulle et une variance .
Trouver une fonction qui se généralise à des points extérieurs à l'ensemble d'apprentissage peut être fait avec l'un des nombreux algorithmes utilisés pour l'apprentissage supervisé. Selon la fonction que nous choisissons, son erreur attendue sur un échantillon test peut se décomposer comme suit[3]:34 - [4]:223:
où
et
L'espérance est calculée sur l'ensemble des différents choix de l'échantillon d'apprentissage , tous générés selon la même distribution. Les trois termes sont :
- le biais au carré de la méthode d'apprentissage, qui peut être vue comme l'erreur due aux hypothèses simplifiées de la méthode utilisée. Par exemple, approcher une fonction non linéaire à l'aide d'une méthode pour modèle linéaire va produire des erreurs d'estimation du fait de cette hypothèse ;
- la variance de la méthode d'apprentissage, ou plus intuitivement, de combien la méthode d'apprentissage se déplace autour de sa moyenne;
- l'erreur irréductible . Étant donné que tous les trois termes sont positifs, cela constitue une limite inférieure sur l'erreur attendue sur des échantillons test[3].:34
Plus le modèle de est complexe, plus le biais sera faible. Cependant, la complexité va rendre le modèle "mobile" pour s'adapter aux données, et donc sa variance sera plus grande.
Application à la classification
La décomposition biais-variance a été initialement formulée pour une régression des moindres carrés. Dans le cas de la classification sous la perte 0-1 (Taux d'erreur), Il est possible de trouver une décomposition similaire [7] - [8]. Sinon, si le problème de la classification peut être formulé comme classification probabiliste, alors l'erreur quadratique attendue des probabilités prédites par rapport aux véritables probabilités peut être décomposée comme précédemment[9].
Approches
La réduction de la dimension et la sélection de variables (features en anglais) peuvent diminuer la variance tout en simplifiant les modèles. De même, un plus grand ensemble d'apprentissage tend à diminuer la variance. L'ajout de variables explicatives (features) tend à diminuer le biais, au détriment de l'introduction de variance supplémentaire.
Les algorithmes d'apprentissage ont généralement certains paramètres ajustables qui contrôlent le biais et la variance, e.g. :
- Les modèles linéaires généralisés peuvent être régularisés afin d'en diminuer la variance mais au prix de l'augmentation du biais[10].
- Avec les réseaux de neurones, la variance augmente et le biais diminue avec le nombre de couches cachées[1]. Comme dans le modèle linéaire généralisé, une régularisation est généralement appliquée.
- Avec la méthode des k plus proches voisins, une valeur élevée de k conduit à un biais élevé et une variance faible (voir ci-dessous).
- Avec la méthode d'Instance-based learning (en), la régularisation peut être obtenue en variant le mélange de prototypes et modèles[11].
- Avec les arbres de décision, la profondeur de l'arbre détermine la variance. Les arbres de décision sont généralement élagués pour contrôler la variance[3].:307
Une façon de résoudre le compromis consiste à utiliser des modèles mixte et de l'apprentissage ensembliste[12] - [13]. Par exemple, le boosting combine plusieurs "mauvais" modèles (biais élevé) dans un ensemble qui a un biais plus faible que les modèles individuels, tandis que le bagging combine les "meilleurs" classifieurs d'une manière qui réduit leur variance.
Méthode des k plus proches voisins
Dans le cas de la méthode des k plus proches voisins, une formule explicite existe concernant la décomposition biais–variance du paramètre [4]:
où sont les plus proches voisins de dans l’échantillon d'apprentissage. Le biais (premier terme de l’équation) est une fonction monotone croissante de , alors que la variance (second terme) diminue lorsque augmente. En effet, avec des "hypothèses raisonnables", le biais de l'estimateur du plus proche voisin (1-NN) disparaît entièrement lorsque la taille de l’échantillon d'apprentissage tend vers l'infini[1].
Application à l'apprentissage humain
Bien que largement discuté dans le contexte de l'apprentissage automatique, le dilemme biais-variance a été examiné dans le contexte des sciences cognitives, et plus particulièrement par Gerd Gigerenzer et ses co-auteurs dans le contexte de l'apprentissage heuristique. Ils soutiennent que le cerveau humain résout ce dilemme dans le cas des généralement parcimonieux sur des ensembles mal caractérisés fournies par une expérience en adoptant une heuristique biais élevé/faible variance. Cela reflète le fait qu'une approche non biaisée se généralise mal à de nouvelles situations, et suppose aussi déraisonnablement une connaissance précise de la réalité. Les heuristiques en résultant sont relativement simples, mais produisent de meilleures inférences dans une plus grande variété de situations[14].
Geman et al. soutiennent que le dilemme biais-variance implique que les capacités telles que la reconnaissance d'objet générique ne peuvent être apprises à partir de zéro, mais nécessitent un certain degré d'inné qui est ensuite réglée par l'expérience. Ceci car les approches sans modèle d'inférence nécessitent des ensembles d'apprentissage démesurément grands si l'on veut éviter une forte variance.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bias–variance tradeoff » (voir la liste des auteurs).
- Geman, Stuart; E. Bienenstock; R. Doursat (1992).
- Bias–variance decomposition, In Encyclopedia of Machine Learning.
- Gareth James; Daniela Witten; Trevor Hastie; Robert Tibshirani (2013).
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009).
- Vijayakumar, Sethu (2007).
- Shakhnarovich, Greg (2011).
- Domingos, Pedro (2000).
- Valentini, Giorgio; Dietterich, Thomas G. (2004).
- Manning, Christopher D.; Raghavan, Prabhakar; Schütze, Hinrich (2008).
- Belsley, David (1991).
- Gagliardi, F (2011).
- Jo-Anne Ting, Sethu Vijaykumar, Stefan Schaal, Locally Weighted Regression for Control.
- Scott Fortmann-Roe.
- Gigerenzer, Gerd; Brighton, Henry (2009).
Liens externes
- Scott Fortmann-Roe, « Understanding the Bias-Variance Tradeoff »,








![{\displaystyle {\begin{aligned}\mathrm {E} \left[\left(y-{\hat {f}}(x)\right)^{2}\right]&=\mathrm {Biais} \left[{\hat {f}}(x)\right]^{2}+\mathrm {Var} \left[{\hat {f}}(x)\right]+\sigma ^{2}\\\end{aligned}}}](https://img.franco.wiki/i/2947461631a74a154f6da6a3f91f0fe498d149fa.svg)
![{\displaystyle {\begin{aligned}\mathrm {Biais} \left[{\hat {f}}(x)\right]=\mathrm {E} \left[{\hat {f}}(x)-f(x)\right]\end{aligned}}}](https://img.franco.wiki/i/9ea78f291090869b0e83987304f7706b743cf5c2.svg)
![{\displaystyle {\begin{aligned}\mathrm {Var} \left[{\hat {f}}(x)\right]=\mathrm {E} \left[\left({\hat {f}}(x)-\mathrm {E} [{\hat {f}}(x)]\right)^{2}\right]\end{aligned}}}](https://img.franco.wiki/i/8b7cc24047b536def6fc7fe6a6cafa0d2d0942bc.svg)





![{\displaystyle {\begin{aligned}\mathrm {Var} [X]=\mathrm {E} [X^{2}]-\mathrm {E} [X]^{2}\end{aligned}}}](https://img.franco.wiki/i/f13fdb9db4a119c8d00e220bb7cf51637b1792a4.svg)
![{\displaystyle {\begin{aligned}\mathrm {E} [X^{2}]=\mathrm {Var} [X]+\mathrm {E} [X]^{2}\end{aligned}}}](https://img.franco.wiki/i/e4a8980facc6722d88b8350bf04230d428ec245c.svg)

![{\displaystyle {\begin{aligned}\mathrm {E} [f]=f\end{aligned}}}](https://img.franco.wiki/i/8cd3852100c919ebb3c8a3085ed8e14268d0393f.svg)

![{\displaystyle \mathrm {E} [\epsilon ]=0}](https://img.franco.wiki/i/f7494dee92fe5ac5a8d8a61fa72e73482ad679d9.svg)
![{\displaystyle \mathrm {E} [y]=\mathrm {E} [f+\epsilon ]=\mathrm {E} [f]=f}](https://img.franco.wiki/i/6a027bc2f4ced7f9af72c462a548d72d285aa788.svg)
![{\displaystyle \mathrm {Var} [\epsilon ]=\sigma ^{2}}](https://img.franco.wiki/i/4ed97af78f7548bb5ebb8ae3a04101a3c8a25511.svg)
![{\displaystyle {\begin{aligned}\mathrm {Var} [y]=\mathrm {E} [(y-\mathrm {E} [y])^{2}]=\mathrm {E} [(y-f)^{2}]=\mathrm {E} [(f+\epsilon -f)^{2}]=\mathrm {E} [\epsilon ^{2}]=\mathrm {Var} [\epsilon ]+\mathrm {E} [\epsilon ]^{2}=\sigma ^{2}\end{aligned}}}](https://img.franco.wiki/i/459eaadae3f6c660fbefa85b4c14ef1d3e78c444.svg)

![{\displaystyle {\begin{aligned}\mathrm {E} \left[(y-{\hat {f}})^{2}\right]&=\mathrm {E} \left[y^{2}+{\hat {f}}^{2}-2y{\hat {f}}\right]\\&=\mathrm {E} [y^{2}]+\mathrm {E} \left[{\hat {f}}^{2}\right]-\mathrm {E} [2y{\hat {f}}]\\&=\mathrm {Var} [y]+\mathrm {E} [y]^{2}+\mathrm {Var} [{\hat {f}}]+\mathrm {E} [{\hat {f}}]^{2}-2f\mathrm {E} [{\hat {f}}]\\&=\mathrm {Var} [y]+\mathrm {Var} [{\hat {f}}]+(f-\mathrm {E} [{\hat {f}}])^{2}\\&=\mathrm {Var} [y]+\mathrm {Var} [{\hat {f}}]+\mathrm {E} [f-{\hat {f}}]^{2}\\&=\sigma ^{2}+\mathrm {Var} [{\hat {f}}]+\mathrm {Biais} [{\hat {f}}]^{2}.\end{aligned}}}](https://img.franco.wiki/i/fb5044a73c743637f4b4a3af2386a012e254349f.svg)

![{\displaystyle \mathrm {E} [(y-{\hat {f}}(x))^{2}]=\left(f(x)-{\frac {1}{k}}\sum _{i=1}^{k}f(N_{i}(x))\right)^{2}+{\frac {\sigma ^{2}}{k}}+\sigma ^{2}}](https://img.franco.wiki/i/2852b9b12eb56a64c35b4eb49b9e3b19b665da2f.svg)
