Dôme géodésique
En architecture, un dôme géodésique est une structure sphérique, ou partiellement sphérique, en treillis dont les barres suivent les grands cercles (géodésiques) de la sphère. L'intersection des barres géodésiques forme des éléments triangulaires qui possèdent chacun leur propre rigidité, provoquant la distribution des forces et des tensions sur l'ensemble de la structure qui est de ce fait autoporteuse, laissant l'intérieur entièrement disponible (pas de piliers).

La construction des coupoles géodésiques a été particulièrement développée par l'architecte américain Richard Buckminster Fuller. L'une de ses géodes les plus remarquables est un dôme géodésique transparent de 80 m de diamètre qui fut construit sur l'île Sainte-Hélène à Montréal en 1967 pour être le pavillon des États-Unis à l'exposition universelle de Montréal et qui abrite aujourd'hui la Biosphère.
La forme mathématique de la structure d'un dôme géodésique est une géode. Généralement, son polyèdre générateur est un icosaèdre inscrit dans une sphère hypothétique, orienté de telle sorte que l'un de ses 12 sommets (ou le centre de l'une de ses 20 faces) se trouve au point le plus haut de l'édifice. Ceci présente un intérêt non seulement esthétique, mais aussi pratique pendant la phase de construction de la structure (un mât central vertical permettant de soulever l'ouvrage au fur et à mesure que de nouveaux éléments lui sont ajoutés). Chaque face de l'icosaèdre est pavée par des triangles plus petits : le plus simple est de diviser chaque côté en N parties égales, et de paver chaque face par N² triangles équilatéraux. Puis, les sommets de chaque triangle sont projetés sur la sphère inscrite, de manière à transformer chaque triangle en triangle sphérique.
Quelque 300 000 dômes géodésiques ont été construits à travers le monde. Ils peuvent servir à de très nombreux usages : lieux publics (musées, lieux d'exposition, salles de spectacle, lieux de compétition sportive ou d'entraînement…), centres commerciaux, structures provisoires (forums, expositions, salons, tentes collectives ou individuelles…), habitations collectives (expéditions scientifiques…), structures à usage technique, abris divers (entrepôts, hangars, garages, couverture de réservoirs, abris de jardin), et même habitations privées (bien que cet usage présente de sérieux (en) inconvénients)…

Il est exceptionnel qu'un dôme géodésique soit complet : le plus souvent, on n'en construit que la partie supérieure et il est d'usage d'indiquer par une fraction simple (et donc approximative) le rapport entre la hauteur de la structure et le diamètre de la sphère circonscrite au polyèdre générateur.
En toute rigueur, on devrait appeler « sphère géodésique » les dômes complets, et réserver la dénomination de « dôme géodésique » ou « coupole géodésique » aux dômes incomplets.
Procédés de construction
Géodes renforcées
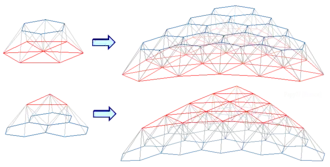
Quand une géode est de grandes dimensions, il peut être intéressant, au point de vue architectural, d'en renforcer la cohésion en superposant deux coupoles géodésiques, duales l'une de l'autre. Il y a deux façons de réaliser ce renforcement :
- on peut placer une géode normale « à l'extérieur » du bâtiment et la doubler « à l'intérieur » d'une géode duale, ou au contraire
- on peut placer une géode normale « à l'intérieur » du bâtiment et la doubler « à l'extérieur » d'une géode duale, ce qui est généralement considéré comme plus satisfaisant sur le plan esthétique.
Le principe de ce renforcement consiste :
- à prendre un groupe de 6 faces triangles (d'une géode normale) ayant un sommet commun et de bâtir sur la base de chacun de ces 6 triangles une pyramide (à 6 faces) dont le sommet, situé à l'aplomb du centre du triangle, est relié à chaque sommet du triangle servant de base par des arêtes dont la longueur est proche de la moyenne des longueurs des arêtes de la géode normale ; on relie ensuite les sommets de ces 6 pyramides de façon à former un hexagone qui constitue l'une des faces de la géode duale qui double la géode normale ; ou encore, mais cela revient au même, le renforcement consiste :
- à prendre un groupe de 3 faces hexagonales (d'une géode duale) ayant un sommet commun et de bâtir sur la base de chacun de ces 3 hexagones une pyramide (à 12 faces) dont le sommet, situé à l'aplomb du centre de l'hexagone, est relié à chaque sommet de l'hexagone servant de base par des arêtes dont la longueur est proche de la moyenne des distances entre les centres des faces adjacentes de la géode duale ; on relie ensuite les sommets de ces 3 pyramides de façon à former un triangle qui constitue l'une des faces de la géode normale qui est ainsi doublée par la géode duale.
Le schéma ci-dessus montre, dans sa partie supérieure, une géode normale intérieure doublée d'une géode duale extérieure, et dans sa partie inférieure, une géode normale extérieure doublée d'une géode duale intérieure.
Impression 3D
Chuck Hoberman a démontré la possibilité de réaliser une structure de dôme géodésique pliable, rendu possible par un processus d'impression 3D permettant de concevoir des charnières et des raccords complexes, directement imprimés en leur position finale et fonctionnelle[1].
Remarques diverses
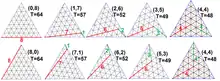
Dans la typologie qu'il a établie, l'architecte américain Richard Buckminster Fuller nomme « fréquence » d'une géode le nombre minimum de segments reliant deux sommets d'un triangle de pavage. Ce dernier étant subdivisé en petits triangles dont les côtés sont ces segments. La fréquence peut s'écrire sous la forme d'une somme a + b, où a et b sont les nombres de segments selon deux directions distinctes.
Il distingue 3 classes de dômes géodésiques : les dômes les plus simples (avec b = 0) correspondent à la classe I (ils sont dits « triacon »), ceux de la classe II correspondent aux cas où a = b (ils sont dits « alternate »), et enfin la classe III englobe tous les dômes dits « twisted » (c'est-à-dire tournants ou tors en français) pour lesquels b n'est ni nul ni égal à a. Mais selon d'autres sources (ou auteurs), les classes I et II correspondraient respectivement aux cas a = b (« alternate ») et b = 0 (« triacon »)
Certains auteurs contestent que Fuller soit l'inventeur des dômes géodésiques et justifient leur point de vue en rappelant que dès 1922, l'ingénieur Walther Bauersfeld (en), travaillant chez Zeiss, a eu l'idée d'une structure de type V-1-1 duale pour la construction, à Iena, du premier planétarium ouvert au public. Toutefois, il semble bien que Bauersfeld n'ait vu dans cette idée que la solution d'un problème optique et qu'il n'ait pas entrevu la possibilité d'une généralisation de cette idée à la construction de vastes bâtiments à usage général.
Il semble qu'aucun dôme géodésique de classe III et de grandes dimensions n'ait été réalisé par un architecte, probablement parce que la construction en est un peu plus compliquée, sans contrepartie d'ordre esthétique…
De même, aucun dôme géodésique correspondant à N = 3 ou à N = 4 n'a été construit par un architecte ; ceci s'explique aisément par la très grande dispersion des longueurs des arêtes, celle-ci entraînant à la fois une beaucoup plus grande fragilité et une esthétique assez peu agréable, surtout lorsque N = 3 ; ces dômes sont donc de pures curiosités mathématiques !
De même, et pour les mêmes raisons, aucune géode quadrillée (à base de cubes) n'a été construite !
Quelques géodes remarquables
Voici, classés par ordre de diamètre décroissant, les dômes géodésiques parmi plus grands au monde. Ceux-ci sont cependant des dômes aplatis ne dépassant pas la demi-sphère.
- Le Dôme de Nagoya (espace multi-fonctionnel, sport et concerts) : Nagoya, Japon, 187,2 m (614 pieds) de large, construit en 1997 par Takenaka Corporation. Coordonnées : 35° 11′ 09,06″ N, 136° 56′ 50,95″ E.
- Tacoma Dome (espace multi-fonctionnel) : Tacoma (État de Washington, États-Unis), 161,5 m (530 pieds) de large, en bois, construit en 1983 par Western Wood. Coordonnées : 47° 14′ 12″ N, 122° 25′ 36,61″ O.
- Superior Dome (Dôme supérieur), Northern Michigan University : Marquette (Michigan, États-Unis), 160 m (525 pieds) de large, dôme en bois construit en 1991 par Western Wood. Coordonnées : 46° 33′ 36,66″ N, 87° 23′ 36,66″ O.
- J. Lawrence Walkup Skydome (Multi-Purpose Arena), Northern Arizona University : Flagstaff (Arizona, États-Unis), 153 m (502 pieds) de diamètre, dôme en bois construit en 1977 construit par Western Wood. Coordonnées : 35° 10′ 50,1″ N, 111° 39′ 10″ O.
- Round Valley Ensphere (stade multi-sports), High School High School : Springerville (Arizona, États-Unis), 134,1 m (440 pieds) de large. Coordonnées : 34° 07′ 13″ N, 109° 17′ 04,91″ O.
- Terminal de Carnival croisières (anciennement Spruce Goose Hangar) : port de Long Beach (Californie, États-Unis), 126,5 m (415 pieds) de diamètre, construit en 1982 par Temcor. Coordonnées : 33° 45′ 04,82″ N, 118° 11′ 19,82″ O.
- Union Tank Car Maintenance Facility : Baton Rouge (Louisiane, États-Unis), 117 m (384 pieds) de large, construit en 1958 par Robert Buckminster Fuller et Synergetics Inc. Coordonnées : 30° 34′ 58,21″ N, 91° 14′ 03,75″ O.
- Lehigh Portland Cement Storage Facility : Union Bridge (Maryland, États-Unis), 114 m (374 pieds) de large, en aluminium, construit en 2001 par Temcor. Coordonnées : 39° 33′ 32,08″ N, 77° 10′ 18,55″ O.
Autres dômes géodésiques remarquables, plus petits mais ayant une forme sphérique.
- La Biosphère de Montréal, dôme géodésique transparent de 80 m de diamètre. Coordonnées : 45° 30′ 50,59″ N, 73° 31′ 53,2″ O.
- Spaceship Earth dans Epcot à Walt Disney World Resort (50 m de diamètre surélevé de 5 m au-dessus du sol) l'une des rares sphères géodésiques construites. Coordonnées : 28° 22′ 31,19″ N, 81° 32′ 57,84″ O.
En France, on peut recenser un certain nombre de dômes géodésiques, en commençant par les plus connus.
- La Géode, Cité des sciences et de l'industrie, à la Villette, 36 m de diamètre, conçue par l'architecte Adrien Fainsilber et construite par l'ingénieur Gérard Chamayou en 1985, et dont les facettes triangulaires, non planes, sont des triangles sphériques réfléchissants ! Coordonnées : 48° 53′ 40,3″ N, 2° 23′ 19,2″ E.
- Le Palais des sports de Paris, 61 m de large, construit en 1959 par Pierre Dufau, à côté du parc des expositions de la porte de Versailles, et rénové en 2002. Coordonnées : 48° 49′ 57,85″ N, 2° 17′ 10,69″ E.
- Le radôme de la station d’écoute (consacrée au renseignement d'origine électromagnétique), à Kourou, en Guyane française.
- La Géode de l'IUT d'Agen, construite par le Cabinet Triangle - Boussac. Coordonnées : 44° 11′ 10,05″ N, 0° 37′ 27,37″ E.
- Le dôme du Laboratoire de Mécanique et Génie Civil à l'Université Montpellier 2 Sciences et Techniques, 10 m de diamètre.
- Un réservoir pétrochimique, construit par Vacono.
Il existe aussi des installations utilisant cette technique ; ainsi l'artiste Michael Pinsky (en) a créé une œuvre d'art intitulée Pollution Pods (en français : Capsules de Pollution) constituée de cinq dômes géodésiques, où l'espace est physiquement clos tout en contenant de l’air pollué de cinq villes du monde[2].
Cinéma
Le film de science-fiction Silent Running sorti en 1972, met en scène une série d'énormes dômes géodésiques en forme de serre attachés à de gros vaisseaux spatiaux servant de cargo qui naviguent autour de l'orbite de Saturne.
Notes et références
- Cet article est partiellement ou en totalité issu de l'article intitulé « Géode (géométrie) » (voir la liste des auteurs).
- Le dôme géodésique en expansion
- « Pollution Pods : quand l’art change notre perception du changement climatique et de la pollution de l’air », sur Veolia Institute (consulté le )
Annexes
Articles connexes
Liens externes
- Ressources relatives aux beaux-arts :
- (en) Grove Art Online
- (en) Museum of Modern Art
- Notice dans un dictionnaire ou une encyclopédie généraliste :



