Courbe de Lissajous

Courbe de Lissajous obtenue sur un oscilloscope.

Une courbe de Lissajous peut toujours être définie par l'équation paramétrique suivante :

${\displaystyle {\begin{cases}x(t)&=a\sin(t+\delta )\\y(t)&=b\sin(nt+\psi )\end{cases}}}$ où ${\displaystyle 0\leq \delta ,\psi \leq {\frac {\pi }{2}}}$ et ${\displaystyle n\geq 1}$.

Le nombre n est appelé le paramètre de la courbe, et correspond au rapport des pulsations des deux mouvements sinusoïdaux. D'ailleurs, si ce rapport est rationnel, il peut être exprimé sous la forme ${\displaystyle n={\tfrac {q}{p}}}$ et l'équation paramétrique de la courbe devient :

${\displaystyle {\begin{cases}x(\theta +\delta )&=a\sin(p\theta )\\y(\theta )&=b\sin(q\theta +\psi )\end{cases}}}$, pour ${\displaystyle 0\leq \theta <2\pi }$ où ${\displaystyle 0\leq \phi \leq {\frac {\pi }{2p}}}$ et ${\displaystyle q\geq p}$.

• Si n est irrationnel, la courbe est dense dans le rectangle [–a, a]×[–b ,b].
• Si n est rationnel,
  • la courbe est une courbe algébrique (unicursale) de degré 2q si ${\displaystyle \phi \in \left]0,{\tfrac {\pi }{2p}}\right]}$ pour p impair ou Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « http://localhost:6011/fr.wikipedia.org/v1/ » :): {\displaystyle \phi\in\left[0,\tfrac\pi{2p}\right[} pour p pair.
  • la courbe est une portion de courbe algébrique de degré q si ${\displaystyle \phi =0}$ pour p impair ou ${\displaystyle \phi ={\tfrac {\pi }{2p}}}$ pour p pair.
• Si n est un entier pair et ${\displaystyle \phi ={\tfrac {\pi }{2}}}$, ou si n est un entier impair et ${\displaystyle \phi =0}$, la courbe est une portion de la courbe du n-ième polynôme de Tchebychev.

• Si n = 1, la courbe est une ellipse.
  • Si a = b et ${\displaystyle \phi ={\frac {\pi }{2}}}$, cette ellipse est un cercle.
  • Si ${\displaystyle \phi =0}$, cette ellipse est un segment de droite.
• Si a = 2b et n = q = 2 (donc p = 1), la courbe est une besace.
  • Si ${\displaystyle \phi ={\frac {\pi }{2}}}$, cette besace est une portion de parabole.
  • Si ${\displaystyle \phi =0}$, cette besace est une lemniscate de Gerono.

Voici quelques exemples de tracés avec ${\displaystyle \phi =0}$ et a = b.

• Différents exemples de courbes de Lissajous
• 
  p = 1, q = 2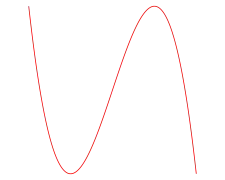
• 
  p = 1, q = 3
• 
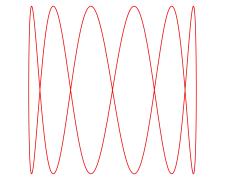  p = 1, q = 6
• 
  p = 2, q = 3
• 
  p = 3, q = 4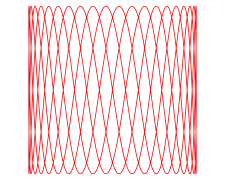
• 
  p = 3, q = 20

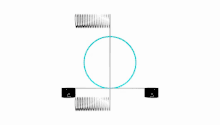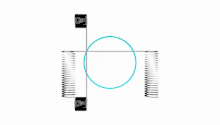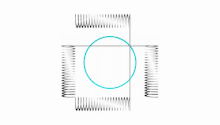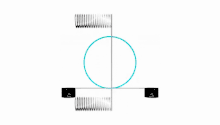
Les courbes de Lissajous sont des projections de couronnes sinusoïdales sur un plan parallèle à l'axe de symétrie.

Traces de lumière en forme de courbe de Lissajous.

Les courbes de Lissajous ont différentes applications :

• Sur un oscilloscope analogique, le mode XY (Abscisse (composante horizontale) et Ordonnée (composante verticale)) permet notamment de mesurer un déphasage et une différence de fréquence entre deux signaux sinusoïdaux par la visualisation de courbes de Lissajous. Cette méthode est néanmoins peu précise.
• Les télescopes spatiaux qui orbitent autour des points de Lagrange, comme notamment le télescope Herschel placé au point L2, décrivent une orbite de Lissajous.