AccueilđŸ‡«đŸ‡·Chercher

Clapotis (hydrodynamique)

En hydrodynamique, le clapotis est une forme d'ondes stationnaires non-dĂ©ferlantes provoquĂ©e entre autres par la rĂ©flexion d'un train d'ondes de surface sur un rivage presque vertical tel un brise-lames, une digue ou une falaise abrupte[1] - [2] - [3] - [4]. L'onde clapotique rĂ©sultante ne se dĂ©place pas horizontalement et sa structure de nƓuds et de ventres est fixe[5] - [6]. Ces vagues favorisent l'Ă©rosion au pied de la paroi [7] et peuvent gravement endommager les structures sur le rivage[8]. Le terme a Ă©tĂ© inventĂ© en 1877 par le mathĂ©maticien et physicien français Joseph Valentin Boussinesq[9] - [10].

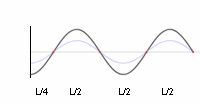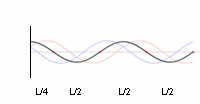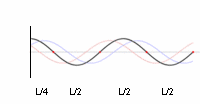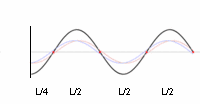
L'onde incidente (en rouge) réfléchie sur la paroi produit l'onde réfléchie (en bleu). La superposition des deux produit le clapotis (en noir).

Dans le cas idĂ©al de "clapotis complet" oĂč une onde incidente purement monotone est complĂštement rĂ©flĂ©chie normalement Ă  une paroi verticale solide[11] - [12], la hauteur des ondes stationnaires est le double de la hauteur des ondes incidentes Ă  une distance d'une demi-longueur d'onde de la paroi[13]. Dans ce cas, les orbites circulaires des particules d'eau dans l'onde d'eau profonde sont converties en un mouvement purement linĂ©aire, avec des vitesses verticales aux ventres et des vitesses horizontales aux nƓuds[14]. Les ondes stationnaires montent et descendent alternativement de façon symĂ©trique, Ă  mesure que l'Ă©nergie cinĂ©tique est convertie en Ă©nergie potentielle, et vice versa[15].

PhénomÚnes associés

Le clapotis vĂ©ritable est trĂšs rare, car la profondeur de l'eau ou l'escarpement du rivage sont peu susceptibles de satisfaire complĂštement aux exigences idĂ©alisĂ©es[15]. Dans le cas plus rĂ©aliste des clapotis partiels, oĂč une partie de l'Ă©nergie des vagues incidentes est dissipĂ©e sur le rivage[16], l'onde incidente est rĂ©flĂ©chie Ă  moins de 100%[11] et une onde stationnaire seulement partielle se forme lĂ  oĂč les mouvements de la particule d'eau sont elliptiques[17]. Cela peut Ă©galement se produire en mer entre deux trains d'ondes de longueur d'onde presque Ă©gale, mais avec des amplitudes inĂ©gales, lorsque les deux trains d'ondes se dĂ©placent dans des directions opposĂ©es. Dans le clapotis partiel, l'enveloppe de l'onde prĂ©sente un mouvement vertical aux nƓuds.

Lorsqu'un train d'ondes heurte un mur obliquement, le train d'ondes rĂ©flĂ©chi repart Ă  l'angle supplĂ©mentaire, crĂ©ant un motif d'interfĂ©rence d'ondes hachurĂ©es connu sous le nom de clapotis gaufrĂ©[8]. Dans cette situation, les crĂȘtes individuelles formĂ©es Ă  l'intersection des crĂȘtes des trains d'ondes incidentes et rĂ©flĂ©chies se dĂ©placent parallĂšlement Ă  la structure. Ce mouvement ondulatoire, lorsque combinĂ© avec les tourbillons qui en rĂ©sultent, peut Ă©roder le matĂ©riau des fonds marins et le transporter le long du mur, sapant la structure jusqu'Ă  ce qu'elle se brise.

Les ondes clapotiques à la surface de la mer font également rayonner des microbaroms infra-soniques dans l'atmosphÚre et des signaux sismiques appelés microséismes couplés à la Terre solide à travers le plancher océanique[18].

Le clapotis est aussi considéré comme un fléau et un plaisir du kayak de mer[19].

Voir Ă©galement

Références
  1. « clapotis », Glossary of Meteorology, American Meteorological Society (consulté le )
  2. « clapotis », Glossary of Scientific Terms, University of Alberta (consulté le )
  3. Eid et Zemell, « Dynamic analysis of a suspended pump in a vertical well connected to the ocean », Canadian Journal of Civil Engineering, vol. 10, no 3,‎ , p. 481–491 (DOI 10.1139/l83-075) :
    « The standing wave system resulting from the reflection of a progressive wave train from a vertical wall (clapotis)
 »
    Eid et Zemell, « Erratum: Dynamic analysis of a suspended pump in a vertical well connected to the ocean », Canadian Journal of Civil Engineering, vol. 11,‎ , p. 137 (DOI 10.1139/l84-025)
  4. prepared by the Task Committee on Hydrology Handbook of Management Group D of the American Society of Civil Engineers., Hydrology handbook, New York, ASCE, (ISBN 978-0-7844-0138-5) :
    « This simplification assumes that a standing wave pattern, called clapotis, forms in front of a wall where incident and reflected waves combine. »
  5. Carter, Bill, Coastal environments: an introduction to the physical, ecological, and cultural systems of coastlines, Boston, Academic Press, (ISBN 978-0-12-161856-8), p. 50 :
    « 
if the wave travels in exactly the opposite direction then a standing, or clapotic, wave can develop. »
  6. Matzner, Richard A., Dictionary of geophysics, astrophysics, and astronomy, (ISBN 978-0-8493-2891-6, Bibcode 2001dgaa.book.....M, lire en ligne), p. 81 :
    « clapotis
denotes a complete standing wave — a wave which does not travel horizontally but instead has distinct nodes and antinodes. »
  7. Beer, Tom, Environmental oceanography, Boca Raton, CRC Press, (ISBN 978-0-8493-8425-7), p. 44 :
    « ... the reflected wave energy interacted with the incoming waves to produce standing waves known as clapotis, which promote erosion at the toe of the wall. »
  8. Fleming, Christopher, Reeve, Dominic et Chadwick, Andrew, Coastal engineering: processes, theory and design practice, London, Spon Press, , 47 p. (ISBN 978-0-415-26841-7) :
    « Clapotis Gaufre When the incident wave is at an angle α to the normal from a vertical boundary, then the reflected wave will be in a direction α on the opposite side of the normal. »
  9. Iooss, G., « J. Boussinesq and the standing water waves problem », Comptes Rendus MĂ©canique, vol. 335, nos 9–10,‎ , p. 584–589 (DOI 10.1016/j.crme.2006.11.007, Bibcode 2007CRMec.335..584I, lire en ligne, consultĂ© le ) :
    « In this short Note we present the original Boussinesq's contribution to the nonlinear theory of the two dimensional standing gravity water wave problem, which he defined as ‘le clapotis’. »
  10. Iooss, Plotnikov et Toland, « Standing Waves on an Infinitely Deep Perfect Fluid Under Gravity », Archive for Rational Mechanics and Analysis, vol. 177, no 3,‎ , p. 367–478 (DOI 10.1007/s00205-005-0381-6, Bibcode 2005ArRMA.177..367I, lire en ligne [archive du ], consultĂ© le ) :
    « It was, we believe, Boussinesq in 1877 who was the first to deal with nonlinear standing waves. On pages 332-335 and 348-353 of[7]he refers to ‘le clapotis’, meaning standing waves, and his treatment, which includes the cases of finite and infinite depth, is a nonlinear theory taken to second order in the amplitude. »
  11. Guidelines and Specifications for Flood Hazard Mapping Partners, Federal Emergency Management Agency, , « D.4.14 Glossary » :
    « CLAPOTIS The French equivalent for a type of STANDING WAVE. In American usage it is usually associated with the standing wave phenomenon caused by the reflection of a nonbreaking wave train from a structure with a face that is vertical or nearly vertical. Full clapotis is one with 100 percent reflection of the incident wave; partial clapotis is one with less than 100 percent reflection. »
  12. Mai, S., Paesler, C. et Zimmermann, C., « Wellen und Seegang an KĂŒsten und KĂŒstenbauwerken mit Seegangsatlas der Deutschen NordseekĂŒste : 2. Seegangstransformation (Waves and Sea State on Coasts and Coastal Structures with Sea State Atlas of the German North Sea Coast : 2. Sea State Transformation) », UniversitĂ€t Hannover, UniversitĂ€t Hannover,‎ (lire en ligne [PDF], consultĂ© le ) :
    « Ein typischer extremer Fall von Reflektion tritt an einer starren senkrechten Wand auf. (A typical case of extreme reflection occurs on a rigid vertical wall.) »
  13. Jr, Ben H. Nunnally, Construction of Marine and Offshore Structures, Third Edition, Boca Raton, Florida, CRC Press, (ISBN 978-0-8493-3052-0), p. 31 :
    « Waves impacting against the vertical wall of a caisson or against the side of a barge are fully reflected, forming a standing wave or clapotis, almost twice the significant wave height, at a distance from the wall of one-half wavelength. »
  14. van Os, Magchiel, Breaker Model for Coastal Structures : Probability of Wave Impacts on Vertical Walls, Technische Universiteit Delft, Hydraulic and Offshore Engineering division, , 4–33 p., « 4.2 Pressures due to Non-Breaking Waves » :
    « This phenomenon is also called "Clapotis" and the circular orbits of the particle movements have degenerated into straight lines. This results in only vertical velocities at the antinodes and horizontal velocities at the nodes. »
  15. Woodroffe, C. D., Coasts: form, process, and evolution, Cambridge, UK, Cambridge University Press, (ISBN 978-0-521-01183-9), p. 174 :
    « The standing wave will alternately rise and collapse as kinetic energy is converted into potential energy and back again. »
  16. Hirayama, K., « Numerical Simulation of Nonlinear Partial Standing Waves using the Boussinesq Model with New Reflection Boundary », Report Ff the Port and Airport Research Institute, vol. 40, no 4,‎ , p. 3–48 :
    « The waves in front of actual seawalls and harbor breakwaters, however, are rather partial standing waves such that some incident wave energy is dissipated
 »
  17. Leo H. Holthuijsen, Waves in Oceanic and Coastal Waters, Cambridge, UK, Cambridge University Press, (ISBN 978-0-521-86028-4), p. 224 :
    « A partially standing wave due to the (partial) reflection of an incident wave against an obstacle. The ellipses are the trajectories of the water particles as they undergo their motion in one wave period. »
  18. Tabulevich, Ponomarev, Sorokin et Drennova, « Standing Sea Waves, Microseisms, and Infrasound », Izv. Akad. Nauk, Fiz. Atmos. Okeana, vol. 37,‎ , p. 235–244 (lire en ligne, consultĂ© le ) :
    « In this process, the interference of differently directed waves occurs, which forms standing water waves, or the so-called clapotis.
To examine and locate these waves, it is proposed to use their inherent properties to exert (“pump”) a varying pressure on the ocean bottom, which generates microseismic vibrations, and to radiate infrasound into the atmosphere. »
  19. « Clapotis », (consulté le )

Lectures complémentaires
  • Boussinesq, « ThĂ©orie des ondes liquides pĂ©riodiques », MĂ©moires PrĂ©sentĂ©s Par Divers Savants Ă  l'AcadĂ©mie des Sciences, vol. 20,‎ , p. 509–616
  • Boussinesq, « Essai sur la thĂ©orie des eaux courantes », MĂ©moires PrĂ©sentĂ©s Par Divers Savants Ă  l'AcadĂ©mie des Sciences, vol. 23, no 1,‎ , p. 1–660
  • Hires, « Étude du clapotis », La Houille Blanche, vol. 15, no 2,‎ , p. 153–63 (DOI 10.1051/lhb/1960032)
  • B. LemĂ©hautĂ© et J. I. Collins, Clapotis and Wave Reflection: With an Application to Vertical Breakwater Design, Civil Engineering Dept., Queen's University at Kingston, Ontario,

Liens externes
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplĂ©mentaires peuvent s’appliquer aux fichiers multimĂ©dias.