Circuit équivalent de Mason
Le circuit équivalent de Mason est utilisé dans la simulation de transducteurs piézoélectriques. Il doit son nom à Warren P. Mason, des Laboratoires Bell, qui l'a publié dans les années 1940[1]. L'autre schéma utilisé est le circuit équivalent de KLM. Dans l'un et l'autre, le fonctionnement mécanique du transducteur est simplifié à une seule dimension. Le modèle, utilisant l'Analogie électro-mécanique, décrit le comportement d'une couche piézoélectrique utilisée dans son mode épaisseur (c'est-à-dire que le vecteur polarisation et le champ électrique sont orientés selon sa petit dimension) sous la forme d'un circuit présentant trois ports : un port électrique, deux ports mécaniques correspondant aux grandeurs mécaniques (force et vitesses) sur les deux faces.
Schéma d'une couche piézoélectrique
Le schéma prend la forme suivante. Les notations ne sont uniformes selon les auteurs, on utilise ici celles de Sheritt en 1999[2] :
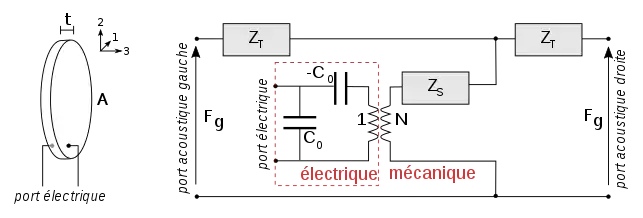
Les termes utilisés dans le schéma sont les suivants :
- la capacité : ;
- l'impédance mécanique :
- la conversion électromécanique, représentée comme un transformateur, a un coefficient de conversion : ;
- le nombre d'onde , avec la fréquence angulaire ;
- ;
- ;
Le tout pour une couche piézoélectrique de surface et d'épaisseur .
Ces définitions font appel aux propriétés piézoélectriques du matériau considéré :
- la masse volumique du matériau : (en kg m−3) ;
- la rigidité du matériau dans l'axe 3 : (en N m−2) ;
- la permittivité relative à déformation constante : (adimensionnelle) ;
- la constante piézoélectrique : (en V/m).
Par convention, l'axe 3 est la direction de polarisation du matériau. Notons qu'en l'absence de pertes, et divergent pour , c'est-à-dire lors de la résonance en .
Terminaison des ports mécaniques
Les terminaisons à gauche et à droite du schéma ci-dessus représentent, par le biais de l'analogie électro-mécanique, la situation sur les deux faces du matériau piézoélectrique. Ainsi, des couches situées sur une face ou l'autre vont être représentées par des guides d'ondes mécaniques. Un milieu semi-infini est représenté en terminant le port correspondant par une impédance acoustique .
Si l'une des face est dans le vide (c'est-à-dire que l'impédance acoustique du milieu est négligeable), le port correspondance est fermé par un court-circuit : un court-circuit impose en effet une tension nulle, donc, dans le cas de l'analogie électromécanique, une contrainte nulle.
Ainsi on peut calculer l'impédance électrique de la plaque piézoélectrique seule (deux faces libres) : ,
où le symbole dénote l'assemblage en parallèle de deux impédances, c'est-à-dire .
Après remplacement des termes par leurs expressions respective et simplification, on obtient : .
Cette expression est notamment utile pour déterminer les propriétés piézoélectriques du matériau par problème inverse, l'impédance électrique étant facile à mesurer expérimentalement[3].
Utilisation et limites
Le présence d'une capacité négative a souvent été perçue comme une limite du modèle, étant jugée contre-instinctive et « non physique »[2]. Le modèle de Mason est très utilisé comme modèle simple du comportement d'une couche piézoélectrique, permettant de fournir un dimensionnement rapide. Il présente cependant les limites dues à sa simplicité : tout effet latéral dans le plan est ignoré (condition aux limites latéral, modes de vibration dans le plan), toutes les propriétés sont supposées homogènes.
Références
- (en) Warren P. Mason, Electromechanical Transducers and Wave Filters, Van Nostrand Reinhold Inc.,U.S, (ISBN 0442051646)
- S. Sherrit, S.P. Leary, B.P. Dolgin et Y. Bar-Cohen, « Comparison of the Mason and KLM equivalent circuits for piezoelectric resonators in the thickness mode », 1999 IEEE Ultrasonics Symposium. Proceedings. International Symposium (Cat. No.99CH37027), IEEE, vol. 2, , p. 921–926 (ISBN 9780780357228, DOI 10.1109/ULTSYM.1999.849139, lire en ligne, consulté le )
- (en) « 176-1987 », IEEE standards, (DOI 10.1109/ieeestd.1988.79638, lire en ligne, consulté le )





















