Choix intertemporel
Un choix intertemporel est un choix qui implique des évènements situés à des moments différents. L'étude des choix intertemporels consiste à déterminer dans quelle mesure les individus accordent une préférence au futur proche par rapport à un futur plus lointain, et à décrire les mécanismes psychologiques et cérébraux à l'œuvre.
On peut montrer que pour qu'un individu effectue des choix stables au cours du temps, il faudrait que ses préférences soient une fonction exponentielle décroissante du temps, et cette analyse a été largement reprise en économie. Cependant les études empiriques constatent que les choix humains suivent d'autres lois et notamment que les choix comportant une récompense immédiate ne sont pas évalués de la même façon que les choix n'impliquant que des événements futurs[1]. Il semble que cela s'explique par l'activation de circuits cérébraux distincts pour les récompenses immédiates[2].
Le modèle de Fisher
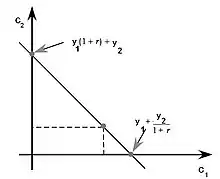
Le modèle de Fisher peut être illustré en prenant deux périodes : la période actuelle ou période 1 (ce mois ou cette année) et la période future ou période 2 (le mois prochain ou l’année prochaine). L’individu planifie sa consommation compte tenu de ses besoins et de ses revenus attendus. Sa contrainte budgétaire est :
où est la consommation présente et la consommation future; le revenu présent et le revenu futur. La somme épargnée (si cette différence est positive) ou empruntée (si cette différence est négative) est placée ou empruntée au taux d’intérêt . Le consommateur maximise ses préférences représentées par la fonction d’utilité intertemporelle . En prenant le Lagrangien :
où est une variable auxiliaire (le multiplicateur), on obtient les conditions de premier ordre suivantes :
En résolvant ce système d’équations on obtient les fonctions de consommation:
Des conditions de premier ordre on tire la relation suivante:
Le terme à gauche est appelé le taux de préférence pour le temps. À l’équilibre, il doit être égal au taux d’intérêt[3].
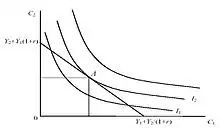
Graphiquement, la solution est obtenue lorsque la courbe d’indifférence la plus élevée est tangente à la droite représentant la contrainte budgétaire (point A).
Variation du taux d’intérêt
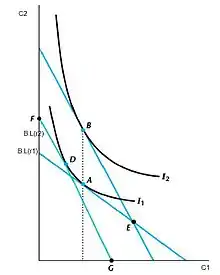
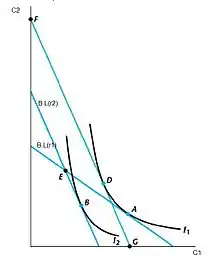
Si le taux d’intérêt augmente, la droite budgétaire subit une rotation en sens horaire avec comme pivot le point où la consommation de chaque période correspond au revenu de la période.
Cette variation a un effet de revenu (le consommateur qui a épargné en période 1 aura un revenu plus élevé en période 2) et un effet de substitution (il devient plus intéressant d’épargner car l’épargne rapporte davantage)[4]. Si l’individu voulait emprunter, l’effet total est une baisse de la consommation en période 1. Par contre, en cas d’épargne le résultat final est ambigu.
En utilisant la théorie de la préférence révélée on peut dire qu’un consommateur qui épargne reste toujours un prêteur en cas de hausse du taux d’intérêt. Si le taux baisse, c’est l’individu emprunteur qui reste toujours un débiteur en période 1[5].
Tous ces résultats ne sont plus valables s’il y a plus de deux périodes. En effet, on ne doit pas nécessairement rembourser la période suivante ce qu’on a emprunté.
La règle de Keynes-Ramsey
On fait souvent l’hypothèse que la fonction d’utilité intertemporelle est de forme additive dans les périodes. On a alors :
où est le ``taux subjectif d’escompte’’ du temps et l’utilité instantanée. L’idée que les individus ``escomptent’’ les utilités futures comme avec les valeurs financières remonte à Böhm-Bawerk. Selon cet auteur[6] la sous-estimation des biens futurs est due à un manque d’imagination et à une faiblesse de volonté des individus.
En remplaçant par la valeur tirée de la contrainte budgétaire, on obtient la condition de premier ordre suivante pour la maximisation de la fonction d’utilité intertemporelle:
En prenant cette équation intertemporelle de Euler on obtient la règle de Keynes-Ramsey[7]:
Le taux marginal de substitution intertemporel doit être égal au prix relatif des consommations.
Généralisation en temps continu
Lorsqu’on prend de nombreuses périodes, on préfère travailler en temps continu. La fonction d’utilité intertemporelle est alors :
L’évolution de la consommation dépend de l’équation différentielle:
où sont les actifs financiers, le revenu non financier, la consommation et le point au-dessus de la variable désigne la dérivée par rapport au temps. Comme les valeurs financières futures ne peuvent pas avoir une valeur actuelle négative, il faut imposer la restriction:
(pas de chaîne de Ponzi)
En utilisant la méthode de Pontryagin on a la valeur courante de l’hamiltonien:
où est la costate (une variable auxiliaire). Après avoir remplacé cette variable dans les conditions de premier ordre[8] - [9] on trouve la règle de Keynes-Ramsey:
où:
Le taux de croissance optimal de la consommation dépend de l’élasticité de substitution intertemporelle et de l’excès du taux d’intérêt par rapport au taux subjectif d’escompte du temps.
Escompte hyperbolique
Des expériences effectuées avec des étudiants montrent que la sous-estimation des biens futurs ne suit pas une loi exponentielle. Par exemple, Thaler[10] a observé qu’en moyenne les individus demandaient, plutôt que d’avoir 15 $ immédiatement, 20 $ un mois après, 50 $ une année après et 100 $ 10 ans après. Ces valeurs impliquent un taux de 400% pour un mois, 233.33% pour une année et 20.089% pour dix ans. Une diminution du taux avec l’éloignement du temps peut être représentée avec une loi hyperbolique:
Lorsque tend vers 0 on retrouve l’escompte exponentiel: .
Un escompte hyperbolique conduit à une incohérence temporelle[11]. Même si rien ne change, le consommateur ne va pas suivre le plan de consommation qu’il avait envisagé précédemment.
Modèle du cycle de vie de Modigliani
Le point de départ de la théorie du cycle de vie est le modèle de Fisher avec un horizon temporel égal à toute la vie du consommateur. Supposons que le revenu annuel soit constant et égal à jusqu’à l’âge de la retraite et nul après. Si le consommateur vit ans, la consommation uniforme sera de (on suppose que le taux d’intérêt soit nul). Le consommateur épargne chaque année , jusqu’à l’âge de la retraite, et ensuite il utilisera l’épargne accumulée pour consommer pendant les années de retraite.
Dans le cas plus général[12], soit la valeur présente des revenus attendus par l’individu d’âge T en l’année t:
où est le capital accumulé, les revenus attendus et r te taux d’intérêt.
Si la fonction d’utilité est homogène par rapport aux consommations, on obtient la fonction de consommation suivante:
où est le revenu attendu moyen et un facteur proportionnel dépendant de la fonction d’utilité.
On peut généraliser le modèle en introduisant l’épargne pour des buts d’héritage, la sécurité sociale ou une durée de vie incertaine.
La théorie de Modigliani est utilisée pour étudier les systèmes de retraite publics et privés et le lien entre épargne et croissance[13].
Le modèle de Friedman
Selon Friedman[14], la consommation dépend du revenu permanent de l’individu, c’est-à-dire le revenu moyen à long terme :
où est la consommation (permanente), le revenu permanent et est un coefficient qui dépend du taux d’intérêt, du taux de préférence pour le temps et du rapport entre la fortune du consommateur et son revenu.
Soit la consommation de l’individu i au temps t. On a:
où est la consommation transitoire. D’autre part:
Le revenu transitoire n’a pas d’effet sur la consommation globale.
Friedman suppose qu’il n’y a pas de corrélation entre certaines de ces variables, en particulier entre le revenu transitoire et la consommation transitoire:
où désigne le coefficient de corrélation.
Friedman propose d’estimer le revenu permanent par la technique des retards échelonnés:
où sont des coefficients.
Les estimations avec des données agrégées montrent que la variation de la consommation par rapport à une variation du revenu est plus importante que celle prévue par la théorie du revenu permanent (variation excessive)[15].
Les estimations avec des données individuelles donnent des résultats assez favorables à la théorie du revenu permanent et à celle de la théorie du cycle de vie [16].
Notes
Références
- (en) Frederick et Loewenstein, « Time discounting and time preference: A critical review », Journal of economic literature, .
- (en) Samuel M. McClure, David I. Laibson, George Loewenstein, Jonathan D. Cohen, « Separate Neural Systems Value Immediate and Delayed Monetary Rewards », Science, no 5694, (DOI 10.1126/science.1100907).
- (en) Fisher Irving, The Theory of Interest, New York, 1907, p. 291.
- (en) J.M. Henderson and R.E. Quandt, Microeconomic Theory, London, 1980, p. 331.
- Hal R. Varian, Introduction à la microéconomie, Bruxelles, 2000, p. 198
- Eugen von Böhm-Bawerk, Kapital und Kapitalzins, Insbruck, 1914
- Frank Ramsey, « A Mathematical Theory of Saving », Economic Journal, 1928, p. 543-559
-
- La condition de transversalité doit aussi être satisfaite:
- Richard Thaler, « Some empirical evidence on dynamic inconsistency «, Economic Letters, 1981, p. 201-207
- Robert Strotz, « Myopia and Inconsistency in Dynamic Utility Maximisation «, Review of Economic Studies, 1956, p. 165-180
- Francesco Franco Modèle:Et. al., The Collected Papers of Franco Modigliani, vol. 6, Boston, 2005, p. 49
- Angus Deaton, « Franco Modigliani and the life-cycle theory of consumption », .BNL Quarterly Review, 2005, p. 91-107
- Milton Friedman, A Theory of the Consumption Function, Princeton, 1957.
- John Campbell and Gregory Mankiw, « Permanent Income, Current Income, and Consumption », Journal of Business and Economic Statistics, 1990, p. 265-279
- Orazio Attanasio and Martin Browning, « Testing the Life Cycle Model of Consumption: what can we learn from micro and macro data », Investigaciones Economicas, 1994, p. 433-463
voir aussi
Bibliographie
- (en) Olivier Blanchard et Stanley Fischer, Lectures on Macroeconomics, Boston, 1989
- (en) Gernot Doppelhofer, « Intertemporal Macroeconomics », N.F.G. Allington et J.S.L. McCombie, Cambridge Essays in Applied Economics, Cambridge, 2003
- (en) Rudiger Dornbusch et Stanley Fischer, Macro-Economics, London, 1981
- Hal R. Varian, Introduction à la microéconomie, Bruxelles, 2000








![{\displaystyle L=V(C_{1},C_{2})+\lambda \left[Y_{1}(1+r)+Y_{2}-C_{1}(1+r)-C_{2}\right]}](https://img.franco.wiki/i/d4ced5bc2f866594cbafea3db029f6d12c550b72.svg)

















![{\displaystyle {\mathcal {H}}^{c}=u(C_{t})+\lambda \left[rA+Y-C\right]}](https://img.franco.wiki/i/7e5a10ee27b7b1e9cfc5249532eaa57b9c8c1cfb.svg)


![{\displaystyle \left[1/\theta (C)\right]}](https://img.franco.wiki/i/2350e74d615a4bdb9eabd796470c57af16d2eff1.svg)






![{\displaystyle \left[{\frac {N}{L}}{\bar {Y}}\right]}](https://img.franco.wiki/i/db9aed8ea816ba932611a3a2366a2d26e96500bd.svg)




















![{\displaystyle {\dot {\lambda }}=\rho \lambda -{\frac {\partial {\mathcal {H}}^{c}}{\partial A}}=\lambda \left[\rho -r\right]}](https://img.franco.wiki/i/60369195aeee73393f840f6063b21104f34ec678.svg)
