Carré logique
Le carré logique ci contre représente les oppositions logiques entre les quatre propositions :
- Proposition notée A, universelle affirmative : « tous les S sont P » (SaP : S are all P)
- Proposition notée E, universelle négative : « aucun S n'est P » ou « tous les S sont non-P » (SeP : S excluded from P)
- Proposition notée I, particulière affirmative : « au moins un S est P » (SiP : some S in P).
- Proposition notée O, particulière négative : « au moins un S est non-P » (SoP : some S out of P), qui exprime la précédente négativement.
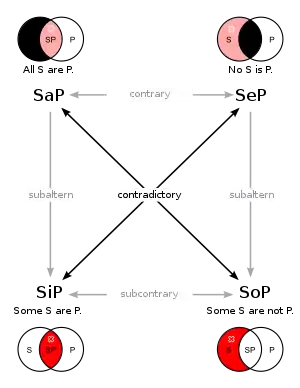
Le carré logique
Forme classique
Deux propositions disposant des mêmes sujets S et prédicat P peuvent s'opposer par leur qualité (P ou non-P) et/ou par leur quantité de sujets. Ainsi les oppositions qui peuvent être créées sont les suivantes :
- Deux propositions contradictoires sont des propositions qui s'opposent par la qualité et la quantité. L'une est vraie si et seulement si l'autre est fausse.
- Deux propositions contraires sont des propositions universelles qui s'opposent par la qualité. Les deux propositions peuvent être fausses en même temps, mais pas vraies en même temps.
- Deux propositions subcontraires sont des propositions particulières qui s'opposent par la qualité. Les deux propositions peuvent être vraies en même temps, mais pas fausses en même temps.
- Deux propositions subalternes sont des propositions qui s'opposent par la quantité. Si la proposition universelle est vraie, alors la proposition particulière est vraie aussi.
On établit ainsi le carré logique de l'opposition des propositions.
| A : Tous les S sont P | ←Contraire→ | E : Aucun S n’est P |
| ↕Subalterne↕ | Contradictoire | ↕Subalterne↕ |
| I : Au moins un S est P | ←Subcontraire→ | O : Au moins un S est non-P |
Autres carrés
Créé au IIe siècle après J-C[1], le carré logique présente une telle régularité que l'on a essayé, à l'époque moderne, de l'appliquer à plusieurs domaines formalisés :
- en sémiotique, le carré sémiotique a été développé par Greimas ;
- en logique modale, M. et W. Kneale[2] ont présenté le carré logique des modalités selon Diodore :
| nécessaire (vrai, jamais faux) | ←Contraire→ | impossible (faux, jamais vrai) |
| ↕Subalterne↕ | Contradictoire | ↕Subalterne↕ |
| possible (parfois vrai) | ←Subcontraire→ | non nécessaire (parfois faux) |
- en logique épistémique, on a également pu se demander, à l'instar de Pascal Engel[3], si l'on peut concevoir un carré épistémique ;
- en sémantique argumentative, plus précisément, dans le cadre de la Théorie des blocs sémantiques[4], Marion Carel et Oswald Ducrot proposent un "carré argumentatif", inspiré du carré d'Aristote, reliant par des propriétés formelles des « prédicats argumentatifs » (dans leur terminologie, des "aspects argumentatifs") en « donc » et en "pourtant".
Références
- Juliette Lemaire, « La contradiction dans l'Organon d’Aristote », L’enseignement philosophique, vol. 58e Année, no 3, , p. 3–21 (ISSN 0986-1653, DOI 10.3917/eph.583.0003, lire en ligne, consulté le )
- The Development of logic, Oxford, Clarendon Press, 1962, p. 125. Reproduit par Jules Vuillemin dans Nécessité ou contingence, Paris, Minuit, 1984, p. 78, note 33.
- « À quoi ressemblerait le carré logique épistémique ? », The Square of Opposition, International Congress, Montreux, 2 juin 2007.
- cf.Marion Carel et Oswald Ducrot (1999) « Le problème du paradoxe dans une sémantique argumentative », Langue française no 123 : 6-26. Marion Carel (2005) « La construction du sens des énoncés », Revue romane, no 40-41, p. 79-97. Voir également Kohei Kida (1998) Une sémantique non véritative des énoncés conditionnels : essai de traitement argumentatif, thèse de doctorat (EHESS), p. 262-277.
Voir aussi
Bibliographie
- Robert Blanché, Sur le système des connecteurs interpropositionnels, Cahier pour l'analyse, vol. 10 : "La formalisation", 1969. Texte en ligne. Concernant le carré et l'hexagone logique.
- Robert Blanché, Structures intellectuelles (1966). Robert Blanché est mort en 1975. Neuf ans avant sa mort, en 1966, il publia chez Vrin un ouvrage important:Structures intellectuelles. Il y parle de l'hexagone logique qui comportant six postes est une figure plus puissante que le carré logique traditionnel qui en comporte quatre seulement.
- hexagone logique dans wikipedia francophone et dans le Dictionnaire encyclopédique des sciences du langage, édité par le Seuil. L'hexagone logique de Robert Blanché ajoute les valeurs Y et U aux quatre valeurs du carré. Dans Structures intellectuelles, Y est la conjonction de I et de O, U la disjonction exclusive de A et de E.
Articles connexes
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.