Bernard Morin
Bernard Morin est un mathématicien français né le à Shanghai et mort le dans le 14e arrondissement de Paris[1] - [2]. Il était aveugle depuis l'âge de six ans à cause d'un glaucome, mais sa cécité ne l'a pas empêché de mener une carrière en mathématiques.
| Naissance | |
|---|---|
| Décès |
(Ă 87 ans) 14e arrondissement de Paris |
| Nom de naissance |
Bernard Carlo Gabriel Morin |
| Nationalité | |
| Formation | |
| Activité |
| A travaillé pour |
|---|
Il a été membre du groupe qui a le premier montré[3] le retournement de la sphère, c'est-à -dire l'homotopie qui commence avec une sphère et qui termine avec la même sphère retournée (faces interne et externe échangées). Il a aussi découvert la surface de Morin, qui est une étape pour le retournement de la sphère, qu'il utilise pour trouver une borne inférieure au nombre d'étapes nécessaires pour retourner la sphère.
Il a découvert la première paramétrisation de la surface de Boy en 1978.
Son étudiant de thèse François Apéry a découvert plus tard (en 1986) une autre paramétrisation de la surface de Boy qui est conforme à la méthode générale de paramétrisation de surfaces non orientables[4].
Morin a travaillé à l'Institute for Advanced Study à Princeton. Il a passé la plus grande partie de sa carrière à l'université de Strasbourg.
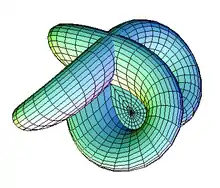Surface de Morin
Coupe animée de la surface de Boy
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bernard Morin » (voir la liste des auteurs).
- « Décès de Bernard Morin - Société Mathématique de France » (consulté le )
- Lieux de naissance et décès trouvés dans la base MatchId des fichiers de décès en ligne du Ministère de l'Intérieur avec les données INSEE (consultation 4 janvier 2020)
- Bernard Morin, « Équations du retournement de la sphère », C. R. Acad. Sc. Paris, a, t. 287,‎ , p. 879-882 (Dans cette Note on donne les équations d'une suite de familles continues à un paramètre d'immersions de la sphère qui relient le plongement standard au plongement antipodal, ainsi qu'une paramétrisation de la surface de Boy., lire en ligne, consulté le ).
- (en) Eric W. Weisstein, « Boy Surface », sur MathWorld.
Bibliographie
- (en) George K. Francis et Bernard Morin, « Arnold Shapiro’s Eversion of the Sphere », The Mathematical Intelligencer, vol. 2, no 4,‎ , p. 200-203
Liens externes
- (en) « Photos from the Maubeuge symposium "Arts et Mathématiques" » : Morin avec des modèles stéréolithographiques du retournement de la sphère
- (en) « The World of Blind Mathematicians » [PDF], sur AMS