Automate fini inambigu
En théorie des automates, un automate fini inambigu (on dit aussi non ambigu, en anglais « unambiguous finite automaton », abrégé en UFA) est un automate fini non déterministe d'un type particulier. C'est un automate qui, pour chaque mot accepté, ne possède qu'un seul calcul réussi. Tout automate fini déterministe est inambigu, mais la réciproque est fausse. Les trois types d'automates : non déterministe, inambigu, déterministe, reconnaissent les mêmes langages formels, à savoir les langages réguliers.
Le nombre d'états d'un automate inambigu peut être exponentiellement plus petit qu'un automate déterministe équivalent. En contre-partie, certains problèmes sont plus difficiles à résoudre pour les automates inambigus que pour les automates déterministes. Par exemple, partant d'un automate A, un automate A' reconnaissant le complément du langage accepté par A se construit en temps linéaire si A est déterministe, mais il a été démontré qu'il ne peut être calculé en temps polynomial si A est inambigu[1].
La notion d'automate inambigu se généralise à d'autres modèles de machines ou de calcul. Un présentation générale a été donnée par Thomas Colcombet[2].
Définition
Un automate fini non déterministe , où est l'ensemble des transitions, l’ensemble des états initiaux et l'ensemble des états terminaux, est dit inambigu si, pour tout mot reconnu par l'automate, il existe un seul chemin réussi d'étiquette , donc un seul chemin
- , avec et .
Exemple
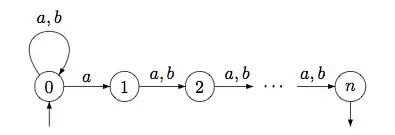
Soit l'ensemble des mots sur l'alphabet binaire dont la lettre en position depuis la fin est un . Les figures ci-contre montrent un automate inambigu reconnaissant ce langage pour n=2, et un automate déterministe pour ce même langage.
*a(a%252Bb)%5E2.svg.png.webp)
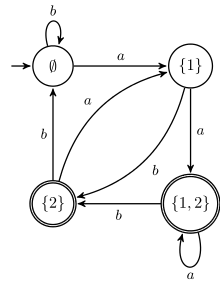
L'automate déterministe minimal acceptant a états, alors que l’automate inambigu pour le même langage n'a que états.
Propriétés
Test d'ambiguïté
On peut tester si un automate fini non déterministe à m transitions est inambigu en temps . On peut même calculer le degré d’ambiguïté, et savoir si l'ambiguïté est bornée, si elle croit polynomialement ou exponentiellement avec la longueur des mots[3].
Inclusion
Le problème d'inclusion consiste à tester si le langage reconnu par un automate est contenu dans le langage reconnu par un automate . Le problème est bien entendu décidable. La question est celle de sa complexité.
Le problème de l'inclusion pour les automates inambigus est décidable en temps polynomial : il est dans la classe PTIME alors que ce même problème est PSPACE-complet pour les automates non déterministes[4] - [5]. C'est d'ailleurs ce problème, décrit par Meyer et Stockmeyer en 1972[6] qui est le premier problème de cette classe.
La démonstration de cette propriété utilise le fait que le produit cartésien de deux automates inambigus est également inambigu[4].
Soient et deux automates, et et les langages acceptés. On a si et seulement si , où désigne l'automate produit reconnaissant . Les deux ensembles et sont égaux si et seulement si le nombre de mots de longueur dans et égal au nombre de mots de longueur dans pour tout . Comme ces suites de nombres de mots satisfont une relation de récurrence linéaire, il suffit de vérifier qu'elles sont égales sur leur premiers termes, en fait pour jusqu'au produit du nombre d'états de et de . Le nombre de mots de longueur acceptés par un automate peut être calculé sur l'image commutative[4].
Universalité et équivalence
Le problème de l'universalité, c'est-à-dire de savoir si un automate accepte tous les mots, et le problème de l'équivalence, c'est-à-dire de savoir si deux automates acceptent les mêmes mots, sont tous deux dans la classe PTIME, par réduction au problème de l'inclusion.
Extensions
Le coût en place de la transformation d'un automate inambigu en un automate déterministe est difficile à borner. Pour des alphabets unaires, une minoration est donnée par Okhotin[7] à l'aide d'une fonction arithmétique liée à la fonction de Landau.
La notion d’ambiguïté s'étend aux transducteurs finis : un transducteur est fonctionnel si la transformation qu'il réalise est une fonction (partielle), il est inambigu si, pour tout mot, il existe un seul calcul de la valeur de la fonction. Il est décidable si la transduction réalisée par un transducteur est une fonction.
Il y a aussi une interprétation algébrique naturelle du degré d’ambiguïté au moyen d'automates pondérés : on associe à chaque transition le poids 1 dans le monoïde des entiers naturels ; le poids associé à un mot est alors la simplement le nombre de chemins acceptant ce mot.
Enfin, il existe la même notion pour les mots infinis et les automates les reconnaissants comme les automates de Büchi. Dans ce cas, il y a différence entre automates non déterministes et automates déterministes, puisque ces derniers reconnaissent moins de langages. Les automates de Büchi inambigus reconnaissent les mêmes langages que les automates de Büchi non déterministes[4] - [8].
L'ambiguïté d'un automate fini est simplement relié à la notion d'ambiguïté dans les grammaires formelles par la biais de la correspondance entre les automates et les grammaires régulières : chaque dérivation dans une grammaire régulière correspond à un calcul dans l'automate correspondant. C'est d'ailleurs la notion de grammaire qui est mise en avant dans l'article historique de Stearns et Hunt[5]
Complexité des opérations
La complexité inambigüe d’un langage, notée usc(L) (pour « unambiguous state complexité ») est par définition le nombre minimal d’états d’un automate inambigu reconnaissant le langage L.
Bornes connues
Soient L, M des langages rationnels sur un alphabet commun, avec usc(L)=m et usc(M)=n. On a les résultats suivants[9] :
- image miroir : , où est le langage miroir ;
- intersection : , et la borne est atteinte sur un alphabet à au moins 2 lettres.
- quotient gauche : , et la borne est atteinte sur un alphabet à au moins 2 lettres.
- quotient droit : , et la borne est atteinte sur un alphabet à au moins 2 lettres.
- mélange :, et la borne est atteinte sur un alphabet à au moins 5 lettres.
- produit : , pourvu que , et la borne est atteinte sur un alphabet à au moins 6 lettres.
- étoile propre (opération plus) : , pourvu que , et la borne est atteinte sur un alphabet à au moins 3 lettres.
- étoile : , pourvu que , et la borne est atteinte sur un alphabet à au moins 3 lettres.
Il est intéressant de comparer la complexité des opérations sur les langages au moyen d' automates déterministes, d'automates inambigus et automates non déterministes. Pour cela, on introduit les notations :
- sc(L), nombre minimal d’états d’un automate déterministe reconnaissant le langage L.
- usc(L), comme ci-dessus le nombre minimal d’états d’un automate inambigu reconnaissant le langage L.
- nsc(L), nombre minimal d’états d’un automate non déterministe déterministe reconnaissant le langage L.
Dans la table suivante, les complexités sont résumées pour des langages donnés de complexité inambiguë n et m[9] :
| Opération | sc | nsc | usc |
|---|---|---|---|
| miroir | |||
| intersection | |||
| quotient gauche | |||
| quotient droit | |||
| étoile positive | |||
| étoile | |||
| mélange | |||
| produit | |||
| complément | [1] |
Calcul de minorants
Il existe une méthode générale pour calculer des minorants de la complexité inambigüe. Couplée avec la construction en général plus facile, d'un automate inambigu, elle fournit une borne inférieur à la complexité d'une opération sur les automates inambigus. La méthode est basée sur le calcul du rang d'une matrice associée à un automate ; elle a été développée par Schmidt dans une thèse non publiée de 1978, puis par Leung[10], et par Hromkovič et al.[11], et est reprise dans Jirásek et al.[9].
On considère un automate fini non déterministe sur un alphabet A, où et sont des ensembles d'états initiaux et terminaux.
Un état est dit accessible à partir de l'état par le mot s'il existe un chemin d'étiquette de à . Un ensemble d'états est dit accessible s'il existe un mot tel que est l'ensemble des états accessibles à partir d'un état initial par un chemin d'étiquette . On dit qu'un ensemble d'états est coaccessible si est accessible dans l'automate transposé de [12].
Les ensembles non vides d'états qui sont accessibles ou coaccessibles sont notés
- et
On a alors la propriété suivante :
- L'automate est inambigu si et seulement si deux ensembles d'états de et de quelconques ont au plus un élément en commun :
On s'en sert pour établir le résultat suivant, qui relie la complexité du langage au rang d'une matrice :
Théorème — Soit la matrice dont les lignes sont indicées par les éléments de et le colonnes indicées par les éléments de , et dont le coefficient d'indice est égal à 0 ou 1 selon que l'intersection de et est vide ou non. Alors on a .
Exemple
Pour vérifier que la complexité de l'intersection atteint bien la valeur pour des automates à et états, on considère des langages et automates particuliers, et on montre que l'automate pour l'intersection, qui a états, ne peut être remplacé par un automate inambigu plus petit à l'aide du théorème.
On considère les langages sur l'alphabet définis par et , pour et fixés. Ce sont donc les langages de mots contenant exactement lettres respectivement exactement lettres . Des automates inambigus (déterministe et incomplets) acceptant ces langages sont et , avec , , et les flèches de composées de pour et pour tout j, et pour composées de pour tout i et et pour .
L’automate produit est l’automate , où l'ensemble de flèches est composé des flèches pour et .
Tout ensemble singleton est accessible dans l’automate produit (par ), et est coaccessible (par ), et seuls des ensembles singletons sont accessibles ou coaccessibles. La matrice de l’énoncé est donc la matrice identité d’ordre , ce qui donne la borne inférieure pour l'intersection[9].
Notes et références
- Mikhail Raskin, « A superpolynomial lower bound for the size of non-deterministic complement of an unambiguous automaton », Arxiv, (arXiv 1711.03993). Accepté pour ICALP 2018 à Prague.
- Colcombet 2015.
- Allauzen, Mohri et Rastogi 2011.
- Löding 2013, Transparents.
- Stearns, Hunt, 1981.
- Meyer et Stockmeyer, 1972.
- Okhotin 2012.
- Arnold 1983.
- Jirásek et. al. 2016.
- (en) Hing Leung, « Descriptional complexity of nfa of different ambiguity », International Journal of Foundations of Computer Science, vol. 16, no 05, , p. 975–984 (DOI 10.1142/S0129054105003418)
- (en) Juraj Hromkovič, Sebastian Seibert, Juhani Karhumäki, Hartmut Klauck et Georg Schnitger, « Communication Complexity Method for Measuring Nondeterminism in Finite Automata », Information and Computation, vol. 172, no 2, , p. 202–217 (DOI 10.1006/inco.2001.3069)
- L'automate transposé est l'automate obtenu en inversant le sens des transitions, et en échangeant les états initiaux avec les états terminaux.
Bibliographie
- [Löding] Christof Löding, « Unambiguous Finite Automata », Developments in Language Theory, , p. 29–30 (lire en ligne) — Les transparents de sa présentation.
- [Isaak et Löding] Dimitri Isaak et Christof Löding, « Efficient inclusion testing for simple classes of unambiguous \u03c9-automata », Information Processing Letters, vol. 112, nos 14-15, , p. 578-582 (DOI 10.1016/j.ipl.2012.04.010, lire en ligne).
- [Meyer et Stockmeyer] Albert R. Meyer et Larry J. Stockmeyer, « The equivalence problem for regular expressions with squaring requires exponential space », 13th Annual Symposium on Switching and Automata Theory (SWAT 1972), Institute of Electrical & Electronics Engineers (IEEE), , p. 125-129 (DOI 10.1109/swat.1972.29).
- [Arnold] André Arnold, « Rational ω-languages are non-ambiguous », Theoretical Computer Science, vol. 26, nos 1-2, , p. 221-223 (DOI 10.1016/0304-3975(83)90086-5).
- [Okhotin] Alexander Okhotin, « Unambiguous finite automata over a unary alphabet », Information and Computation, vol. 212, , p. 15-36 (DOI 10.1016/j.ic.2012.01.003, lire en ligne).
- [Stearns et Hunt] Richard E. Stearns et Harry B. Hunt, « On the equivalence and containment problems for unambiguous regular expressions, grammars, and automata », 22nd Annual Symposium on Foundations of Computer Science (sfcs 1981), Institute of Electrical & Electronics Engineers (IEEE), , p. 74–81 (DOI 10.1109/sfcs.1981.29).
- [Allauzen et al.] Cyril Allauzen, Mehryar Mohri et Ashish Rastogi, « General algorithms for testing the ambiguity of finite automata and the double-tape ambiguity of finite-state transducers », International Journal of Foundations of Computer Science, vol. 22, no 04, , p. 883–904 (DOI 10.1142/S0129054111008477, arXiv 0802.3254)
- [Colcombet] Thomas Colcombet, « Unambiguity in Automata Theory », dans Descriptional Complexity of Formal Systems, coll. « Lecture Notes in Computer Science » (no 9118), (DOI 10.1007/978-3-319-19225-3_1, lire en ligne), p. 3–18
- [Jirásek et al.] Jozef Jirásek, Galina Jirásková et Juraj Šebej, « Operations on unambiguous automata », dans Developments in Language Theory, coll. « Lecture Notes in Computer Science » (no 9840), (DOI 10.1007/978-3-662-53132-7_20, lire en ligne), p. 243–255.


























































































