Automate transposé

Un automate A.

Le transposé de l'automate A.

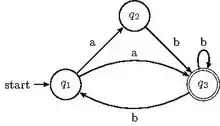
Soit un automate fini (déterministe ou non déterministe) ${\displaystyle {\mathcal {A}}=(Q,{\mathcal {F}},I,T)}$ où ${\displaystyle I}$ et ${\displaystyle T}$ sont les états initiaux et terminaux et où ${\displaystyle {\mathcal {F}}}$ est l'ensemble des transitions.

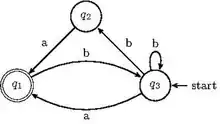
L'automate transposé[1] de ${\displaystyle {\mathcal {A}}}$ est l'automate obtenu en inversant le sens des transitions, et en échangeant les états initiaux avec les états terminaux. Formellement, c'est l'automate${\displaystyle {\mathcal {A}}^{R}}$.

${\displaystyle {\mathcal {A}}^{R}=(Q,{\mathcal {F}}^{R},T,I)}$,

où ${\displaystyle {\mathcal {F}}^{R}=\{(p,a,q)\mid (q,a,p)\in {\mathcal {F}}\}}$.

Le langage reconnu par l'automate transposé est formé des images miroir des mots reconnus par l’automate de départ.

En général, l'automate transposé n'est pas déterministe, mais la déterminisation de l'automate donne un automate déterministe minimal.

L'automate transposé est notamment utilisé dans l'algorithme de Brzozowski pour la minimisation d'un automate fini déterministe[2].

• graphe transposé, la notion analogue pour les graphes orientés.