Anomalie de survol planétaire
L’anomalie de survol est une incohérence entre les modèles scientifiques et les augmentations réelles de vitesse (une augmentation de l’énergie cinétique, par exemple) observée au cours d’un survol planétaire (le plus souvent, il s'agit de la Terre) par un vaisseau spatial. En de nombreuses occasions, on a observé que des vaisseaux prenaient plus de vitesse que les scientifiques ne l’avaient prédit, et jusqu’à ce jour, aucune explication satisfaisante n’a été trouvée. Cette anomalie a été relevée par des décalages Doppler dans la bande S et dans la bande X, ainsi que par télémétrie laser. Tout pris en compte, cela produit une augmentation de vitesse inexpliquée allant jusqu’à 13 mm/s au cours de ces survols[1].
Observations
Les explorations du système solaire ont systématiquement recours à l’assistance gravitationnelle. Le succès de ces manœuvres de survol dépend des paramètres précis de la trajectoire, c’est pourquoi la position et la vitesse du vaisseau sont relevées en permanence pendant le survol d’une planète par le Deep Space Network (DSN, réseau de communications avec l'espace lointain).
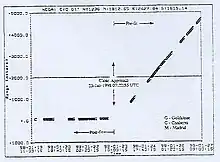
On a observé une première anomalie de survol grâce à une étude attentive des données DSN par Doppler peu après le survol de la Terre par la sonde Galileo le . Alors que ce qui est appelée différence Doppler (valeur observée moins valeur calculée par ordinateur), devait être nulle, l’analyse a révélé une différence inattendue de 66 mHz ce qui correspond à une augmentation de vitesse de 3,92 mm/s au périgée. Les recherches menées sur cette anomalie par le Jet Propulsion Laboratory (JPL), le Centre de vol spatial Goddard (GSFC) et par l’Université du Texas n’ont encore débouché sur aucune explication satisfaisante.
Aucune anomalie de ce type n'a été détectée après le deuxième survol de la Terre par la sonde Galileo, en , où la diminution de la vitesse mesurée correspondait à celle attendue du fait de la traînée atmosphérique à la plus basse altitude de 303 km. Cependant, les estimations de traînée avaient de grandes barres d'incertitude, et une accélération anormale ne pouvait donc pas être exclue[2].
Le , la vitesse de la sonde spatiale NEAR (Near Earth Asteroid Rendezvous) a augmenté anormalement de 13,46 mm/s après sa rencontre avec la Terre. La sonde Cassini–Huygens a gagné environ 0,11 mm/s en et Rosetta, 1,82 mm/s après son survol de la Terre en .
Une analyse de la sonde spatiale MESSENGER (qui étudie Mercure) n'a révélé aucune augmentation significative de la vitesse attendue. Cela peut être dû au fait que MESSENGER s’est approché et a quitté la Terre de manière symétrique par rapport à l’équateur (voir les données et l’équation proposée ci-dessous). Ceci suggère que l'anomalie pourrait être liée à la rotation de la Terre.
En , l'engin spatial Rosetta de l'ESA a été suivi de près pendant son survol terrestre en mesurant précisément sa vitesse, ceci afin de rassembler des données supplémentaires sur l'anomalie, mais aucune anomalie significative n'a été trouvée[3] - [4].
Le survol terrestre de Juno en 2013, en chemin pour Jupiter, n'a donné aucune accélération anormale[5].
En 2018, une analyse minutieuse de la trajectoire de l’astéroïde interstellaire 1I/ʻOumuamua a révélé un léger excès de vitesse lorsqu’il s’éloignait du Soleil. Les spéculations initiales ont suggéré que l'anomalie était due au dégazage, bien qu'aucun n'ait été détectée[6].
Un résumé pour quelques engins spatiaux ayant survolé la Terre est présenté dans le tableau ci-dessous[3] - [7].
| Quantity | Galileo-I | Galileo-II | NEAR | Cassini | Rosetta-I | MESSENGER | Rosetta-II | Rosetta-III | Juno | Hayabusa 2 | OSIRIS-REx[8] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | 1990-12-08 | 1992-12-08 | 1998-01-23 | 1999-08-18 | 2005-03-04 | 2005-08-02 | 2007-11-13 | 2009-11-13 | 2013-10-09 | 2015-12-03 | 2017-09-22 |
| Vitesse de libération, km/s | 8.949 | 8.877 | 6.851 | 16.01 | 3.863 | 4.056 | 4.7 | ||||
| Vitesse au périgée, km/s | 13.738 | — | 12.739 | 19.03 | 10.517 | 10.389 | 12.49 | 13.34 | 10.3 | 8.5 | |
| Paramètre d'impact, km | 11261 | 12850 | 8973 | 22680.49 | 22319 | ||||||
| altitude minimale, km | 956 | 303 | 532 | 1172 | 1954 | 2336 | 5322 | 2483 | 561[9] | 3090[10] | 17237 |
| Masse de la sonde, kg | 2497.1 | 730.40 | 4612.1 | 2895.2 | 1085.6 | 2895 | 2895 | ~2720 | 590 | ||
| Inclinaison orbitale sur l'équateur, degrés | 142.9 | 138.9 | 108.8 | 25.4 | 144.9 | 133.1 | |||||
| Angle de déflection, degrés | 47.46 | 51.1 | 66.92 | 19.66 | 99.396 | 94.7 | 80 | ||||
| Incrément de vitesse de libération, mm/s | 3.92±0.08 | −4.60±1.00 | 13.46±0.13 | −2±1 | 1.82±0.05 | 0.02±0.01 | ~0 | ~0 | 0±0.8[5] | ? | ? |
| Incrément de vitesse au périgée, mm/s | 2.56±0.05 | 7.21±0.07 | −1.7±0.9 | 0.67±0.02 | 0.008±0.004 | ~0 | −0.004±0.044 | ? | ? | ||
| Gain d'énergie, J/kg | 35.1±0.7 | 92.2±0.9 | 7.03±0.19 | ? | ? |
Recherches futures
BepiColombo et ses survols terrestres, prévus pour , font partie des missions à venir à ce sujet.
Certaines missions conçues pour étudier la gravité, telles que STEP, effectueront une mesure de la gravité extrêmement précise et pourraient éclaircir l'anomalie[11].
Équation proposée
Une équation empirique pour le changement anormal de vitesse de survol a été proposée par JD Anderson et al .:
où ωE est la fréquence angulaire de la Terre, RE est le rayon de la Terre et φi and φo sont les angles équatoriaux entrant et sortant de l'engin spatial[12]. Cette formule a été dérivée plus tard par Jean Paul Mbelek de la relativité restreinte, conduisant à l’une des explications possibles de l’effet[13]. Cela ne prend toutefois pas en compte les écarts relevés par l'USSSN - voir "Explications possibles" ci-dessous.
Explications possibles
Un certain nombre d'explications ont été proposées concernant l'anomalie de survol, notamment :
- L'effet Doppler transversal non pris en compte - c'est-à-dire le décalage vers le rouge de la lumière reçue due une vitesse radiale nulle et une vitesse tangentielle non nulle[13]. Cependant, cela ne peut pas expliquer l'anomalie dans toute la gamme des données disponibles.
- Un halo de matière noire autour de la Terre[14].
- Une modification de l'inertie résultant d'un effet Casimir, liée à l'effet Unruh et à la Quantized inertia[15].
- L'impact de la relativité générale, sous sa forme linéarisée et à champ faible, produisant des phénomènes gravitoélectriques et gravitomagnétiques dus à l'Effet Lense-Thirring, a également été étudié[16] : cela n'a pas expliqué les anomalies de survol.
- L'explication classique de la gravité retardée proposée par Joseph C. Hafele[17].
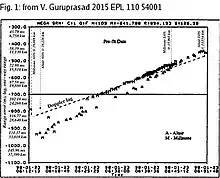
- L'excès de retard proportionnel à la portée du signal de télémesure révélé par les données de distance du réseau de surveillance spatiale des États-Unis lors du survol de NEAR[18]. Ce retard, qui tient compte de l'anomalie dans les données Doppler et de distance, ainsi que des oscillations Doppler restantes, à 10-20% près, indique des modes de modulation de fréquence en réception dus au taux Doppler, prédisant une anomalie positive uniquement lorsque le suivi par DSN est interrompu autour du périgée, et une anomalie nulle ou négative si le suivi est effectué en continu. Aucune anomalie ne devrait survenir en Doppler suivi par des stations non DSN[19].
- L'action d'un courant de torsion topologique prédisant des anomalies de survol dans la direction rétrograde, mais avec effet nul lorsque des engins spatiaux s'approchent de la planète dans une direction posigrade par rapport au sens de rotation de la planète[20].
- L'étude du survol de Juno a permis d'examiner les erreurs d'analyse qui pourraient potentiellement ressembler à une anomalie du survol. Ils ont constaté qu'un champ de gravité de haute précision (au moins 50×50 degrés/ordre [ préciser ]) était nécessaire pour des prévisions de survol précises. L'utilisation d'un champ de gravité de moindre précision générerait une erreur de vitesse de 4,5 mm/s[5].
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Flyby anomaly » (voir la liste des auteurs).
- « ESA's Rosetta spacecraft may help unravel cosmic mystery », European Space Agency, (consulté le )
- C, Edwards, J. Anderson, P, Beyer, S. Bhaskaran, J. Borders, S. DiNardo, W. Folkner, R. Haw, S. Nandi, F. Nicholson, C. 0ttenhoff, S. Stephens, « TRACKING GALILEO AT EARTH-2 PERIGEE USING THE TRACKING AND DATA RELAY SATELLITE SYSTEM », . Les deux méthodes de mesure ont donné des ajustements similaires aux données. Avec une incertitude de huit pour cent, les deux méthodes ont entraîné une diminution de la vitesse sur la trajectoire de −5,9 ± 0,2 mm / s. Les prévisions à priori pour le changement de vitesse induit par la traînée, basées sur le modèle de Jacchia-Roberts, étaient de −6,2 ± 4O mm / s [5], ce qui concorde clairement avec le changement de vitesse observé. En revanche, les données DSN du survol de la Terre de décembre 1990, à 956 km d'altitude, indiquaient une augmentation inexpliquée de la vitesse sur la trajectoire de 4 mm / s, après prise en compte des effets de traînée beaucoup moins importants. Compte tenu de l'incertitude des modèles de traînée, nous ne pouvons pas exclure de manière concluante la possibilité qu'une augmentation similaire se produise à la Terre 2. Par exemple, une augmentation non modélisée de 4 mm / s et une diminution de la traînée de -10 mm / s seraient compatibles avec nos résultats. et notre modèle atmosphérique a priori.
- « Mystery remains: Rosetta fails to observe swingby anomaly » [archive du ], ESA
- (en) J. Biele, « Navigation of the interplanetary Rosetta and Philae spacecraft and the determination of the gravitational field of comets and asteroids », (consulté le )
- Thompson, Paul F., Matthew Abrahamson, Shadan Ardalan et John Bordi « Reconstruction of Earth flyby by the Juno spacecraft. » () (lire en ligne)
—24th AAS/AIAA Space Flight Mechanics Meeting - Is the Interstellar Asteroid Really a Comet?
- (en) John D. Anderson, James K. Campbell et Michael Martin Nieto, The energy transfer process in planetary flybys, New Astronomy, (Bibcode 2007NewA...12..383A, arXiv astro-ph/0608087), p. 383–397
- Stephen Clark, « OSIRIS-REx asteroid mission receives gravitational boost from planet Earth », Spaceflight Now,
- NASA’S JUNO SPACECRAFT RETURNS 1ST FLYBY IMAGES OF EARTH WHILE SAILING ON TO JUPITER
- Hayabusa2 Earth Swing-by Result
- Jorge Páramos et G. Hechenblaikner, « Probing the Flyby Anomaly with the future STE-QUEST mission », Planetary and Space Science, vol. 79-80, , p. 76–81 (DOI 10.1016/j.pss.2013.02.005, Bibcode 2013P&SS...79...76P, arXiv 1210.7333)
- Anderson, « Anomalous Orbital-Energy Changes Observed during Spacecraft Flybys of Earth », Phys. Rev. Lett., (DOI 10.1103/physrevlett.100.091102, lire en ligne)
- (en) Auteur inconnu, « Special relativity may account for the spacecraft flyby anomalies », .
- (en) S.L.Adler, « Can the flyby anomaly be attributed to Earth-bound dark matter? », Physical Review D, (lire en ligne)
- (en) M. E. McCulloch, « Modelling the flyby anomalies using a modification of inertia », MNRAS Letters, (lire en ligne)
- (en) L. Iorio, « The Effect of General Relativity on Hyperbolic Orbits and Its Application to the Flyby Anomaly », Scholarly Research Exchange, (lire en ligne)
- http://www.ptep-online.com/2013/PP-33-01.PDF - Causal Version of Newtonian Theory by Time–Retardation of the Gravitational Field Explains the Flyby Anomalies
- Peter G. Antreasian et Joseph R. Guinn « Investigations into the Unexpected Delta-V Increase During the Earth Gravity Assist of GALILEO and NEAR » () (lire en ligne, consulté le )
—AIAA/AAS Astrodynamics Specialist Conf. and Exhibition - (en) V. Guruprasad, « Observational evidence for travelling wave modes bearing distance proportional shifts », EPL, (lire en ligne)
- (en) Mario J. Pinheiro, « Some effects of topological torsion currents on spacecraft dynamics and the flyby anomaly », MNRAS, (lire en ligne)
Voir aussi
Articles connexes
- Liste de problèmes non résolus de la physique
- Théorie MOND (théorie de la dynamique newtonienne modifiée)
- Anomalie Pioneer
- Effet Unruh
- Survol
Bibliographie
- (en) J. D. Anderson et J. G. Williams, « Long-range tests of the equivalence principle », Class. Quantum Grav., vol. 18, no 13, , p. 2447–2456 (DOI 10.1088/0264-9381/18/13/307, Bibcode 2001CQGra..18.2447A).
- (en) C. Lämmerzahl, O. Preuss et H. Dittus, « Is the physics within the Solar system really understood? », Proceedings of the 359th WE-Heraeus Seminar on "Lasers, Clocks, and Drag-Free: Technologies for Future Exploration in Space and Tests of Gravity", (Bibcode 2006gr.qc.....4052L, arXiv gr-qc/0604052).
- J. D. Anderson, J. K. Campbell et M. M. Nieto, « The Energy Transfer Process in Planetary Flybys », New Astronomy, vol. 12, no 5, , p. 383–397 (DOI 10.1016/j.newast.2006.11.004, Bibcode 2007NewA...12..383A, arXiv astro-ph/0608087).
- NASA Baffled by Unexplained Force Acting on Space Probes (2008), at Space.com.
- J. D. Anderson, J. K. Campbell, J. E. Ekelund, J. Ellis et J. F. Jordan, « Anomalous Orbital-Energy Changes Observed during Spacecraft Flybys of Earth », Phys. Rev. Lett., vol. 100, no 91102, , p. 091102 (PMID 18352689, DOI 10.1103/PhysRevLett.100.091102, Bibcode 2008PhRvL.100i1102A, lire en ligne [archive du ]).
- Wanted: Einstein Jr (2008), at Economist.com.
- K. Svozil, « Microphysical analogues of flyby anomalies », New Astronomy, vol. 12, no 5, , p. 383–397 (DOI 10.1016/j.newast.2006.11.004, Bibcode 2007NewA...12..383A, arXiv 0804.2198)
Liens externes
- Claus Lämmerzahl, « The Pioneer Anomaly or Do We Really Understand the Physics With the Solar System? » [pdf; 6.25 MB, talk/slides], sur Center for Applied Space Technology and Microgravity, University of Bremen, , p. 123
- Andreas Aste, « Spacecraft Anomalies: An Update » [pdf; 9.8 MB, talk/slides], sur Department of Physics, University of Basel, , p. 29
