Angles correspondants
En géométrie, deux droites coupées par une sécante déterminent quatre paires d'angles correspondants, dont les sommets sont aux points d'intersection.
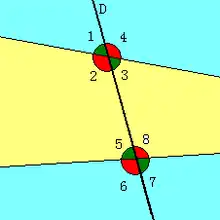
Droites coupées par une sécante D. Les 4 paires d'angles correpondants sont les paires {1;5}, {2,6}, {3,7} et {4,8}.
Les angles correspondants sont isométriques lorsque les deux droites sont parallèles.
Définition
On considère deux droites coupées par une sécante. Deux angles dessinés par cette figure sont dits correspondants lorsque[1] - [2]:
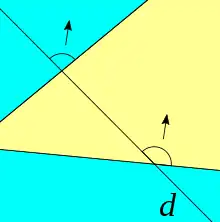
Angles correspondants « regardant dans la même direction ».
- ils sont du même côté de la sécante;
- ils ont des sommets différents;
- L'un est à l'intérieur de la zone découpée par les deux droites[3] tandis que l'autre est à l'extérieur de cette zone.
Il existe un moyen intuitif de déterminer les paires d'angles correspondants, c'est de repérer les angles qui «regardent dans la même direction»[4].
Propriétés
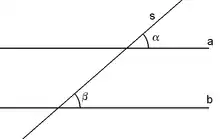
Les droites a et b sont parallèles et s est une sécante quelconque. Les angles α et β sont correspondants et de même mesure.
- Si deux droites parallèles sont coupées par une sécante, alors les angles correspondants ainsi formés sont égaux;
- Réciproquement, si deux droites coupées par une sécante forment des angles correspondants de même mesure, alors les deux droites sont parallèles;
- Si {α;β} est une paire d'angles correspondant et si α' et β' sont les angles opposés par le sommet des angles α et β, alors {α';β'} est aussi une paire d'angles correspondants.
Notes et références
- « Reconnaître des angles correspondants », sur Math-coatching.com
- Annette Braconne-Michoux, Enseigner la géométrie en contexte d’adaptation scolaire, JFD, (lire en ligne), p. 26
- Dans cette configuration, l'intérieur de la zone découpée par les deux droites est l'intersection des demi-plans dont les frontières sont les deux droites et contenant les deux sommets
- Yvan Monka, « angle et parallélisme », sur www.maths-et-tiques.fr, p. 3
Liens externes
- [vidéo] m@ths et tiques, Yvan Monka, Reconnaître des angles correspondants - Cinquième sur YouTube
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.