Alvéole d'abeille

La partie visible de chacune des alvéoles est un hexagone régulier dont le côté mesure environ 3 mm. La profondeur d‘une alvéole est de 11,5 mm. L'épaisseur de ses parois est d'environ un vingtième de millimètre. Chaque cellule est adossée à trois autres cellules au moyen d'une surface formée de trois losanges (rhombes).

Les alvéoles ne sont pas placées parfaitement à l'horizontale. Elles font un angle de 7 à 8 degrés vers le haut, pour éviter que le miel s'écoule hors des cellules (capillarité).

Les abeilles construisent spontanément des alvéoles d'environ 5 mm de diamètre (dimensions variables selon les variétés d'abeilles et la destination des alvéoles soit 4,8 mm pour les alvéoles de couvain et 5,3 mm pour les alvéoles de miel) mais celles des cires gaufrées disponibles dans le commerce mesurent de 5,4 à 5,7 mm[2].

Chaque cadre de corps de ruche Dadant a des dimensions intérieures de 41 × 26,5 cm. Il a donc une contenance théorique maximale de 82 × 53 = 4 346 alvéoles de 5 mm de largeur par face soit 8 692 par cadre mais les cadres étant rarement entièrement et parfaitement bâtis, on compte en moyenne 3 500 alvéoles par côté et donc 7 000 par cadres (et moitié moins pour un cadre de hausse).

Le volume intérieur des alvéoles se réduit au fur et à mesure que des naissances s'y produisent. Pour cette raison et pour des questions sanitaires, il convient de ne pas conserver plus de cinq ans un cadre bâti (avec le temps, il noircit, signe qu'il faut le remplacer).

La forme hexagonale des alvéoles fut repérée par Aristote dès le IV^e siècle av. J.-C.[3] - [4] (Histoire des animaux) puis traitée géométriquement huit siècles plus tard par Pappus, mathématicien grec[3] ; mais ce n’est qu’au XVIII^e siècle que cette forme rhomboïdale fut remarquée. Ainsi, Maraldi, astronome à l’Observatoire de Paris, détermina expérimentalement en 1712 la valeur des angles de ces rhombes, égale à 109° 28′ et 70° 32′[3] - [5].

Intrigué par la complexité de ces formes, l'astronome Johannes Kepler (faisant l'analogie entre la régularité de la disposition des alvéoles et celle des cristaux, il émet l'hypothèse que les abeilles ont un esprit mathématique dans sa conjecture énoncée en 1611[6]) et le physicien Réaumur[7], dans ses Mémoires pour servir à l'histoire des insectes, soupçonnent les abeilles de construire leur gâteau de cire dans un souci d’économie[8]. Afin de vérifier son hypothèse, il demanda au géomètre allemand König de déterminer quelle était la cellule hexagonale à fond composé de trois rhombes égaux qui pouvait être construite avec le moins de matière possible. Par calcul différentiel, König trouva en 1739 que les angles de ces losanges devaient être égaux à 109°26′ et 70°34′[8] - [3]. La correspondance de ce résultat avec celui de Maraldi est déjà étonnante, mais elle fut améliorée en 1743 par le mathématicien écossais Maclaurin[9] qui démontra que König avait commis une erreur dans ses calculs[3], et que les angles des losanges correspondant à l’utilisation d’un minimum de matière étaient justement ceux indiqués par Maraldi : 109° 28′ et 70° 32′[10] [les valeurs mathématiques optimales sont égales respectivement à Arc cos (-1/3) et Arc cos (1/3)]. c’est bien l’angle des faces de contact de 4 bulles de savon qui se rencontrent en un point. Les bulles de savon réalisent toujours, à cause de leur tension superficielle, la surface minimale à contrainte de contour donné.

C’est Réaumur qui propose l’idée originale et avant-gardiste de prendre comme unité de mesure le côté du pavage hexagonal et regrette beaucoup qu’il n’en fût pas fait de mesure dans les civilisations anciennes, car cela aurait donné une traçabilité des unités de mesure[11].

On retrouve sur ce problème : Lhuillier (Berlin, 1781)[12], Lalanne (Ann.sc.nat. 1840), Brougham (CRAS, 1858) et Hennessy (proc. roy. soc. London, 1886), avec évidemment Buffon et Guillaume-L. Formanoir de Palteau. Buffon émet une idée, souvent reprise hélas : qu’on comprime simultanément deux ensembles de cylindres de cire allongés ; ils prendront cette forme hexagonale[13]. C’est possible, mais les abeilles ne procèdent pas de cette manière[14] : elles commencent par construire le fond, puis les faces des cylindres hexagonaux. Elles ont donc en elles une adaptation à la construction d’un tel gaufrage du fond. Cela procède certes du tassement simultané en recto-verso de la cire, et l’explication de Buffon n’est donc pas à négliger, mais cela ne correspond pas à une situation de toutes les alvéoles, ensemble, comme on le voit écrit parfois.

Philip Ball rappelle qu'en 1660 le mathématicien danois Rasmus Bartholin avait suggéré que la forme hexagonale des alvéoles se formerait spontanément par la pression exercée par chaque abeille sur les parois (les abeilles ne faisaient donc pas preuve de talents de géomètre) alors que Charles Darwin avait proposé en 1859 que les abeilles construisaient initialement une alvéole circulaire qui devenait ensuite hexagonale[15].

Le premier souci des abeilles est de paver le plan pour pouvoir ensuite paver l’espace. On connaît trois polygones réguliers permettant de paver le plan : le triangle équilatéral, le carré et l’hexagone. Or, on peut démontrer que, parmi ces trois polygones réguliers, pour une même surface, l’hexagone est le polygone régulier offrant le plus petit périmètre.

Cependant, on pourrait se demander si l’hexagone est bien le pavage du plan le plus économique. En effet, on pourrait envisager de combiner des polygones de toutes sortes, qui ne sont pas forcément réguliers ni même dont les côtés forment une ligne droite. On ne savait pas grand-chose sur ce sujet jusqu’en 1943, date à laquelle le mathématicien hongrois László Fejes Tóth démontra que la structure hexagonale régulière restait le polygone le plus économique pour paver le plan parmi tous les polygones à côtés droits. Mais que se passe-t-il lorsque les côtés sont courbes ? Fejes Tóth pensait que la structure hexagonale régulière resterait pratiquement la plus efficace, mais montra qu'il existait une autre forme permettant une occupation encore plus optimale de l'espace et économisant aux abeilles 0,35 % de cire[16].

Ce n’est qu’en 1999 que Thomas Hales présente sa preuve en 19 pages (Théorème du nid d'abeille).

En 2013, le professeur Bhushan Lal Karihaloo (en) confirme la proposition de Darwin. Il montre que le travail incessant des ouvrières chauffe les gâteaux de cire alvéolaires circulaires à une température de 45 °C, la viscoélasticité permettant ainsi, par simple compression des alvéoles entre elles, de passer d'une forme circulaire à une forme hexagonale[17].

Le fond formé de trois losanges permet un adossement simple des alvéoles. Il est même facile de prouver qu’il est plus économique qu’un fond plat hexagonal mais reste-t-il le moyen le plus économique ?

En 1964, Fejes Toth a démontré que si le fond était formé de deux petits hexagones ainsi que de deux losanges, à la place de trois rhombes, la quantité de cire serait, pour un même volume, inférieure de 0,35 % à ce qu’elle est avec les losanges.

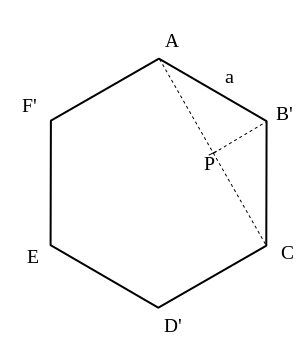
Pour déterminer les angles des rhombes minimisant la surface, on peut déjà remarquer que le remplacement d’un fond hexagonal AB′CD′EF′ par un fond formé de 3 rhombes de diagonales AC, CE, EF, ne modifie pas le volume de l’alvéole. En effet, le volume ôté est exactement égal au volume ajouté.

Il s’agit maintenant de comparer les surfaces.

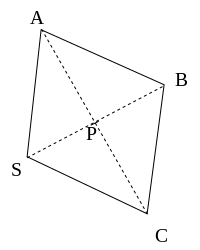Dans un fond rhomboïdal, la surface est celle de trois losanges SABC, SCDE, SEFA

Cette surface remplace exactement la surface du fond hexagonal AB′CD′EF′ et de 6 triangles égaux au triangle AB′B.

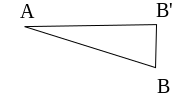
La position de B est optimale quand aire(SABC) - 2 × aire (AB′B) est minimale.

Or la diagonale du losange se calcule aisément ${\displaystyle AC=a{\sqrt {3}}}$. Si on appelle P le centre du losange, l’aire de SABC est alors ${\displaystyle a{\sqrt {3}}PB}$.

Quant au triangle AB′B, rectangle en B′, son aire vaut ${\displaystyle {\frac {1}{2}}a\times BB'}$

La quantité aire(SABC) - 2 × aire (AB′B) sera donc minimale si le chemin ${\displaystyle {\sqrt {3}}PB-BB'}$ est minimal

Deux méthodes sont alors possibles. L’une est accessible au niveau lycée, l’autre utilise le principe de Fermat.

Niveau lycée : on appelle x la longueur BB′, il s’agit alors de rendre minimale la quantité

${\displaystyle f(x)={\sqrt {3}}{\sqrt {{\frac {a^{2}}{4}}+x^{2}}}-x}$

Le calcul de la dérivée mène à

${\displaystyle f'(x)={\sqrt {\frac {3x^{2}}{{\frac {a^{2}}{4}}+x^{2}}}}-1}$

C’est une fonction croissante sur ${\displaystyle \mathbb {R} +}$ (car ${\displaystyle X\mapsto {\frac {3X}{X+a^{2}/4}}}$ est croissante) qui s’annule pour ${\displaystyle {\frac {x}{\sqrt {{\frac {a^{2}}{4}}+x^{2}}}}={\frac {1}{\sqrt {3}}}}$, c’est-à-dire lorsque ${\displaystyle {\frac {BB'}{BP}}={\frac {1}{\sqrt {3}}}}$.

C’est donc pour ce rapport que la fonction ${\displaystyle f\,}$atteint son minimum.

Principe de Fermat : il précise que le chemin ${\displaystyle {\sqrt {3}}PB-BB'}$ est minimal lorsque ${\displaystyle {\sqrt {3}}{\frac {\overrightarrow {PB}}{PB}}-{\frac {\overrightarrow {B'B}}{B'B}}}$ est orthogonal à ${\displaystyle {\overrightarrow {BB'}}}$ soit lorsque ${\displaystyle {\frac {BB'}{BP}}={\frac {1}{\sqrt {3}}}}$.

Il ne reste plus qu’à trouver les angles du losange. On appelle ${\displaystyle \theta ={\widehat {ABC}}}$ et ${\displaystyle \phi ={\widehat {SAB}}}$

• Dans le triangle PB′B, 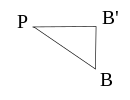on a

${\displaystyle {\frac {BB'}{BP}}={\frac {1}{\sqrt {3}}}=\cos({\widehat {B'BP}})}$

${\displaystyle {\frac {PB'}{BP}}={\frac {\sqrt {2}}{\sqrt {3}}}=\sin({\widehat {B'BP}})}$

ce qui donne

${\displaystyle BP={\frac {\sqrt {3}}{\sqrt {2}}}PB'}$

• Dans le triangle APB′

${\displaystyle AP={\sqrt {3}}PB'}$

• Donc, dans le losange SABC, on a
  • ${\displaystyle {\frac {PA}{PB}}={\sqrt {2}}=\tan(\theta /2)}$, ce qui donne ${\displaystyle \cos(\theta )={\frac {1-2}{1+2}}=-{\frac {1}{3}}}$
  • ${\displaystyle {\frac {PB}{PA}}={\frac {1}{\sqrt {2}}}=\tan(\phi /2)}$, ce qui donne${\displaystyle \cos(\phi )={\frac {1-1/2}{1+1/2}}={\frac {1}{3}}}$

soit des angles de 109°28′ et de 70°32′, comme l’a trouvé Mac Laurin.

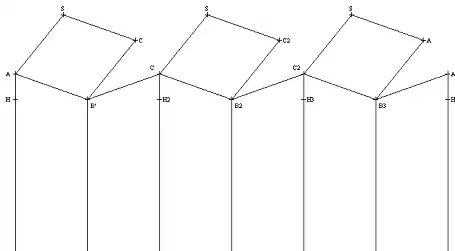
Développement d’une alvéole d’abeille