Conjecture de Kepler
La conjecture de Kepler est une ancienne conjecture (démontrée en 1998 et certifiée[1] en 2014) formulée par le physicien, astronome et mathématicien Johannes Kepler en 1611. Cette conjecture énonce que, pour un empilement de sphères égales, en espace libre, la densité maximale est atteinte pour un empilement compact de plans compacts. Cette densité d vaut environ 74 % :
- .
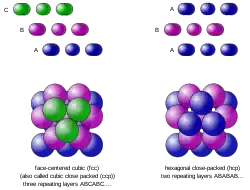

Dans un plan compact chaque sphère est au contact de six autres. Dans l'empilement compact de deux plans compacts chaque sphère du plan supérieur est posée dans le creux formé par trois sphères du plan inférieur en contact deux à deux. Si un plan compact est noté A, les autres plans compacts peuvent être de type A, B ou C selon leur décalage horizontal par rapport au plan A. L'empilement compact est réalisé par l'empilement de plans A, B ou C de telle sorte que deux plans successifs ne soient pas du même type : ABABAB… (empilement hc, pour hexagonal compact), ABCABCABC… (empilement cfc, pour cubique à faces centrées) mais aussi ABCBABCBABCB… et n'importe quel autre succession vérifiant la condition ci-dessus, même non périodique.
László Fejes Tóth démontre en 1953 que la conjecture de Kepler peut être réduite à un problème à un nombre fini de paramètres[2].
Preuve par ordinateur
En 1998, Thomas Hales annonce avoir démontré cette conjecture. Pour ce faire, il suit la voie ouverte par Tóth et réduit la démonstration à la recherche d'une borne inférieure à une fonction à 150 variables, pour un nombre élevé de configurations (plus de 5000), effectuée à l'aide de calculs par ordinateur impliquant la résolution d'environ 100 000 problèmes d'optimisation linéaire. Cette preuve reposait sur deux parties : l'une, classique, en forme de démonstration mathématique, l'autre basée sur des calculs fait à l'ordinateur. Mais la partie informatique n'était pas vérifiable, laissant un doute sur la validé du travail[3].
En 2003, au terme de 5 ans de vérifications, un groupe de 12 mathématiciens chargés de valider l'article de Hales affirment être « certains à 99 % » que cette démonstration est valide[4]. L'article de Hales est alors publié par la revue Annals of Mathematics. Cependant, le fait que de nombreux cas soient vérifiés à l'aide de calculs par ordinateur, et de façon liée, la compréhension réduite des principes généraux qui gouvernent la preuve, font que le doute subsiste qu'une erreur de détail qui n'a pas été repérée puisse affecter l'ensemble de la démonstration[4] (contrairement à une démonstration mathématique usuelle soigneusement relue, même si elle est très complexe comme celle du théorème de Fermat-Wiles[4]).
Pour cette raison, Hales lance le projet Flyspeck, visant à établir une preuve formelle de son théorème, qui puisse être validée à l'aide d'un assistant de preuve sur ordinateur, capable de vérifier que les étapes de la démonstration sont logiquement valides. Ce projet réunit des informaticiens et mathématiciens de plusieurs laboratoires.
En 2009, le prix Fulkerson est attribué à Hales (et conjointement à Samuel P. Ferguson, responsable des aspects calculatoires) pour cette démonstration, qui, bien que non encore validée par Flyspeck à ce moment, est considérée par la communauté mathématique comme complète.
Celle-ci est désormais validée[5] : Flyspeck est achevé en août et le rapport, inséré dans ArXiv[6], signé par 22 auteurs dont Hales, est proposé en janvier 2015. La preuve formelle est acceptée par le Forum of Mathematics en 2017[7].
Problème voisin
Le problème posé par Kepler se rapproche d'une autre question qui, selon la tradition, aurait surgi vers 1690 d'une polémique entre Newton et Gregory[8] : combien de sphères unités peut-on disposer autour d'une sphère centrale de même rayon ? Il est possible d'en disposer 12, mais la question est de savoir s'il est possible d'en disposer 13. Une réponse négative a été apportée en 1953 par Kurt Schütte et Bartel Leendert van der Waerden[9].
Notes et références
- Sean Bailly, « La conjecture de Kepler formellement démontrée », Pour la science, (consulté le ).
- (de) L. Fejes Tóth, Lagerungen in der Ebene, auf der Kugel und im Raum, Berlin, Springer, coll. « Grundlehren der mathematischen Wissenschaften » (no 65), (présentation en ligne), lien Math Reviews.
- Patrick Massot, « Pourquoi raconter des maths à un ordinateur », sur www.larecherche.fr (consulté le )
- (en) « The Flyspeck Project Fact Sheet ».
- (en) « Proof confirmed of 400-year-old fruit-stacking problem », sur New Scientist, .
- Thomas Hales, Mark Adams, Gertrud Bauer, Dat Tat Dang, John Harrison, Truong Le Hoang, Cezary Kaliszyk, Victor Magron, Sean McLaughlin, Thang Tat Nguyen, Truong Quang Nguyen, Tobias Nipkow, Steven Obua, Joseph Pleso, Jason Rute, Alexey Solovyev, An Hoai Thi Ta, Trung Nam Tran, Diep Thi Trieu, Josef Urban, Ky Khac Vu, Roland Zumkeller, « A formal proof of the Kepler conjecture », arXiv.org, (lire en ligne)
- https://doi.org/10.1017%2Ffmp.2017.1
- (en) Bill Casselman, « The Difficulties of Kissing in Three Dimensions », Notices of the AMS, vol. 51, no 8, , p. 884-885 (lire en ligne)
- Brian Hayes, « Les grappes de sphères collantes », Pour la Science, no 427, mai 2013, p. 64-71.
, dont les références étaient :
- (en) Tomaso Aste et Denis Weaire (en), The Pursuit of Perfect Packing, Institute of Physics Publishing, 2000 (ISBN 978-0-7503-0647-8)
- (en) Thomas C. Hales, « A Proof of the Kepler Conjecture », Ann. of Math., vol. 162, 2005, p. 1065-1185 [lire en ligne]
- (en) Thomas C. Hales, « Cannonballs and honeycombs », Notices Amer. Math. Soc., vol. 47, no 4, p. 440-449, [lire en ligne]« An elementary exposition of the proof of the Kepler conjecture. »
- (en) George G. Szpiro (de), Kepler's Conjecture, John Wiley & Sons, 2003 (ISBN 978-0-471-08601-7)
- (en) Thomas C. Hales, Mark Adams, Gertrud Bauer, Dat Tat Dang, John Harrison, Truong Le Hoang, Cezary Kaliszyk, Victor Magron, Sean McLaughlin, Thang Tat Nguyen, Truong Quang Nguyen, Tobias Nipkow, Steven Obua, Joseph Pleso, Jason Rute, Alexey Solovyev, An Hoai Thi Ta, Trung Nam Tran, Diep Thi Trieu, Josef Urban, Ky Khac Vu, Roland Zumkeller: A formal proof of the Kepler conjecture. CoRR abs/1501.02155 (2015)
Annexes
Articles connexes
- Conjecture d'empilement d'Ulam (en)
- Conjecture de Hadwiger (géométrie combinatoire)
- Empilement compact
Liens externes
- (en) Page personnelle de Thomas Hales
- (en) Revue de la démonstration de Hales
- (en) Article dans American Scientist - Dana Mackenzie
- (en) Site web du projet Flyspeck, dont le but (atteint) était d'établir une preuve formelle de la conjecture de Kepler.
- (en) Exemple concret de la conjecture de Kepler
