Algorithme de Karger
En algorithmique des graphes, l'algorithme de Karger est un algorithme probabiliste pour le problème de la coupe minimum (MIN-CUT). C'est donc un algorithme utilisant une source d'aléas, pour produire une solution correcte avec une bonne probabilité. Le problème en question est le suivant : étant donné un graphe non orienté trouver un ensemble de sommets non trivial minimisant le nombre d'arêtes sortant de cet ensemble.
L'outil principal de l'algorithme est la contraction aléatoire d'arêtes, qui fait décroître le nombre de sommets.
Il est dû à David Karger et a été publié en 1993[1]. Plusieurs variations ont ensuite été proposées.
Notion de coupe minimum
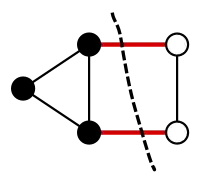
L'objet du problème est un graphe non orienté, un objet mathématique qui permet par exemple de représenter des réseaux de communications. Les nœuds du réseau sont appelés les sommets et les connexions sont les arêtes. Mathématiquement, un graphe non orienté G est la donnée d'un ensemble fini, noté V (les sommets) et d'un sous-ensemble E de V×V (les arêtes).
On parle de coupe pour désigner deux concepts proches : une partition des sommets en deux sous-ensembles non vides ou bien les arêtes ayant une extrémité dans chacun de ces sous-ensembles. Lorsqu'on parle du cardinal d'une coupe on entend le nombre d'arêtes de cette coupe. Une coupe minimum dans un graphe non orienté est une coupe de cardinal minimum. Il peut exister plusieurs coupes minimums.
Le concept de coupe minimum est relié à un autre concept fondamental en théorie des graphes, la notion de flot maximum. En effet le théorème flot-max/coupe-min établit qu'étant donné deux sommets particuliers s et t dans le graphe, le flot maximum pouvant passer par le réseau de s à t est égal au cardinal de la coupe minimum avec la contrainte que s doit être dans un sous-ensemble et t dans l'autre.
Problème de la coupe minimum
Le problème de la coupe minimum consiste, étant donné un graphe, à déterminer une coupe minimum. Ce problème peut être résolu de façon déterministe en cherchant un flot maximum entre toute paire de sommets grâce au théorème flot-max/coupe-min. Il existe de nombreux algorithmes pour cela, par exemple l'algorithme de Ford-Fulkerson ou l'algorithme de poussage/réétiquetage. L'algorithme de Karger est beaucoup plus simple[2] mais probabiliste.
Description de l'algorithme
Notion de contraction

L'algorithme est basé sur une procédure de contraction d'arête. Cette procédure consiste, étant donné un graphe G et une arête e=(a,b), à fusionner a et b pour former un unique sommet ab relié à la fois aux voisins de a et au voisins de b (hormis a et b). Le graphe ainsi formé est noté G/e. Cette transformation peut faire apparaître des arêtes en double si a et b partagent un voisin. Après plusieurs contractions on a des multi-arêtes et on travaille donc avec des multigraphes. Le point important est qu'une coupe dans le graphe après contraction, était déjà une coupe dans le graphe de départ[3].
Description informelle
L'algorithme consiste simplement à contracter une arête tirée uniformément dans le graphe, à la contracter, et à recommencer l'opération jusqu'à n'avoir que deux sommets. Les deux sommets représentent la partition de sommets, et les arêtes entre eux deux sont les arêtes de la coupe.
Un exemple d’exécution de l'algorithme est donné par l'image suivante.


Pseudo-code
Le pseudo-code est le suivant :
fonction contraction(G=(V,E)):
tant que |V| > 2
choisir e dans E aléatoirement (*fonction aléatoire uniforme*)
G ← G/e
retourner l'unique coupure de G
Analyse de l'algorithme
Terminaison
Le nombre de sommets du graphe est réduit de un à chaque étape, il y a donc n-2 étapes, et l'algorithme termine.
Probabilité d'erreur
Soit k la taille de la coupe minimum du graphe G, et soit C une telle coupe (vue comme un ensemble d'arêtes). Remarquons que le degré minimum de G est k sinon on pourrait isoler un sommet de bas degré et obtenir une coupe de taille inférieure à k. On cherche à savoir la probabilité d'avoir C à la fin de l'algorithme, c'est-à-dire la probabilité de n'avoir contracté aucune arête de C.
En notant n le nombre de sommet et l’événement « l'arête contractée à l'étape n'appartient pas à C » , on peut montrer[4] que
Donc la probabilité de succès est au moins .
En répétant l'algorithme fois, on peut avoir un algorithme avec une probabilité de succès constante. En effet la probabilité d'échec pour l'algorithme répété est au plus car les exécutions sont indépendantes. Cette quantité tend vers 1/e quand n tend vers l'infini.
Complexité
Pour un graphe donné sous forme de liste d'adjacence ou de matrice d'adjacence, un run de l'algorithme peut être implémenté en temps , on a donc une complexité quadratique en fonction du nombre de nœuds. Avec un nombre quadratique de répétitions on obtient un algorithme en .
Cette complexité peut être améliorée pour obtenir un algorithme quasi quadratique, de probabilité d'erreur tendant vers zéro avec n tendant vers l'infini[5].
Historique et extensions
L'algorithme de Karger a été inventé par Karger, et publié en 1993[1]. Plusieurs variations et développements ont ensuite été proposés. Par exemple la complexité a été améliorée par Karger et Stein[6]. Karger et Motwani ont montré que MIN-CUT était dans la classe de complexité appelée NC, en dérandomisant un autre algorithme utilisant le même principe de contraction[7] - [8].
L'algorithme de Karger est connu pour sa simplicité et est parfois utilisé pour introduire la notion d'algorithme probabiliste[9].
Notes et références
- David Karger, « Global Min-cuts in RNC and Other Ramifications of a Simple Mincut Algorithm », dans Proc. 4th Annual ACM-SIAM Symposium on Discrete Algorithms, (lire en ligne)
- Pour la simplicité, voir la phrase suivante dans Motwani et Raghavan 1995 : Note the extreme simplicity of the randomized algoritm we have just studied. In contrast, most deterministic algorithms for this problem are based on network flows and are considerably more complicated.
- Motwani et Raghavan 1995.
- Voir par exemple Motwani et Raghavan 1995.
- L'algorithme amélioré est décrit dans notes de cours sur l'algorithme de Karger, par Eric Vigoda (Georgia Institute of Technology), et l'article original est (Karger et Stein 1993).
- Version conférence : Karger et Stein 1993, version journal : Karger et Stein 1996
- David R. Karger et Rajeev Motwani, « Derandomization through approximation: An NC algorithm for minimum cuts », dans Proceedings of the twenty-sixth annual ACM symposium on Theory of computing, , p. 497-506
- Une dérandomisation consiste en la transformation d'un algorithme randomisé en un algorithme déterministe. Celle de l'article en question utilise des marches aléatoires sur des graphes expanseurs.
- Voir par exemple Motwani et Raghavan 1995 et les notes du cours de Sanjeev Arora (Université de Princeton (Today’s topic is simple but gorgeous: Karger’s min cut algorithm and its extension.).
Bibliographie
- (en) David Karger, « Global Min-cuts in RNC and Other Ramifications of a Simple Mincut Algorithm », dans Proc. 4th Annual ACM-SIAM Symposium on Discrete Algorithms, (lire en ligne)
- (en) David R. Karger et Clifford Stein, « An algorithm for minimum cuts », dans STOC, , p. 757-765
- (en) David R. Karger et Clifford Stein, « A new approach to the minimum cut problem », Journal of the ACM, vol. 43, no 4, , p. 601 (DOI 10.1145/234533.234534, lire en ligne)
- (en) Rajeev Motwani et Prabhakar Raghavan, Randomized Algorithms, Cambridge, New York et Melbourne, Cambridge University Press, (réimpr. 1997, 2000), 1re éd., 476 p. (ISBN 978-0-521-47465-8, lire en ligne), chap. 1 (« Introduction »), p. 7-9
Liens externes
- Nicolas Schabanel, « Description de l'algorithme en vidéo », sur Université Paris Diderot, .
- (en) Eric Vigoda, « Notes de cours sur l'algorithme de Karger », sur Georgia Institute of Technology,
- (en) Sanjeev Arora, « Notes de cours », sur Université de Princeton,
- (en) Sotiris Nikoletseas, « The Probabilistic Method - Randomized Algorithms (slides of lecture 1): A Monte Carlo Minimum Cut Algorithm », sur Université de Patras









