Algorithme de Kaprekar
En mathématiques, l’algorithme de Kaprekar est un algorithme qui transforme un nombre entier en un autre, de façon répétitive jusqu'à arriver à un cycle. Il fut découvert en 1949 par le mathématicien indien Dattatreya Ramachandra Kaprekar pour les nombres de quatre chiffres, mais il peut être généralisé à tous les nombres.
Description
L’algorithme de Kaprekar consiste à associer à un nombre quelconque n un autre nombre K(n) généré de la façon suivante :
- on considère un nombre n, écrit dans une base quelconque (généralement la base 10) ;
- on forme le nombre n1 en arrangeant les chiffres du nombre n dans l’ordre croissant et le nombre n2 en les arrangeant dans l’ordre décroissant ;
- on pose K(n) = n2 – n1 ;
- on itère ensuite le processus avec K(n).
Il existe aux moins trois variantes de cet algorithme suivant la façon dont on compte les chiffres avant de les arranger en ordre décroissant dans le nombre n2 :
- soit en prenant un nombre de chiffre fixes, y compris d'éventuels zéros initiaux supplémentaires : c'est la définition étendue ;
- soit en comptant malgré tout les chiffres nuls non-initiaux pour les grouper dans les unités : c'est une définition non stricte mais un peu moins étendue que la définition précédente (mais pour que l'algorithme fonctionne, la différence est calculée en valeur absolue au rang suivant de la suite, car l'algorithme normal suppose que n1 est supérieur à n2 : hors dans ce cas, ces chiffres nuls non-initiaux rangés en ordre croissant vont réduire le nombre de chiffres dans n1 mais pas dans n2, leur différence relative devenant alors négative si K(n) n'en retient pas la valeur absolue) ; une autre variante cependant peut cependant accepter de traiter les nombres initialement négatifs, en conservant le signe du nombre initial dans n1 et dans n2, et dans ce cas K(n) est défini pour tous les entiers relatifs, pas seulement les entiers naturels, et l'application répétée de K peut produire des suites de nombres dont le signe peut changer.
- soit en considérant un nombre réductible de chiffres, en ignorant tous les chiffres nuls avant de les ranger dans n1 et n2 : c'est la définition stricte (celle voulue par Kaprekar, où les chiffres nuls sont toujours rangés au début en poids fort, avant tous les autres).
La différence se voit dans la façon d'arranger les chiffres en ordre décroissant dans le nombre n2 puisque, dans la définition stricte (celle décrite par Kaprekar lui-même), le chiffre des unités de ce nombre ne peut alors pas être nul (et donc, par exemple, le nombre 09, qui comporte deux chiffres dans la définition étendue, n'en a qu'un dans la définition stricte). Dans les deux variantes, cela n'a pas d'effet sur le nombre n1. Selon les sources, l'une ou l'autre des définitions est utilisée mais l'algorithme (ou routine) obtenu n'est pas le même et ne donne pas le même résultat pour K(n) : davantage de nombres vont dégénérer avec moins de chiffres avec la définition stricte.
Pour les nombres à 4 chiffres, Kaprekar a décrit les nombreux cas pour lesquels la séquence dégénère (avec la définition stricte) en nombres ayant moins de chiffres : c'est le cas pour tout nombre comportant des zéros initiaux (et plus généralement tout nombre ayant au moins un chiffre nul, quel qu'en soit la position), ou tout nombre dont les chiffres sont déjà rangés en ordre décroissant (y compris les nombres dont tous les chiffres sont identiques).
Exemples
- En partant du nombre 52 (en base 10), on obtient successivement (en définition étendue): 52, 27, 45, 09, 81, 63, 27, etc. Et la séquence se répète alors en un cycle de 5 nombres. En définition stricte, la séquence dégénère en 52, 27, 45, 9, et enfin 0 qui ne varie plus (tous les nombres à deux chiffres en définition stricte dégénèrent en 0).
- En partant du nombre 634 (en base 10), on obtient successivement : 297, 693, 594, 495, 495, etc. On obtient là un nombre qui ne varie plus (mais qui ne dégénère dans aucune des deux définitions).
- En partant du nombre 5 294 (en base 10), on obtient K(5 294) = 9 542 - 2 459 = 7 083. En répétant le processus, K(7 083) = 8 730 - 378 = 8 352. Puis, K(8 352) = 6 174. On constate que K(6 174) = 6 174 et que l’algorithme conduit alors à un nombre fixe.
- En partant du nombre 63 954 (en base 10), on obtient 61 974, 82 962, 75 933, 63 954, 61 974, etc. La séquence se répète en un cycle de 4 nombres.
Cycles
Pour tout nombre initial et selon la base de numération utilisée, l’algorithme de Kaprekar produit finalement l’une des possibilités suivantes :
- le nombre constant zéro, y compris dans les « cas dégénérés » où tous les chiffres du nombre initial sont égaux (c'est-à-dire le cas du nombre initial 0 et les 9 cas de nombres décimaux initiaux ayant un nombre donné de chiffres tous identiques et non nuls), ainsi que (plus généralement) ceux dont les chiffres sont déjà ordonnés du plus grand au plus petit (mais peuvent être répétés) ; cependant, Kaprekar lui-même excluait du comptage des cas les nombres ayant des chiffres initiaux nuls (qui ne sont alors pas réordonnés comme chiffres finaux dans le nombre n2 de l'algorithme de définition), ce qui réduit les cas dégénérés aux seuls cas du nombre zéro lui-même et des nombres formés de chiffres identiques non nuls ;
- un nombre constant ayant le même nombre de chiffres que le nombre initial (seulement valide pour cette base), appelé parfois « constante (cyclique) de Kaprekar » (terminologie désuète, à ne pas confondre avec un nombre de Kaprekar) ;
- un cycle fini de nombres ayant le même nombre de chiffres (la longueur du cycle est nécessairement ornée par la base de numération et par le nombre de chiffres du nombre dans cette base, mais est très inférieur à la quantité de nombres dans ces limites ; mais il y a plusieurs cycles possibles selon le nombre initial, y compris l'ordre initial de ses chiffres).
Pour la base 10, les premières possibilités sont les suivantes :
| Nb. de chiffres | Nb. de cas | Période | Description | Valeur constante ou suite cyclique de nombres |
|---|---|---|---|---|
| 0 | 1 cas | 1 | Cas dégénérés | 0 |
| 1 | 9 cas | 1 | Cas dégénérés | 0 |
| 2 | 9 cas | 1 | Cas dégénérés | 0 |
| 81 cas | 1 | Cas dégénérés (définition stricte) | 0 | |
| 5 | Cycle (définition étendue) | 81 ; 63 ; 27 ; 45 ; 09 | ||
| 3 | 9 cas | 1 | Cas dégénérés | 0 |
| 891 cas | 1 | Constante | 495 | |
| 4 | 9 cas | 1 | Cas dégénérés | 0 |
| 8 991 cas | 1 | Constante | 6 174 | |
| 5 | 9 cas | 1 | Cas dégénérés | 0 |
| 3 002 cas | 2 | Cycle | 59 994 ; 53 955 | |
| 43 219 cas | 4 | Cycle | 71 973 ; 83 952 ; 74 943 ; 62 964 | |
| 43 770 cas | 4 | Cycle | 82 962 ; 75 933 ; 63 954 ; 61 974 | |
| 6 | 9 cas | 1 | Cas dégénérés | 0 |
| 1 815 cas | 1 | Constante | 549 945 | |
| 56 180 cas | 1 | Constante | 631 764 | |
| 841 996 cas | 7 | Cycle | 851 742 ; 750 843 ; 840 852 ; 860 832 ; 862 632 ; 642 654 ; 420 876 | |
| 7 | 9 cas | 1 | Cas dégénérés | 0 |
| 8 999 991 cas | 8 | Cycle | 9 529 641 ; 8 719 722 ; 8 649 432 ; 7 519 743 ; 8 429 652 ; 7 619 733 ; 8 439 552 ; 7 509 843 | |
| 8 | 9 cas | 1 | Cas dégénérés | 0 |
| 556 234 cas | 1 | Constante | 63 317 664 | |
| 2 041 186 cas | 1 | Constante | 97 508 421 | |
| 43 200 472 cas | 3 | Cycle | 83 208 762 ; 86 526 432 ; 64 308 654 | |
| 44 202 099 cas | 7 | Cycle | 85 317 642 ; 75 308 643 ; 84 308 652 ; 86 308 632 ; 86 326 632 ; 64 326 654 ; 43 208 766 |
Notes :
- Le terme « Nb. de chiffres » se réfère au nombre de chiffres qui composent le nombre initialement choisi dans la base 10 de numération utilisée et qui peut produire le résultat considéré, sans compter les chiffres nuls initiaux pour des nombres ayant moins de chiffres et déjà couverts dans les rangées précédentes de la table.
- Les 81 cas des nombres à 2 chiffres produisant un cycle de 5 nombres n'est pas strict au sens voulu par Kaprekar, car le « cycle » engendre le nombre 09, qui devrait être vu non pas comme un nombre à deux chiffres mais comme le nombre 9, qui est dégénéré et génère ensuite la constante 0. Si autorise le comptage de zéros initiaux, d'autres « cycles étendus » peuvent apparaître mais seulement pour des nombres d'ordre de grandeur plus élevé que les premiers listés dans la table alors qu'ils dégénèrent à un ordre inférieur.
- Le nombre à 6 chiffres 851 742 (produisant un cycle de 7 nombres) est une anagramme de 142 857, lui-même un nombre de Kaprekar.
Constantes de Kaprekar
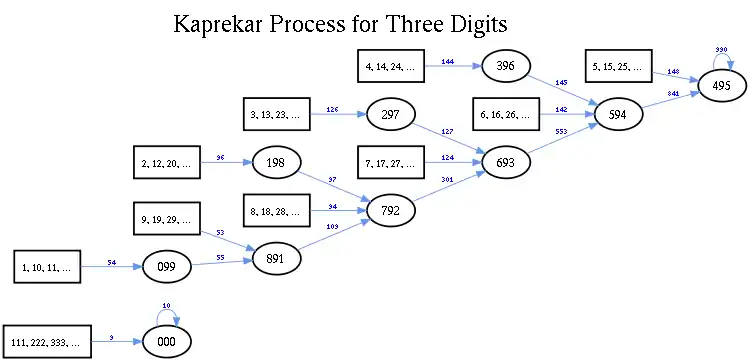
Constante pour les nombres à trois chiffres décimaux
La constante de Kaprekar pour les nombres entiers à trois chiffres tous différents est 495 :
- Il est facile de s'assurer qu'il s'agit bien d'un point fixe : 954 - 459 = 495.
- Le nombre le plus grand obtenu par l'algorithme est 910 - 019 = 891 = 9 * 99. Le nombre le plus petit obtenu par l'algorithme est 210 - 012 = 198 = 2 * 99.
- Les nombres obtenus via cet algorithme ont tous la même forme, soit un multiple de 99.
En effet, posons un nombre formé de 3 chiffres a, b, c tels que a > b > c.
- Le prochain nombre obtenu via l'algorithme est ainsi : 99 * (a - c).
- Observons que les multiples de 99 sont tels que, pour n = (a - c), on obtient : 99 * n = (n-1) * 100 + 9 * 10 + (10 - n).
- Les différents cas possibles sont facilement énumérés selon la relation d'ordre entre (n-1) et (10 - n). La possibilité que (n-1) = (10 - n) doit être immédiatement exclue, car n doit être un entier et 5.5 n'en est pas un.
Il reste les deux possibilités suivantes :
- (n - 1) < (10 - n), c'est-à-dire n < 5 (on sait que n > 1, car sinon on n'aurait que 2 chiffres)
- (n - 1) > (10 - n), c'est-à-dire n > 5 (on sait que n < 10, car le maximum de a - c est 9)
- Le cas où n = 5 donne 495, notre constante.
Selon la première éventualité, on obtient à l'itération suivante de l'algorithme : 99 * (10 - n). Énumérons tous les résultats possibles :
- n = 2 donne 99 * 8
- n = 3 donne 99 * 7
- n = 4 donne 99 * 6
Selon la seconde éventualité, on obtient à l'itération suivante de l'algorithme : 99 * (n - 1). Énumérons tous les résultats possibles :
- n = 6 donne 99 * 5
- n = 7 donne 99 * 6
- n = 8 donne 99 * 7
- n = 9 donne 99 * 8
On peut donc conclure que le nombre 495 est obtenu en au plus 5 itérations de l'algorithme.
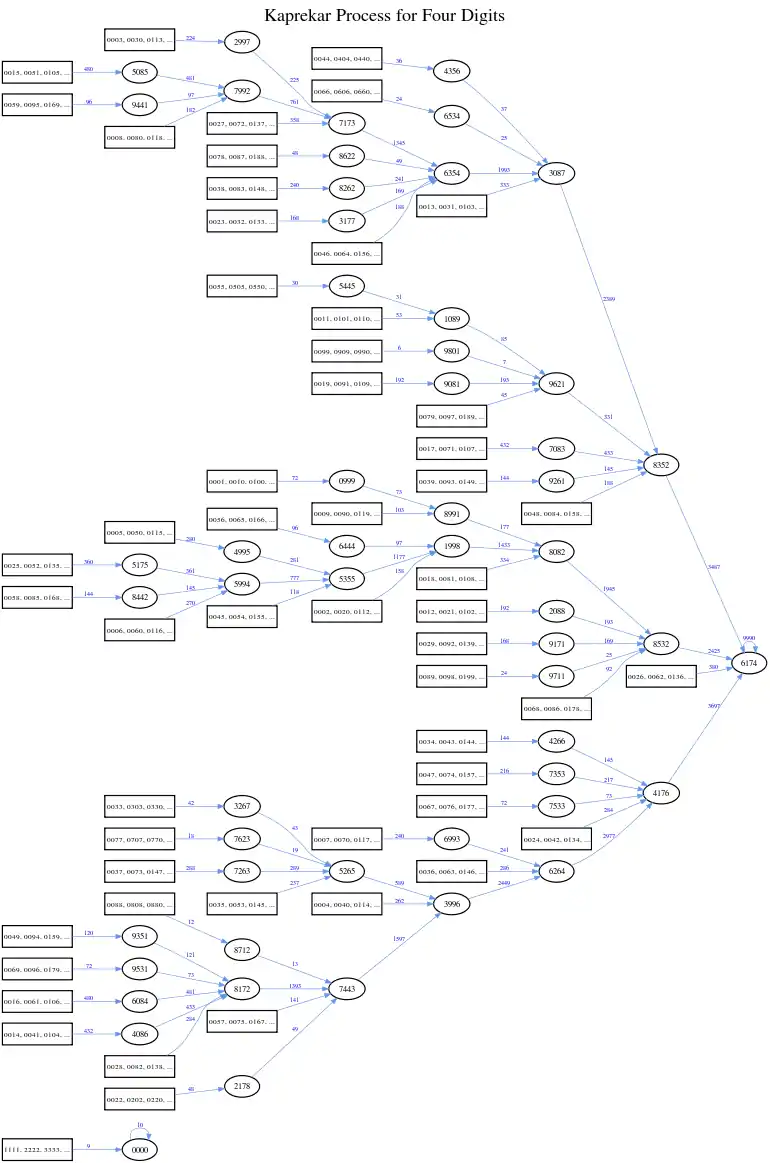
Constante pour les nombres à quatre chiffres décimaux
La constante de Kaprekar pour les nombres à quatre chiffres décimaux pas tous pareils est le nombre 6 174[1]. C'est le nombre auquel se stabilise toute suite générée par l'algorithme de Kaprekar à partir d'un nombre de quatre chiffres non tous égaux. Exemple :
- u0 = 2545
- u1 = 5542 – 2455 = 3087
- u2 = 8730 – 378 = 8352
- u3 = 8532 – 2358 = 6174
- u4 = 7641 – 1467 = 6174.
La relation entre toutes ces constantes est que la somme des chiffres qui composent chacun de ces nombres est obligatoirement un multiple de 9 et que les nombres eux-mêmes sont obligatoirement des multiples de 9 (pour la base 10), et de façon générale un multiple du plus grand chiffre de la base de numération utilisée. Selon le nombre de chiffres du nombre entier initial, il peut exister plusieurs constantes de Kaprekar.
Notes et références
- (en) Eric W. Weisstein, « Kaprekar's routine », sur MathWorld.