Algorithme de Gram-Schmidt

En algèbre linéaire, dans un espace préhilbertien (c'est-à-dire un espace vectoriel sur le corps des réels ou celui des complexes, muni d'un produit scalaire), le procédé ou algorithme de Gram-Schmidt[1] est un algorithme pour construire, à partir d'une famille libre finie, une base orthonormée du sous-espace qu'elle engendre. On peut aussi utiliser le procédé de Gram-Schmidt sur une famille infinie dénombrable de vecteurs. Ceci permet de démontrer l'existence d'une base hilbertienne si l'espace est séparable.

Énoncé

Précisément, en notant $N = {0,..., p}$ avec $p$ dans $ℕ$ , ou $N = ℕ$ :

Théorème — Si $(x_{n})_{n\in N}\,$ est une famille libre d'un espace préhilbertien, il existe une et une seule famille orthonormée $(e_{n})_{n\in N}\,$ telle que :

${\rm {Vect}}(e_{0},\ldots ,e_{n})={\rm {Vect}}(x_{0},\ldots ,x_{n})\,$ pour tout $n$
les produits scalaires $(e_{n}|x_{n})\,$ sont strictement positifs pour tout $n$

On oublie souvent la seconde condition, qui assure l'unicité. Elle permet de parler de la famille orthonormalisée de Gram-Schmidt associée à $(x_{n})_{n\in N}\,$ .

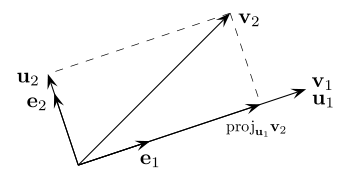
L'étape générale de l'algorithme consiste à soustraire au vecteur $v j +1$ son projeté orthogonal sur le sous-espace engendré par $v 0,..., v j$ . On s'appuie sur la famille orthonormale déjà construite pour le calcul de ce projeté.

Cette méthode a été publiée par Jørgen Pedersen Gram en 1883 et reformulée par Erhard Schmidt en 1907, mais on la trouve déjà dans des travaux de 1816 de Laplace[2].

Applications

Le procédé d'orthonormalisation de Gram-Schmidt donne constructivement l'existence de bases orthonormées pour tout espace euclidien ou hermitien.
On peut aussi orthonormaliser la base canonique (1,X, …) de ℝ[X] et obtenir ainsi une famille de polynômes orthogonaux.
Le procédé de Schmidt peut être utilisé dans la décomposition QR d'une matrice[3].

Procédé de Gram-Schmidt

Nous définissons l'opérateur de projection orthogonale sur une droite vectorielle dirigée par le vecteur $u$ par[4] :

\mathrm {proj} _{\mathbf {u} }\,(\mathbf {v} )={\langle \mathbf {u} ,\mathbf {v} \rangle  \over \langle \mathbf {u} ,\mathbf {u} \rangle }\mathbf {u} .

Le procédé de Gram-Schmidt est alors :

Les deux premières étapes du procédé de Gram–Schmidt.

	$\mathbf {u} _{1}=\mathbf {v} _{1},$		$\mathbf {e} _{1}={\mathbf {u} _{1} \over \\|\mathbf {u} _{1}\\|}$
	$\mathbf {u} _{2}=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{2}),$		$\mathbf {e} _{2}={\mathbf {u} _{2} \over \\|\mathbf {u} _{2}\\|}$
	$\mathbf {u} _{3}=\mathbf {v} _{3}-\mathrm {proj} _{\mathbf {u} _{1}}\,(\mathbf {v} _{3})-\mathrm {proj} _{\mathbf {u} _{2}}\,(\mathbf {v} _{3}),$		$\mathbf {e} _{3}={\mathbf {u} _{3} \over \\|\mathbf {u} _{3}\\|}$
	$\vdots$		$\vdots$
	$\mathbf {u} _{k}=\mathbf {v} _{k}-\sum _{j=1}^{k-1}\mathrm {proj} _{\mathbf {u} _{j}}\,(\mathbf {v} _{k}),$		$\mathbf {e} _{k}={\mathbf {u} _{k} \over \\|\mathbf {u} _{k}\\|}$

Avec :

$< , >$ , le produit scalaire dans l'espace considéré
$v 1, ..., v k$ , un ensemble de vecteurs non liés
$u 1, ..., u k$ , un ensemble de vecteurs orthogonaux deux à deux
$e 1, ..., e k$ , l'ensemble de vecteurs orthonormaux deux à deux recherché

Démonstration

La démonstration du résultat se fait par récurrence, en montrant à chaque étape que le vecteur $u k$ est orthogonal aux vecteurs construits aux étapes précédentes.

À l'étape 1, il n'y a qu'un seul vecteur, donc la propriété est vérifiée.
À l'étape 2, on a, par linéarité à droite du produit scalaire :

\langle \mathbf {u} _{1},\mathbf {u} _{2}\rangle =\left\langle \mathbf {v} _{1},\mathbf {v} _{2}-{\frac {\langle \mathbf {v} _{1},\mathbf {v} _{2}\rangle }{\langle \mathbf {v} _{1},\mathbf {v} _{1}\rangle }}\mathbf {v} _{1}\right\rangle =\left\langle \mathbf {v} _{1},\mathbf {v} _{2}\right\rangle -{\frac {\langle \mathbf {v} _{1},\mathbf {v} _{2}\rangle }{\langle \mathbf {v} _{1},\mathbf {v} _{1}\rangle }}\left\langle \mathbf {v} _{1},\mathbf {v} _{1}\right\rangle =0

donc $(u 1, u 2)$ sont bien orthogonaux

À l'étape k, supposons donc que $u 1, ..., u k -1$ sont bien orthogonaux deux à deux. Alors, toujours par linéarité à droite du produit scalaire :

\forall i\neq k,\langle \mathbf {u} _{i},\mathbf {u} _{k}\rangle =\left\langle \mathbf {u} _{i},\mathbf {v} _{k}-\sum _{j=1}^{k-1}{\frac {\langle \mathbf {u} _{j},\mathbf {v} _{k}\rangle }{\langle \mathbf {u} _{j},\mathbf {u} _{j}\rangle }}\mathbf {u} _{j}\right\rangle =\left\langle \mathbf {u} _{i},\mathbf {v} _{k}\right\rangle -\sum _{j=1}^{k-1}{\frac {\langle \mathbf {u} _{j},\mathbf {v} _{k}\rangle }{\langle \mathbf {u} _{j},\mathbf {u} _{j}\rangle }}\left\langle \mathbf {u} _{i},\mathbf {u} _{j}\right\rangle =\left\langle \mathbf {u} _{i},\mathbf {v} _{k}\right\rangle -{\frac {\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle }{\langle \mathbf {u} _{i},\mathbf {u} _{i}\rangle }}\left\langle \mathbf {u} _{i},\mathbf {u} _{i}\right\rangle =0

Ce qui permet de conclure.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Gram–Schmidt process » (voir la liste des auteurs).

Mathématiques Tout-en-un. 2^e année MP, Paris, Dunod, 2004, 2^e éd., 1279 p. (ISBN 978-2-10-007576-8, BNF 39237416), p. 569
(en) Gram-Schmidt orthogonalization, dans Earliest Known Uses of Some of the Words of Mathematics (G)
A. Quarteroni, R. Sacco, F. Saleri, Méthodes numériques pour le calcul scientifique, Programmes en Matlab, éd. Springer, 2000, p. 83 et suiv. Lire en ligne
La convention choisie pour le produit scalaire hermitien étant ici : linéarité à droite et semi-linéarité à gauche.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.