Algorithme de Bowyer-Watson

En géométrie algorithmique, l'algorithme de Bowyer-Watson est une méthode pour calculer la triangulation de Delaunay d'un ensemble fini de points dans un espace euclidien de dimension quelconque[1].

Il est parfois appelé « algorithme de Bowyer » ou « algorithme de Watson », Adrian Bowyer et David Watson l'ayant indépendamment découvert et publié dans le même numéro du Computer Journal en 1981[1] - [2].

Description

Première étape : insertion d'un point dans un « super-triangle » englobant.
Insertion d'un second point.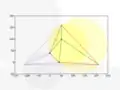
Insertion d'un troisième point.
Insertion d'un quatrième point.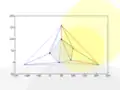
Insertion d'un cinquième (et dernier) point.
Suppression des arêtes du super-triangle.

L'algorithme de Bowyer-Watson est un algorithme itératif. Il procède en ajoutant des points, un à la fois, à une triangulation de Delaunay valide du sous-ensemble des points. Après chaque insertion, tous les triangles dont le cercle circonscrit (en jaunes dans les figures ci-dessus) contient le nouveau point sont supprimés, laissant un trou polygonal « étoilé » (en rouge) qui est alors re-triangulé (en vert) en utilisant le point suivant.

Super-Triangle

Les points à trianguler doivent être compris dans un triangle englobant.

Un tel triangle peut être le triangle dont le cercle inscrit est le cercle minimal englobant.

Plus simplement, dans un espace à 2 dimensions, pour un ensemble de points $P=\left\{p=(p_{x},p_{y})\right\}$ , le triangle $A=(x_{min}-\epsilon ,y_{min}-\epsilon )$ , $B=\left(x_{min}+2(x_{max}-x_{min})+3\epsilon ,y_{min}-\epsilon \right)$ , $C=\left(x_{min}-\epsilon ,y_{min}+2(y_{max}-y_{min})+3\epsilon \right)$ englobe tous ces points. En effet, par réduction d'échelle et translation tous les points peuvent être ramenés dans le carré $0\leq x\leq 1,0\leq y\leq 1$ , compris dans le triangle $\left\{(0,0),(2,0),(0,2)\right\}$ .

Trou polygonal

Les arêtes du trou polygonal résultant de la suppression des triangles sont les arêtes des mêmes triangles dont le triangle opposé (le triangle partageant la même arête) est soit absent (bord du super-triangle) soit parmi les triangles à conserver.

Un parcours des arêtes dans le sens trigonométrique permet de sélectionner les arêtes du trou polygonal dans le sens trigonométrique:

à partir d'un triangle à supprimer aléatoire et d'une de ses arêtes.
trouver le triangle opposé :
- si ce triangle existe et fait partie des triangles à supprimer: sélectionner ce triangle et la prochaine arête sur ce triangle dans le sens trigonométrique
- sinon ajouter l'arête et l'ajouter à la construction du polygone, puis sélectionner la prochaine arête du triangle dans le sens trigonométrique
continuer le parcours des arêtes tant que le polygone n'est pas fermé

triangles = [...]
englobant = []
triangle_supprimer = [...]
triangle = triangle_supprimer[0]
arete = (triangle[0], triangle[1])
while not polygone_ferme(englobant):
    t_voisin = triangles.triangle_oppose(arete)
    if t_voisin in triangle_supprimer:
        triangle = t_voisin
        arete = t_voisin.prochaine_arete(arete)
    else:
        englobant.append(arete)
        arete = triangle.prochaine_arete(arete)

Pseudo-code

Le pseudocode suivant à une compexité en temps de $O(n^{2})$ . Néanmoins il existe des optimisations pour obtenir une complexité de $O(n\log n)$ , par exemple en trouvant le triangle contenant le nouveau point dans son cercle circonscrit, sans avoir à vérifier tous les triangles.

def delaunay_bowyer_watson( points ):
    supertri = supertriangle(points) # Un triangle contenant tous les points à trianguler.
    # Qui devient le premier triangle de la triangulation.
    triangles = [ supertri ]
    fait = { supertri: False }
    for sommet in points:
        # Tous les triangles dont le cercle circonscrit contient le sommet à ajouter sont identifiés,
        # l'ensemble de leurs arêtes forment un polygone englobant.
        # Démarrer avec un polygone englobant vide.
        englobant = []
        # Pour l'instant, il n'y a aucun triangle subdivisé y supprimer.
        à_supprimer = []
        for triangle in triangles:
            centre,rayon = cercle_circonscrit( triangle )
            # Si ce triangle respecte la condition de Delaunay.
            if x(centre) < x(sommet) and abs(x(sommet)-x(centre)) > radius:
                fait[triangle] = True # Le marquer comme traité.
            # Si le sommet courant est dans le cercle circonscrit du triangle courant,
            if dans_cercle( sommet, centre, rayon ):
                # ajouter les arêtes de ce triangle au polygone candidat,
                englobant += aretes( triangle )
                # préparer la suppression de ce triangle.
                à_supprimer += [ triangle ]
                fait.pop( triangle )
        # Effectue la suppression des triangles marqués précédemment.
        for triangle in à_supprimer:
             triangles.remove( triangle )
        # Créer de nouveaux triangles, en utilisant le sommet courant et le polygone englobant.
        for arête in englobant:
            point_A, point_B = arête
            # Ajoute un nouveau triangle à la triangulation.
            triangle = [ point_A, point_B, sommet ]
            triangles += [ triangle ]
            # Il faudra le considérer au prochain ajout de point.
            fait[triangle] = False
    # Supprime les triangles ayant au moins une arête en commun avec le super-triangle.
    triangulation = non_supertriangle( triangles )
    return triangulation

Voir aussi

Cet algorithme peut être utilisé pour obtenir un diagramme de Voronoi des points, qui est le graphe dual de la triangulation de Delaunay.

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bowyer–Watson algorithm » (voir la liste des auteurs).

(en) David F. Watson, « Computing the n-dimensional Delaunay tessellation with application to Voronoi polytopes », Comput. J., vol. 24, n^o 2,‎ 1981, p. 167-172 (DOI 10.1093/comjnl/24.2.167).
(en) Adrian Bowyer, « Computing Dirichlet tessellations », Comput. J., vol. 24, n^o 2,‎ 1981, p. 162-166 (DOI 10.1093/comjnl/24.2.162).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.