60-graphe de Thomassen
Le 60-graphe de Thomassen est, en théorie des graphes, un graphe possédant 60 sommets et 99 arêtes. Il est hypohamiltonien, c'est-à-dire qu'il n'a pas de cycle hamiltonien mais que la suppression de n'importe lequel de ses sommets suffit à le rendre hamiltonien[1].
| 60-Graphe de Thomassen | |
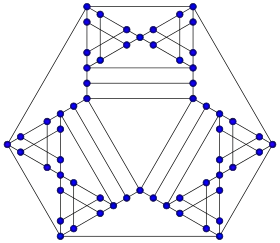 Représentation du 60-graphe de Thomassen. | |
| Nombre de sommets | 60 |
|---|---|
| Nombre d'arêtes | 99 |
| Distribution des degrés | 3 (42 sommets) 4 (18 sommets) |
| Rayon | 6 |
| Diamètre | 8 |
| Maille | 3 |
| Nombre chromatique | 3 |
| Propriétés | Hypohamiltonien |
Histoire
En 1967, Herz, Duby et Vigué conjecturent que tout graphe hypohamiltonien a une maille de 5 ou plus[2]. Cette hypothèse est invalidée en 1974 par Carsten Thomassen, qui introduit simultanément un graphe hypohamiltonien de maille 3, le 60-graphe de Thomassen, et un graphe hypohamiltonien de maille 4, le 32-graphe de Thomassen[1].
Propriétés
Propriétés générales
Le diamètre du 60-graphe de Thomassen, l'excentricité maximale de ses sommets, est 8, son rayon, l'excentricité minimale de ses sommets, est 6 et sa maille, la longueur de son plus court cycle, est 3. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Coloration
Le nombre chromatique du 60-graphe de Thomassen est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
Notes et références
- (en) Carsten Thomassen, « On hypohamiltonian graphs », Discrete Mathematics, vol. 10, 1974b, p. 383–390 (DOI 10.1016/0012-365X(74)90128-9), lien Math Reviews
- J. C. Herz, J. J. Duby et F. Vigué, « Recherche systématique des graphes hypohamiltoniens », dans Pierre Rosenstiehl, Theory of Graphs: International Symposium, Rome 1966, Paris, Gordon and Breach, , p. 153–159
Voir aussi
Lien externe
(en) Eric W. Weisstein, « Thomassen Graphs », sur MathWorld