56-graphe de Klein
Le 56-graphe de Klein ou graphe cubique de Klein est, en théorie des graphes, un graphe 3-régulier possédant 56 sommets et 84 arêtes.
| 56-graphe de Klein | |
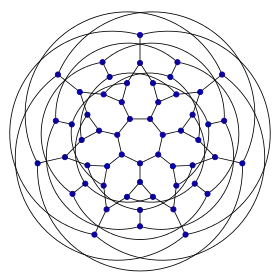
| |
| Nombre de sommets | 56 |
|---|---|
| Nombre d'arêtes | 84 |
| Distribution des degrés | 3-régulier |
| Rayon | 6 |
| Diamètre | 6 |
| Maille | 7 |
| Automorphismes | 336 |
| Nombre chromatique | 3 |
| Indice chromatique | 3 |
| Propriétés | Symétrique Cubique Hamiltonien Graphe de Cayley |
Propriétés
Propriétés générales
Le diamètre du 56-graphe de Klein, l'excentricité maximale de ses sommets, est 6, son rayon, l'excentricité minimale de ses sommets, est 6 et sa maille, la longueur de son plus court cycle, est 7. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Il peut être plongé dans une surface orientable de genre 3 qui peut être représentée comme la quartique de Klein, où il forme la « carte de Klein » à 24 faces heptagonales, de symbole de Schläfli {7,3}8.
Selon le Foster Census, le 56-graphe de Klein, référencé sous le numéro F056B, est le seul graphe cubique symétrique à 56 sommets qui ne soit pas biparti[1].
Il peut être dérivé du graphe de Coxeter à 28 sommets[2].
Coloration

Le nombre chromatique du 56-graphe de Klein est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.
L'indice chromatique du 56-graphe de Klein est 3. Il existe donc une 3-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le 56-graphe de Klein est symétrique, c'est-à-dire que son groupe d'automorphismes agit transitivement sur ses arêtes, ses sommets et ses arcs. Son groupe d'automorphisme est d'ordre 336.
Voir aussi
Crédit d'auteurs
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Klein graph » (voir la liste des auteurs).
Liens internes
Références
- (en) M. Conder et P. Dobcsányi, « Trivalent symmetric graphs up to 768 vertices », J. Combin. Math. Combin. Comput., vol. 40, , p. 41 à 63
- (en) Italo J. Dejter, « From the Coxeter Graph to the Klein Graph », Journal of Graph Theory, vol. 70, no 1, , p. 1 à 9