Verger d'Euclide

• 
  Vue de dessus ; les arbres marqués par un point bleu sont ceux qui sont visibles depuis l'origine.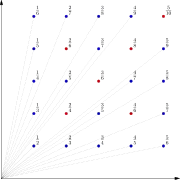
• 
  Autre vue de dessus où les arbres sont étiquetés par la coordonnée x de leur projection sur le plan x + y = 1.
• 
  Vue du verger d'Euclide en perspective centrale centrée en l'origine, dans la direction de la première bissectrice (droite d'équation y = x). Les arbres rouges sont ceux à distance « vertico-horizontale » égale à 2 de cette bissectrice.

Les arbres visibles à partir de l'origine sont ceux dont la base est un point (m, n, 0), où m et n sont premiers entre eux, c'est-à-dire tels que la fraction m/n est irréductible. L'algorithme d'Euclide, qui permet de déterminer si deux entiers sont premiers entre eux, est à l'origine de l'appellation verger d'Euclide.

Si le verger est projeté depuis l'origine sur le plan x + y = 1 (ou, de manière équivalente, dessiné en perspective à partir d'un point de vue situé à l'origine), les cimes respectives des arbres forment le graphe de la fonction de Thomae. En effet, le point (m, n, 1) se projette en

${\displaystyle \left({\frac {m}{m+n}},{\frac {n}{m+n}},{\frac {1}{m+n}}\right).}$

• Fonction de Thomae#Fonction de Thomae et verger d'Euclide
• Problème de la forêt opaque (en)

"Des fonctions monstrueuses mais utiles", article de Pour la Science.