Trivialisme
Le trivialisme (la trivialis, « trouvé partout ») est la théorie logique selon laquelle toutes les propositions sont vraies, et toutes les contradictions de la forme « p et non p » (par exemple la boule est rouge et non rouge) sont vraies. En conséquence, un trivialiste est une personne qui estime que tout est vrai[1] - [2]. En logique classique, le trivialisme est une violation directe du principe de non-contradiction d'Aristote. En philosophie, le trivialisme peut être considéré par certains comme l'opposé total du scepticisme. Les logiques paracohérentes peuvent utiliser « la loi de la non-trivialité » pour éviter le trivialisme dans les pratiques logiques qui impliquent de véritables contradictions.
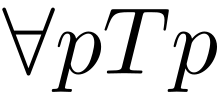
Des arguments théoriques ont été proposés pour contraster le trivialisme avec des théories telles que le réalisme modal (possibilisme), le dialétisme et les logiques paracohérentes.
Aperçu
Étymologie
Trivialisme, en tant que terme, est un dérivé du mot Latin trivialis, qui signifie que quelque chose peut se trouver partout. À partir de là, trivial a été utilisé pour suggérer quelque chose qui était introductif ou simple. En logique, à partir de cette signification, une théorie « triviale » est quelque chose considéré comme défectueux face à un phénomène complexe qui doit être complètement représenté. Ainsi, littéralement, la théorie trivialiste est quelque chose qui est exprimé de la façon la plus simple possible[3].
Théorie
En logique symbolique, le trivialisme peut être exprimé comme suit[4]:
qui serait lu comme « pour toute proposition p, p est une proposition vraie » à travers la quantification universelle (∀)
Une déclaration trivialiste peut toujours appliquer sa vérité fondamentale, aussi connu sous le nom de prédicat de vérité:
Ce qui précède serait lu comme une « proposition si et seulement si une proposition vraie », ce qui signifie que toutes les propositions sont censées être intrinsèquement prouvé comme vrai. Sans une utilisation cohérente de ce concept, une revendication de la défense du trivialisme ne peut pas être considérée comme un trivialisme authentique et complet[4].
Taxonomie des trivialismes
Luis Estrada-González dans « Models of Possiblism and Trivialism » énumère quatre types de trivialisme, à travers le concept de mondes possibles, avec un « monde » étant une possibilité et le « monde réel » étant la réalité. Il est théorisé qu'un trivialiste désigne simplement une valeur pour toutes les propositions et leurs négations comme vraies. Cette taxonomie est utilisée pour démontrer les différentes forces et plausibilité du trivialisme dans ce contexte:
- (T0) trivialisme minimale : dans un monde quelconque, toutes les propositions sont vraies et ont une valeur désignée.
- (T1) trivialisme pluraliste : dans certains mondes, toutes les propositions sont vraies et ont une valeur désignée.
- (T2) trivialisme réaliste : dans le monde réel, toutes les propositions sont vraies et ont une valeur désignée.
- (T3) trivialisme absolu : dans tous les mondes, toutes les propositions sont vraies et ont une valeur désignée[3].
Arguments contre le trivialisme
Le consensus entre la majorité des philosophes est un déni du trivialisme, appelé non-trivialisme ou anti-trivialisme[3]. Cela est dû au fait que le trivialisme est incapable de produire un argument solide à travers le principe d'explosion et de le considérer comme une absurdité (reductio ad absurdum)[2] - [4].
Aristote
Le principe de non-contradiction d'Aristote et d'autres arguments sont considérés comme étant contre le trivialisme. Luis Estrada-González dans « Models of Possiblism and Trivialism » a interprété le livre IV Métaphysique d'Aristote comme tel: «... Une famille d'arguments entre 1008a26 et 1007b12 de la forme 'Si le trivialisme est juste, alors X est le cas, mais si X est le cas, alors toutes choses sont un. Mais il est impossible que toutes choses soient un, ainsi le trivialisme est impossible.' (...) ces considérations aristotéliciennes sont le germe de pratiquement tous les suspicions subséquents contre le trivialisme: le trivialisme doit être rejeté car il identifie ce qui ne doit pas être identifié et est indésirable d'un point de vue logique, parce qu'elle identifie ce qui n'est pas identique, à savoir la vérité et le mensonge[3].
Priest
Graham Priest, professeur de philosophie, a inventé son rejet du trivialisme « la loi de la non-trivialité » comme un remplacement pour le principe de non-contradiction en logique paracohérente et dialéthéisme[5] - [6].
Arguments pour le trivialisme
Il existe des arguments théoriques en faveur du trivialisme à partir de la position de l'avocat du diable:
Argument du possibilisme
Paul Kabay a plaidé pour le trivialisme dans « On the Plenitude of Truth » parmi les suivants:
- « Le possibilisme est vrai [prémisse]
- Si le possibilisme est vrai, alors il y a un monde (possible, impossible, ou les deux), m, dans lequel le trivialisme est vrai [prémisse]
- m est un monde possible [prémisse]
- Il est vrai dans m que m est identique au monde actuel, A [2]
- S'il est vrai qu'il existe un monde, m, et m est un monde possible, et il est vrai que m est identique à A, alors le trivialisme est vrai [prémisse]
- Le trivialisme est vrai [1–5] »[2]
Ci-dessus, le possibilisme (réalisme modal, lié aux mondes possibles) est la théorie acceptée selon laquelle toute proposition est possible. Avec ce fait, le trivialisme peut être supposé vrai selon Kabay.
Implications philosophiques
Comparaison au scepticisme
Dans la comparaison de Paul Kabay du trivialisme aux écoles de scepticisme philosophique (dans « On the Plenitude of Truth »), tel que l'épicurisme, le stoïcisme et le pyrrhonisme, qui cherchent à atteindre une forme d'ataraxie ou d'état d'imperturbabilité. Une fois que tout est universellement accepté comme vrai, le trivialiste est libre de toute autre anxiété quant à savoir si tout état de fait est vrai.
Kabay compare le sceptique pyrrhonien au trivialiste figuratif et prétend que, comme le sceptique aurait atteint un état d'imperturbabilité par une suspension de croyances, le trivialiste pourrait atteindre un tel état par une abondance de croyances.
Dans ce cas—et selon des revendications de Graham Priest—le trivialisme est considéré comme l'opposé total du scepticisme[2] - [4] - [7]. Cependant, dans la mesure où le trivialiste affirme tous les états des choses comme universellement vrais, le Pyrrhoniste n'affirme et ne nie pas vérité (ou la fausseté). Le Pyrrhonisme est donc plus proche du trivialisme que le scepticisme[8].
Anti-trivialisme
_in_symbolic_logic.svg.png.webp)
(AT0) Anti-trivialisme minimal actualiste: Dans le monde réel, certaines propositions n'ont pas la valeur de vrai ou de faux.
(AT1) Anti-trivialisme absolu actualiste: Dans le monde réel, toutes les propositions n'ont pas une valeur de vrai ou faux.
(AT2) Anti-trivialisme minimal: Dans certains mondes, certaines propositions n'ont pas une valeur de vrai ou faux.
(AT3) Anti-trivialisme pointé (ou nihilisme logique minimal): Dans certains mondes, chaque proposition n'a pas de valeur de vrai ou de faux.
(AT4) Anti-trivialisme distribué: Dans chaque monde, certaines propositions n'ont pas une valeur de vrai ou de faux.
(AT5) Anti-trivialisme fort: Certaines propositions n'ont pas la valeur de vrai ou de faux dans chaque monde.
(AT6) Super anti-trivialisme (ou nihilisme logique modéré): Toutes les propositions n'ont pas une valeur vraie ou fausse dans un monde quelconque.
(AT7) Anti-trivialisme absolu (ou nihilisme logique maximal): Toutes les propositions n'ont pas la valeur de vrai ou de faux dans chaque monde[3].
Voir aussi
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Trivialism » (voir la liste des auteurs).
- (en) Graham Priest, The Many Valued and Nonmonotonic Turn in Logic, Elsevier, (ISBN 978-0-444-51623-7, lire en ligne), « Paraconsistency and Dialetheism », p. 131
- (en) Paul Kabay, On the Plenitude of Truth. A Defense of Trivialism, Lambert Academic Publishing, (ISBN 978-3-8383-5102-5)
- (en) Luis Estrada-González, « Models of Possibilism and Trivialism », Logic and Logical Philosophy, vol. 21, , p. 175–205 (lire en ligne)
- (en) Paul Kabay, « A defense of trivialism », PhD thesis, School of Philosophy, Anthropology, and Social Inquiry, The University of Melbourne, Research Collections (UMER) (consulté le ), p. 29
- (en) Graham Priest, Doubt truth to be a liar, Oxford, Oxford University Press, , 1st pbk. éd., 69–71 p. (ISBN 978-0-19-923851-4 et 0-19-923851-0)
- Graham Priest, « Perceiving contradictions », Australasian Journal of Philosophy, , Volume 77, Issue 4, p. 443 (DOI 10.1080/00048409912349211, lire en ligne)
- (en) G. Priest, « Could everything be true? », Australasian Journal of Philosophy, vol. 78, no 2, , p. 189–195 (DOI 10.1080/00048400012349471)
- Empiricus, S. (2000).
Lectures complémentaires
- (en) Frederick Kroon, The Law of Non-Contradiction: New Philosophical Essays, Oxford University Press, (ISBN 978-0-19-926517-6), « Realism and Dialetheism »
- (en) Immanuel (Immanuel), Instrumentalist Science of Zen Philosophy : Applied Ad Hoc Trivialism, Zen Applied Science, (lire en ligne)

