Triangle de Pascal (2,1)
En mathématiques, le triangle de Pascal (2,1) (ou triangle de Lucas[1]) est un tableau triangulaire d'entiers.
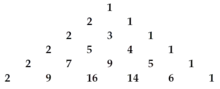
Les lignes du triangle de Pascal (2,1) — qui mises bout à bout forment la suite A029653 de l'OEIS— sont numérotées par n en commençant par n = 0 en haut. Les termes de chaque ligne sont numérotés par k en commençant par k = 0 à gauche, et sont généralement décalés par rapport aux nombres des lignes adjacentes, de sorte à former un triangle.
Ce triangle est construit par la relation de Pascal, la deuxième ligne étant (2,1) et le premier terme de chaque ligne valant 2.
Définitions
Par récurrence
Le terme d'indice k de la ligne n, noté est défini par les relations de récurrence :
pour tous entiers n et k tels que 0 < k < n, avec les initialisations :
pour , pour ; ce qui donne :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | |||||||
| 1 | 2 | 1 | ||||||
| 2 | 2 | 3 | 1 | |||||
| 3 | 2 | 5 | 4 | 1 | ||||
| 4 | 2 | 7 | 9 | 5 | 1 | |||
| 5 | 2 | 9 | 16 | 14 | 6 | 1 | ||
| 6 | 2 | 11 | 25 | 30 | 20 | 7 | 1 | |
| 7 | 2 | 13 | 36 | 55 | 50 | 27 | 8 | 1 |
Comme coefficients d'un polynôme
On montre par récurrence que se développe pour en .
Par une formule close
En écrivant , on obtient que est lié pour aux coefficients binomiaux par les formules : .
Par exemple, le coefficient central est .
Combinatoire

De même que les termes du triangle de Pascal dénombrent le nombre de chemins dans un réseau binaire, les termes du triangle de Pascal (2,1) dénombrent les chemins dans un réseau où un nœud a été rajouté (voir ci-contre).
Propriétés
Lignes
- Chaque ligne est la somme de la ligne correspondante du triangle de Pascal classique et de la ligne précédente de ce triangle.
- La somme des termes de la ligne est donc égale à (suite A003945 de l'OEIS).
- A partir de la ligne 2, la somme alternée d'une ligne est nulle, par exemple :
- ligne 3 : 2 − 3 + 1 = 0
- ligne 4 : 2 − 5 + 4 − 1 = 0
- ligne 5: 2 − 7 + 9 − 5 + 1 = 0
- Si on regarde une ligne comme la succession des chiffres décimaux d'un entier, cette ligne est "égale" à une puissance de 11 multipliée par 21 (, pour la ligne n). Ainsi, la ligne 4 : (2, 7, 9, 5, 1) devient , et la ligne 5 (2, 9, 16, 14, 6, 1) devient (après réarrangement) . Cette propriété s'explique en faisant x = 10 dans le développement de (2x + 1)(x + 1)n−1. Mais x peut aussi être une base quelconque. par exemple :
- en base 3 :
- en base 9 :
- ,
- en base 3 :
Colonnes (dans la deuxième présentation du triangle)
Chaque terme du triangle de Pascal (2,1) est la somme des termes de la colonne précédente, jusqu'au terme de la ligne précédente ; par exemple, 9 dans la ligne 4 est égal à 1 + 3 + 5. Par conséquent :
- la colonne k = 1 contient les nombres impairs dans l'ordre :
- la colonne k = 2 contient les sommes des précédents, soit les carrés :
- la colonne k = 3 contient les sommes des précédents, soit les nombres pyramidaux carrés :
- la colonne k = 4 contient les sommes des précédents, soit les nombres hyperpyramidaux carrés, suite A002415 de l'OEIS : .
Diagonales descendantes
Chaque terme du triangle de Pascal (2,1) est la somme des termes de la diagonale descendante située au dessus, jusqu'au terme situé au dessus (en ajoutant un 1 au départ de la diagonale principale) ; par exemple, 9 dans la ligne 4 est égal à 2 + 3 + 4. Par conséquent :
- la diagonale contient les entiers naturels dans l'ordre à partir de 2 :
- la diagonale contient les nombres triangulaires moins 1 :
- la diagonale donne la suite A005581 de l'OEIS décalée :
Diagonales montantes
Comme pour le triangle de Pascal classique, les sommes des termes d'une diagonale montante sont somme des sommes des deux diagonales précédentes. Cette propriété fait que tant pour le triangle de Pascal classique que pour le triangle de Pascal (2,1), les sommes des diagonales montantes forment la suite de Fibonacci avec un certain décalage. Voir les diagonales colorées ci-dessous.
1 s = 2 s = 3 2 1 s = 5 s = 8 2 3 1 s= 13 s = 21 2 5 4 1 s = 34 s = 55 2 7 9 5 1 2 9 16 14 6 1 2 11 25 30 7 1 2 13 36 55 50 27 8 1 2 15 49 91 105 77 35 9 1
Diagonales semi-descendantes
On trouve aussi la suite de Fibonacci généralisée commençant par 2 et 1, ou suite de Lucas, dans le triangle de Pascal (2,1) (d'où son appellation de triangle de Lucas) : additionner les cases de même couleur des diagonales semi-descendantes ci dessous [2].
| 1 | ||||||||
| 2 | 1 | s = 1 | ||||||
| 2 | 3 | 1 | s = 3 | |||||
| 2 | 5 | 4 | 1 | s = 4 | ||||
| 2 | 7 | 9 | 5 | 1 | s = 7 | |||
| 2 | 9 | 16 | 14 | 6 | 1 | s = 11 | ||
| 2 | 11 | 25 | 30 | 20 | 7 | 1 | s = 18 | |
| 2 | 13 | 36 | 55 | 50 | 27 | 8 | 1 | s = 29 |
| 15 | 49 | 91 | 105 | 77 | 35 | 9 | 1 |
Références
- (en) « (2,1)-Pascal triangle - OeisWiki », sur oeis.org (consulté le )
- « An Exact Value For The Fine Structure Constant. - Page 7 - Physics and Mathematics », sur Science Forums (consulté le )






























