Triangle de Nagel
En géométrie euclidienne, le triangle de Nagel d'un triangle est le triangle dont les sommets sont les points de contact des cercles exinscrits avec les côtés.
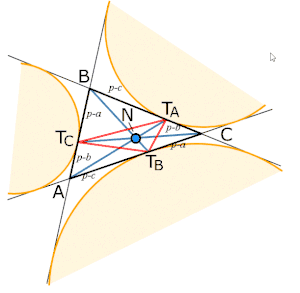
Coordonnées des sommets
Les distances des points de contact aux sommets sont indiquées sur la figure, avec les longueurs des côtés et le demi-périmètre [1].
Les coordonnées barycentriques du sommet sur le côté sont donc . On obtient les autres par permutations.
Éléments associés
Les céviennes joignant les sommets du triangle aux points de contact des cercles exinscrits avec les côtés concourent au point de Nagel [1].
De plus, elles séparent le périmètre du triangle en deux parties de même longueur égale à , d'où leur nom de séparatrices (splitter en anglais)[1].
L'ellipse tangente aux côtés du triangle aux trois sommets du triangle de Nagel est appelée ellipse de Mandart.
Aire
L'aire du triangle de Nagel est :
où S et r sont respectivement l'aire et le rayon du cercle inscrit.
Elle est égale à l'aire du triangle de Gergonne, qui, lui, a pour sommets les points de contact du cercle inscrit [2].
Références
- (en) Dov Avishalom, « The Perimetric Bisection of Triangles », Mathematics Magazine, vol. 36, no 1, , p. 60–62 (DOI 10.2307/2688140, lire en ligne).
- (en) Eric W. Weisstein, « Extouch Triangle », sur MathWorld



![[BC]](https://img.franco.wiki/i/fd2ee765006b05ac0001c01a206871306f108cbc.svg)


