Traitement des données Doppler pulsées

Un radar Doppler pulsé émet des impulsions cohérentes par une antenne ou un transducteur. Celles-ci sont superposées à la fréquence porteuse du signal radar. Entre chaque impulsion, l'antenne et le circuit électronique sont mis à l’écoute de l’impulsion de retour. On calcule la distance entre le radar et les précipitations par la relation suivante (le facteur ½ tient compte que t correspond au temps d'aller-retour du signal) :

${\displaystyle {\text{Distance}}=c\ {\frac {\Delta t}{2}}}$ (c = vitesse de la lumière = 299 792,458 km/s).

La distance maximale qu'on peut sonder sans ambiguïté dépend du ${\displaystyle \scriptstyle \,\Delta t}$ utilisé entre deux impulsions subséquentes. En effet, la position de tout retour qui arrive d'une première impulsion, après qu'une seconde impulsion est partie, sera mal interprétée comme revenant de cette dernière. Selon la vitesse de rotation de cette dernière et la fréquence de répétition des impulsions (FRI), il peut y avoir des dizaines d'impulsions reçues et retournées par la cible.

Les radars Doppler pulsés modernes possèdent un étage de démodulation du signal entrant qui centre la fréquence sur zéro, en retirant la fréquence porteuse, avant l'échantillonnage numérique des échos. Le signal résultant contient non seulement l'intensité de l'écho mais aussi la variation de la fréquence causée par l'effet Doppler d'une cible s'éloignant ou se rapprochant du radar. La donnée de l'écho est souvent appelé IQ-data où IQ signifie « en phase » et « en quadrature de phase » pour rappeler que le signal est représenté par un nombre complexe avec une partie réelle et une partie imaginaire.

Par exemple, un signal modulé ${\displaystyle S(t)=A\cos(\omega _{0}t+\phi (t))}$ pourra être démodulé en utilisant :

${\displaystyle IH(t)=S(t).\cos(\omega _{0}t)}$ et ${\displaystyle QH(t)=S(t).\sin(\omega _{0}t)}$

En utilisant un filtre passe-bas à la fois sur IH(t) et QH(t) on obtiendrait[1] :

${\displaystyle I(t)=\cos(\phi (t)+\Phi )}$
${\displaystyle Q(t)=\sin(\phi (t)+\Phi )}$

Où :

• ${\displaystyle \phi (t)}$ est le changement de phase entre le signal émis et celui reçu d'une même distance ;
• ${\displaystyle \omega _{0}}$ est la vitesse angulaire du signal de base ;
• ${\displaystyle A^{2}=I^{2}+Q^{2}}$ est l'intensité du signal (l'amplitude au carré).

Échantillonnage

Le traitement du signal commence par un échantillonnage.

Traitement des valeurs de I and Q dans une des cases spécifiques d'échantillonnage.

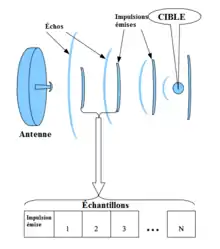
Entre chaque impulsion, le processeur radar fait un échantillonnage du signal retourné au radar. Dans le diagramme à droite, la partie du haut montre l'évolution du front d'onde reçu par l'antenne et provenant d'une cible à une même gamme de distances lors d'une succession d'impulsions. Le front d'onde donne un motif d'évolution en spirale avec le temps. Chacun de ces échantillons est séparé par période d'émission (1/FRI).

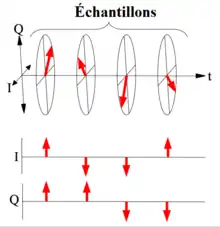
Le signal de l'oscillateur local du radar, qui sert à synchroniser l'émission des impulsions, est divisé en deux signaux qui sont décalés de 90 degrés et mélangés aux signaux reçus, et chacun va vers les deux détecteurs différents en même temps que le signal de réception. Ceci donne dans un détecteur la valeur de I (t) et dans l'autre produit Q (t) de la partie du bas où I correspond à l'intensité du signal à Q, la phase de réception[1].

Si la cible à cette distance était immobile, I et Q seraient les mêmes, quelle que soit l'impulsion utilisée, et la différence entre leurs valeurs successives serait nulle. Le diagramme montre une spirale dans le sens antihoraire, ce qui correspond à un mouvement vers le radar. Un mouvement s'éloignant du radar produirait une spirale dans le sens horaire.

Analyse de Fourier du spectre de puissance du signal dans une case d'échantillonnage versus la vitesse radiale des cibles qui sont présentes dans l'échantillon.

Relation entre la largeur du spectre Doppler (W), montré par les flèches, et la distribution des vitesses dans les échantillons.

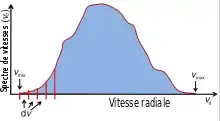
Habituellement, de nombreuses cibles sont présentes dans le volume de l'échantillon radar. Chacune des cibles individuelles produit un décalage de fréquence en fonction de sa vitesse radiale ce qui fait que ${\displaystyle {\texttt {I}}}$ et ${\displaystyle {\texttt {Q}}}$ ne varie pas d'une façon aussi régulière qu'il serait attendu pour une cible unique. En faisant une transformée de Fourier discrète du signal discret ${\displaystyle z[t]}$, il est possible d'obtenir la variation de la puissance renvoyée dans un intervalle de décalage fréquentiel (spectre Doppler) et donc la variation de vitesse entre les différentes cibles à la distance d'où reviennent les impulsions[2] - [3]. Ceci est illustré sur la figure à droite, où un schéma de spectre Doppler est affiché. La fréquence est déjà convertie en vitesse radiale ${\displaystyle v_{d}}$ dans l'axe des abscisses. À partir du spectre Doppler, la réflectivité (${\displaystyle Z}$) peut être calculée en utilisant l'expression:

$${\displaystyle Z=\int _{v_{\min }}^{v_{\max }}{\widehat {\Gamma }}_{z,z}dv_{d}}$$

L'intégrale de la puissance spectrale (soit la transformé de Fourier de la fonction d'autocorrélation) est appelée le moment zéro du spectre Doppler, ce qui équivaut à la réflectivité (${\displaystyle Z}$). En outre, le premier moment donne la vitesse ${\displaystyle V}$ et le deuxième le spectre Doppler[3] :

$${\displaystyle V={\frac {1}{Z}}\int _{v_{min}}^{v_{max}}v_{d}{\widehat {\Gamma }}_{z,z}dv_{d}\quad ,\quad W={\sqrt {{\frac {1}{Z}}\int _{v_{min}}^{v_{max}}(v_{d}-V)^{2}{\widehat {\Gamma }}_{z,z}dv_{d}}}}$$

${\displaystyle V}$ est la vitesse Doppler moyenne correspondant à la vitesse radiale moyenne des cibles dans le signal discret ${\displaystyle z[t]}$. Dans le cas de détection aérienne, cette vitesse peut masquer la vitesse réelle de nombreux aéronefs (avions, hélicoptères, etc.) évoluant à proximité l'un de l'autre. Pour un radar météorologique, elle correspond à la vitesse moyenne des hydrométéores dans l'échantillon. Elle peut également être influencée fortement par les échos revenant du sol qui ont une vitesse nulle par définition.

Le deuxième moment, la largeur Doppler (${\displaystyle W}$), correspond à la variance du spectre Doppler. Il peut être une mesure du nombre de modes la distribution de la taille des cibles. Une distribution de mono-modale (un seul pic) est le plus souvent associée à un seul aéronef en détection aérienne ou à un seul type d'hydrométéores en météorologie. Une distribution qui a plusieurs modes (plusieurs pics) correspond par contre à la présence de plusieurs aéronefs ou à un mélange de précipitations. La largeur de la distribution dans le cas du radar météorologique indique la présence ou non de turbulence atmosphérique (large spectre)[3].