Théorème de la corde universelle
En mathématiques, et plus précisément en analyse, le théorème de la corde universelle, ou théorème des cordes universelles, dû à Paul Lévy[1], décrit dans sa version générale une propriété des courbes planes continues joignant un point à un point ; il répond à la question de savoir si on peut trouver sur cet arc des points et tels que la corde ait une longueur donnée et soit parallèle à la corde . Le théorème affirme que cette corde existe pour tout arc joignant à si et seulement si la longueur est un diviseur entier de la longueur (pour un arc particulier, il existe en général d'autres cas d'existence de la corde , comme dans l'exemple ci-contre. L'expression « corde universelle » signifie que le résultat s'applique à un arc quelconque).
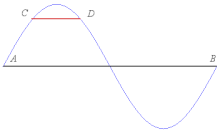
Historique
Une forme équivalente de la partie directe du théorème a été obtenue par André-Marie Ampère dans le cadre de travaux sur le théorème de Taylor en 1806[2]. Les versions actuelles du théorème et de sa réciproque, présentées comme une généralisation du théorème de Rolle, ont été publiées par Paul Lévy en 1934[1].
Version fonctionnelle horizontale
Énoncé
Considérons une fonction réelle continue sur , , telle que : le théorème direct affirme que pour tout entier , il existe un tel que ; le théorème réciproque stipule que les nombres sont les seuls réels assurant l'existence d'un réel vérifiant pour toute fonction .
Notons que dans ce cas le rôle des points du cas général est joué par les points et que les cordes et sont horizontales.
Démonstration du théorème direct
On introduit la fonction qui est continue sur ; la somme télescopique vaut , ce qui montre que les ne sont pas tous de même signe, et donc (d’après le théorème des valeurs intermédiaires) que s’annule sur , ce qui assure l'existence d'un tel que .
Réciproque : contre-exemple de Paul Lévy
En prenant, sans perte de généralité[alpha 1], , ; Lévy propose de considérer la fonction où est une fonction continue sur périodique de plus petite période strictement positive et vérifiant , sur ; par exemple . est bien continue sur et vérifie et un calcul direct montre que , qui ne s'annule que si avec entier. Si donc on choisit différent de l'inverse d'un entier, on construit bien un exemple où il n'existe pas de vérifiant .
Version fonctionnelle oblique
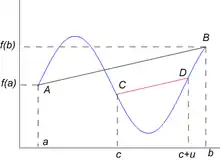
Énoncé
On considère toujours une fonction réelle continue sur , : le théorème direct affirme que pour tout entier , il existe un tel que le taux d'accroissement de entre et est égal à celui entre et : ; le théorème réciproque stipule que les nombres sont les seuls réels assurant l'existence d'un réel vérifiant , pour toute fonction .
Ici aussi les rôles des points sont joués par les points .
Démonstration
Il suffit d'appliquer le théorème précédent à la fonction définie par , qui vérifie .
Lien avec le théorème des accroissements finis
Dans le cas dérivable, le taux d’accroissement est, pour grand, une approximation de la dérivée , si bien que la formule "tend" vers la formule des accroissements finis (mais on ne peut déduire l'un de l'autre car le réel dépend de ).
Interprétation cinématique
Considérons un mobile animé d'un mouvement continu parcourant une distance en un temps et dénommons la distance parcourue en fonction du temps (avec ). Les taux d'accroissements s'interprètent alors comme des vitesses moyennes, et le théorème précédent s'énonce comme suit : on est assuré de l'existence d'un intervalle de temps durant lequel la vitesse moyenne du mobile est égale à la vitesse moyenne globale si et seulement si est entier. Ce résultat a été popularisé par les exemples suivants.
Le paradoxe du coureur
Si un coureur parcourt 10 kilomètres en 30 minutes[alpha 2], il paraît vraisemblable qu’il y ait au moins un kilomètre de son trajet qu’il a couru en 3 minutes exactement. Le résultat de Lévy montre que cela n’est garanti que si la course complète est un nombre entier de kilomètres[3].
Le paradoxe du train
Un train parcourt un certain trajet à une vitesse moyenne de 100 km/h. La durée du trajet, en heures, est égale à (nombre réel positif). Pour quelles valeurs de peut-on être certain qu’il existe durant le trajet deux points distants de 100 km que le train a parcouru en un laps de temps de une heure ?
Réponse : uniquement pour entier.
Version concernant les courbes paramétrées planes
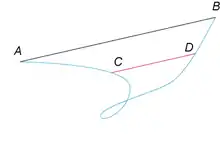
Énoncé
On considère deux fonctions fonction et réelles continues sur ; alors, les seuls réels pour lesquels on est assuré de l'existence de tel que le déterminant soit nul sont les avec entier.
Si l'on pose , le théorème énonce bien les conditions d'existence pour les courbes paramétrées joignant à d'une corde parallèle à , le déterminant nul indiquant la colinéarité des vecteurs et .
Notons que ce théorème contient les deux précédents.
Démonstration
Appliquer le théorème de base à la fonction définie par qui vérifie . L'égalité équivaut bien la nullité de par linéarité du déterminant par rapport à sa première colonne.
Version concernant les courbes paramétrées dans l'espace
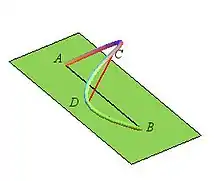
Énoncé
On considère trois fonctions fonction réelles continues sur ; alors, les seuls réels pour lesquels on est assuré de l'existence de tel que le déterminant soit nul sont les avec entier.
Si l'on pose , le théorème énonce les conditions d'existence pour les courbes paramétrées joignant à d'une corde parallèle au plan , le déterminant nul indiquant la colinéarité des vecteurs , et .
Le point pouvant être choisi arbitrairement, il énonce en fait les conditions d'existence d'une corde parallèle à un plan donné passant par et . Par contre, comme on le voit ci-contre, la généralisation qui consisterait à dire qu'il existe une corde parallèle à est fausse.
Notons que ce théorème contient les trois précédents.
Démonstration
Appliquer le théorème de base à la fonction définie par qui vérifie . L'égalité équivaut bien à la nullité de par linéarité du déterminant par rapport à sa première colonne.
Cas d'une fonction continue sur ℝ

Énoncé
Soit une fonction réelle continue sur ; il suffit que atteigne sa borne inférieure ou supérieure pour être assuré, cette fois pour tout réel , de l'existence d'un réel vérifiant (appelé parfois théorème des cordes horizontales).
Démonstration
Supposons que et posons ; alors et , d'où l'existence d'un tel que .
D'après le théorème des bornes atteintes, la condition sur la fonction est réalisée pour une fonction continue périodique sur , ou une fonction ayant des limites égales aux deux infinis.
Voir ici [4] une généralisation au cas de fonctions non continues.
Une application physique
A tout point d'un cercle de diamètre de longueur , on fait correspondre une grandeur physique (disons par exemple la température) qui varie continûment sur le cercle ; alors pour tout le cercle possède forcément une corde de longueur dont les extrémités sont à même température (paramétrer le cercle par un angle et considérer la fonction qui à fait correspondre la température en ).
Variante pour une fonction continue sur un segment
Énoncé
Soit une fonction réelle continue sur , , telle que , et soient tels que . Alors, sans autre condition sur , il existe toujours tel que ou tel que .
Démonstration
Considérons la fonction continue périodique de période sur prolongeant ; d'après le théorème précédent, il existe un réel tel que et d'après la périodicité, on peut supposer que ; si , c'est gagné. Sinon, donc . Donc si on pose , .
Illustration cinématique
Un train parcourt 500 km en 5 h.
1) Existe-t-il forcément deux points distants de 100 km, joints en un laps de temps de 1 h ?
2) Existe-t-il forcément deux points distants de 200 km, joints en un laps de temps de 2 h ?
3) Existe-t-il forcément deux points distants de 300 km, joints en un laps de temps de 3 h ?
Réponses : oui pour 1) car 100 divise 500, non pour 2) et non pour 3) car ni 200 ni 300 ne divisent 500, mais oui pour 2) ou 3) d'après l'énoncé précédent.
Généralisation à des parties du plan
En 1937, Hopf généralisa ces résultats aux sous-ensembles compacts et connexes du plan [5].
Voir aussi
Articles connexes
Notes et références
Notes
- Il suffit d’utiliser le changement de variable .
- Le record du monde du 10 000 mètres est en 2019 de 26 min 17 s 53 (depuis 2005).
Références
- Paul Lévy, Sur une généralisation du théorème de Rolle, C. R. Acad. Sci., Paris, 198 (1934) 424–425.
- André-Marie Ampère, Recherches sur quelques points de la théorie des fonctions dérivées qui conduisent à une nouvelle démonstration de la série de Taylor, et à l’expression finie des termes qu’on néglige lorsqu’on arrête cette série à un terme quelconque. J. Ecole Polytechnique 6 (1806), no. 13, pp. 148-181 (lire en ligne).
- (en) Le paradoxe du coureur, sur le site math.hawaii.edu.
- (en) J.C. Oxtoby, « Horizontal Chord Theorems », The American Mathematical Monthly, vol. 79, , p. 468–475
- (de) Heinz Hopf, « Über die Sehnen ebener Kontinuen und die Schleifen geschlossener Wege. », sur E-Periodica (consulté le )
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Universal chord theorem » (voir la liste des auteurs).




![{\displaystyle [CD]}](https://img.franco.wiki/i/cc0573d2a8fc2386767a2b81c2a5777e9271ae59.svg)
![[AB]](https://img.franco.wiki/i/13e80b9404482bdbe7fe18d8435b3dd42fd39bb0.svg)




![[a,b]](https://img.franco.wiki/i/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)



![{\displaystyle c\in \left[a,b-{\frac {b-a}{n}}\right]}](https://img.franco.wiki/i/de960833e65d9d0c4893e36cad9cf245d84faf68.svg)








![{\displaystyle \left[a,b-{\frac {b-a}{n}}\right]}](https://img.franco.wiki/i/389d5b921699632b3264678c69ac40e5e193e4dd.svg)












![{\displaystyle ]0,T[}](https://img.franco.wiki/i/4873c017bacfee52473336a3e26a935ebc24cd42.svg)

![[0,1]](https://img.franco.wiki/i/738f7d23bb2d9642bab520020873cccbef49768d.svg)



















![{\displaystyle t\in [t_{0},t_{0}+T]}](https://img.franco.wiki/i/37ae0dee3147da9f5f4d941f10565eb3dca6d7b8.svg)
![{\displaystyle [t_{1},t_{2}]}](https://img.franco.wiki/i/6e35e13fa8221f864808f15cafa3d1467b5d78ce.svg)



![{\displaystyle c\in \left[a,b-u\right]}](https://img.franco.wiki/i/bbf86367db5f9da530f0ba17e57e5983c79b4eed.svg)





























![{\displaystyle c\in \left[a,b-v\right]}](https://img.franco.wiki/i/a3a7ad82e3f4845780beded8abd229800270bb7a.svg)



![{\displaystyle c\in \left[a,b\right]}](https://img.franco.wiki/i/b48d674e0c628e1da26f4ca2f6b1079842954555.svg)
![{\displaystyle c+u\in \left[a,b\right]}](https://img.franco.wiki/i/cd67e5b5fee384f7316230cf5535b3840ba862a0.svg)





